基于多模态快速非奇异终端滑模的船舶航迹跟踪自抗扰控制
郭 杰, 刘轶华, 马利华
(上海海事大学 商船学院, 上海 201306)
欠驱动船舶系统是指控制其运动系统的输入量少于其需要控制的运动自由度的数量[1],具有船舶运动模型参数不确定和非线性强等特点,加上外界风、浪、流的干扰,航迹控制器设计比较困难。常规船舶上只安装有螺旋桨主推进器和舵装置,是典型的欠驱动船舶系统。[2]传统非完整系统的控制方法并不能直接应用到此类系统中。因此,对这类问题进行研究有重要意义。[3]
国内外学者对航迹控制问题已有丰富的研究成果。文献[4]~文献[6]设计控制器的基础均为精确的数学模型,因此当参数辨识不精确时难以应用。滑模控制(Sliding Mode Control,SMC)因具有对参数摄动的不变性而引起广泛关注。传统的滑模是一种线性滑模,如果需要较大的收敛速率,必须增大控制增益,而这会引发输入饱和现象。为克服线性滑模渐进稳定的问题,文献[7]提出终端滑模(Terminal Sliding Mode,TSM)的控制策略,由于传统TSM存在奇异问题,进而提出非奇异终端滑模(Nonsingular Terminal Sliding Mode,NTSM)控制。文献[8]采用NTSM控制,在模型参数不确定的情况下实现航迹控制,对外界风、流、浪的干扰有较好的抵抗作用。文献[9]设计的滑模面虽能弥补普通TSM的缺点,但其收敛速度不够理想。文献[10]提出自抗扰控制(Active Disturbance Rejection Control,ADRC)技术有不依赖精确模型的优良控制特性。文献[11]提出非线性扩张状态观测器(Nonlinear Extended States Observer,NLESO),在一定范围内,对不确定系统有很好的跟踪性能。但是,目前还没有针对其中非线性函数选择的明确理论依据,在大多数情况下还是要依靠研究者的经验判断。由于NLESO在参数整定不易、稳定性分析和控制性能分析等方面有一定困难,为扩大扩张状态观测器(Extended States Observer,ESO)的应用,文献[12]将其中的非线性函数替换为线性函数,从而得到线性扩张状态观测器(Linear Extended States Observer,LESO),具有参数整定方便和理论分析简单等优点,且对扰动的抵抗性能较强。文献[13]得出LESO的观测精度较低的结论。文献[14]提出当系统模型未知时,LESO的观测误差收敛是有一定条件的。
本文对原本的ESO进行改造,实时在线性函数与非线性函数之间切换,进而设计一种可切换的组合式ESO,同时发挥两种函数的优点,使其性能在不依赖于精确的数学模型的基础上得到进一步提升。同时,基于多模态的思想,采用分段切换函数设计NTSM,根据实际情况选择适当的滑模面,实现多个滑动模态,并引入一种新型双幂次趋近律,以期达到快速趋近的目的。此外,将此趋近律和NTSM引入状态误差反馈(States Errors Feedback,SEF)环节,设计的基于多模态的快速NTSM在继承原本ADRC优良控制品质的同时,能提高收敛速度和精度,改善控制器性能。
1 船舶运动数学模型
三自由度欠驱动水面船舶运动模型[15]为
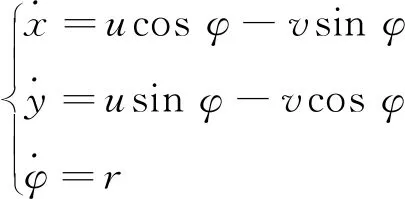
(1)
式(1)中:x、y和φ分别为船舶在坐标系下的坐标位置和艏向角;u、v和r分别为纵向速度和横荡速度、艏向角速度。考虑ADRC的设计,加上控制过程中非线性因素和外界干扰的影响,可得出
(2)
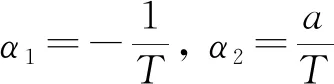
(3)
式(3)中:δr为命令舵角;KE为舵机控制增益;TE为舵机时间常数。
由上述计算可得运动数学模型为
(4)
2 基于FNTSM的ADRC设计
2.1 FNTSM算法
由文献[8]可知,传统TSM的切换函数为
(5)
式(5)中:x1和x2为系统状态变量;β>0;p和q为正奇数,且p=2m+1,(m=1,2,…),p>q。对应的控制律为
(6)
此控制律在x1=0、x2≠0时存在奇异问题,特别是在平衡点附近出现的频率很高,奇异现象严重。
为克服TSM的奇异问题,研究者设计了很多切换函数,其中文献[8]中NTSM切换函数为
(7)
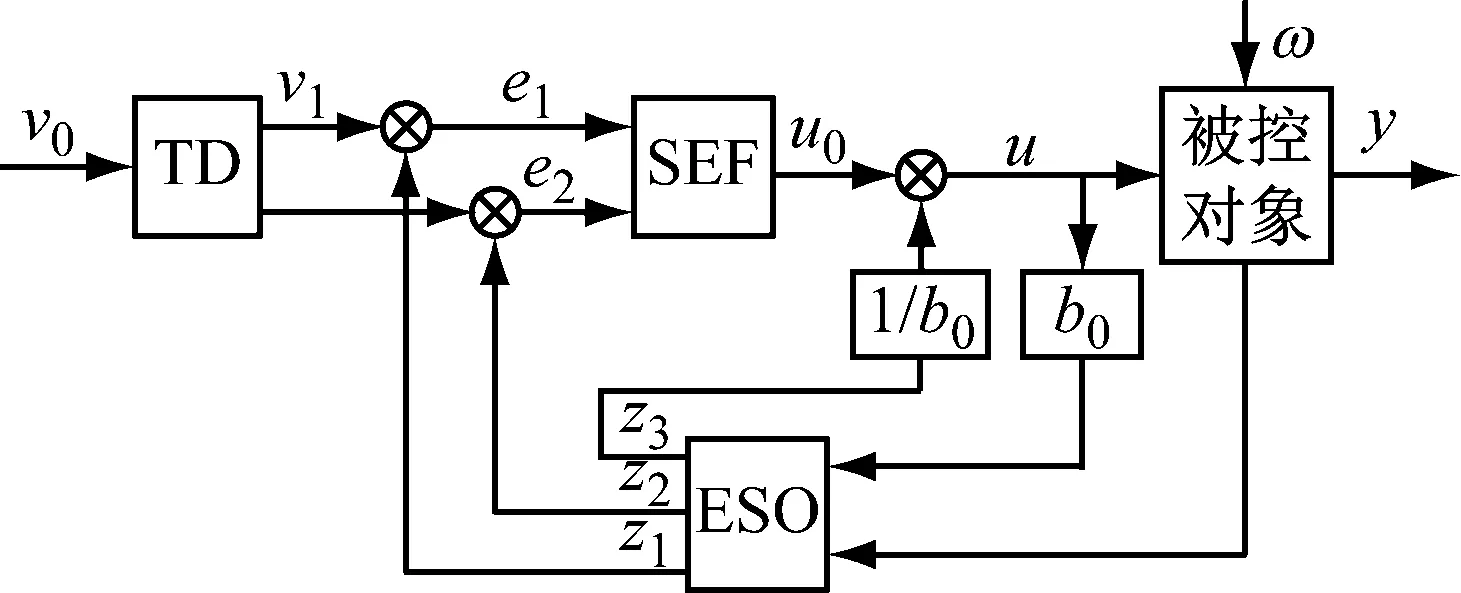
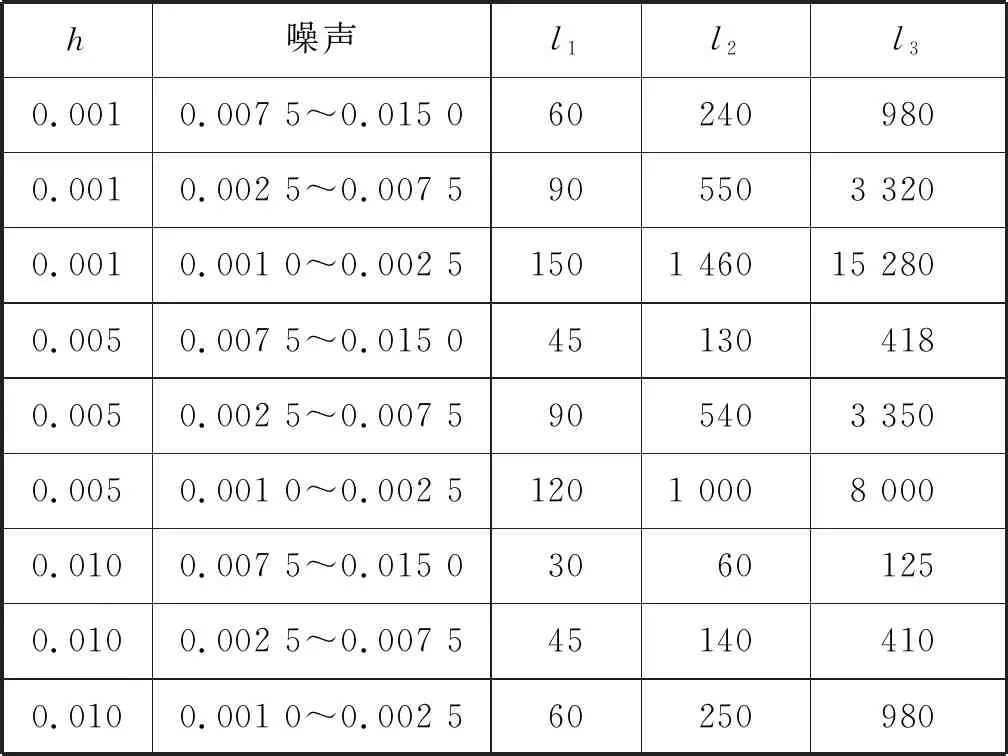
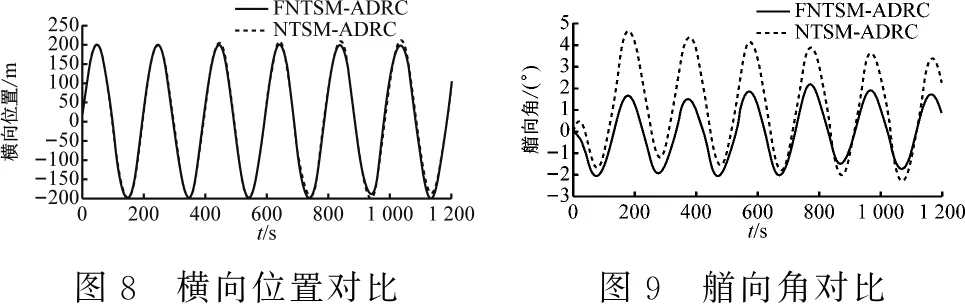
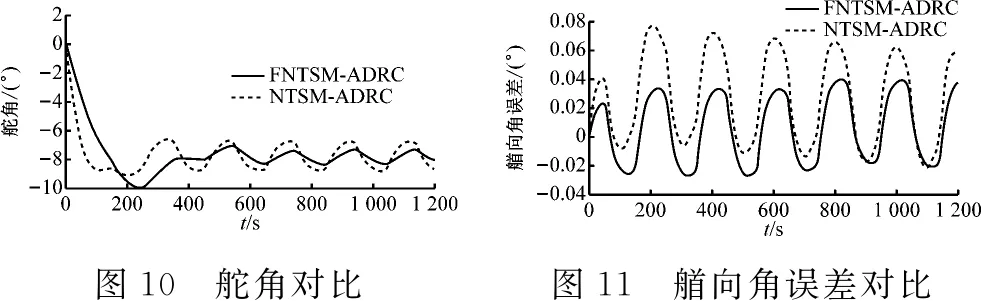
式(7)中:x1和x2为系统状态变量;β和v为可调参数,β>0,1 为进一步改善收敛性能,本文基于多模态的思想设计一种组合式的滑模面,可根据实际情况进行选择,并引入一种新型的双幂次趋近律,得到快速非奇异终端滑模,提高收敛速度。本文设计的分段切换函数[17]为 (8) s2=x2+β1/vsgn(x1)|x1|ω (9) 式(8)中:ω为可调参数,且ω>1。当|x1|<1时,取切换函数s1=0;当|x1|≥1时,取切换函数s2=0。两切换函数收敛度对比见图1。 图1 两切换函数收敛度对比 由图1可知:当|x1|<1时,切换函数s1的收敛速度优于s2;当|x1|≥1时,s2的收敛速度大大优于s1。因此,采用切换设计可同时发挥两个函数的优点。 本文采用的新型双幂次趋近律相比传统的趋近律,具有更好的运动品质。[18]推导分段切换函数相对应的控制律[19]过程如下。 根据式(4)定义船舶航向误差为 φe=φ-φd (10) 式(10)中:φd为指令信号,即期望航向。 (11) 令 f(r)=-α1r-α2r3 (12) 由此可得二阶船舶航向控制系统为 (13) 由式(8)和式(9)结合船舶系统可得 (14) (15) 对式(13)进行求导可得 (16) (17) 可得 sgn(s1)-k2|s1|βsgn(s1) (18) 整理得控制律为 (19) 对未知的外界干扰ω(t)进行限制,‖ω(t)‖ (20) 式(20)中:η为设计常数。同理可得切换函数s2对应的控制律为 (21) 当|x1|<1时,取控制律u1;当|x1|≥1时,取控制律u2。对于式(13),分别取式(14)和式(20)、式(18)和式(21)时,能使得在有限时间内,系统状态变量最终到达终端滑模面,且跟踪误差收敛到0,此证明过程可详见文献[8]。 韩京清[10]利用非线性机制开发一些具有特殊功能的环节,如跟踪微分器(Tracking-Differentiator,TD)和扩张状态观测器等,并加以组合,由此形成自抗扰控制技术。该技术因具有良好的控制特性而备受关注,此后随着研究深入,出现许多富有成效的研究成果。[20]二阶不确定非线性系统ADRC结构见图2。[21] 图2 二阶不确定非线性系统ADRC结构图 2.2.1TD 采用二阶最速跟踪微分器能更快地实现对输入信号及其微分的跟踪。结合式(13)可得其离散算法[22]为 (22) 式(22)中:φd(k)为输入信号;φd1(k)和φd2(k)分别为φd(k)的跟踪信号和近似微分信号;r0为速度因数;h为滤波因数;T为系统积分步长;fhan(φd1,φd2,r0,h)为最速控制综合函数,其计算式见文献[10]。 2.2.2LESO和NLESO切换法 抖振问题是滑模控制方法的固有缺陷,当控制系统有较大不确定性时,为保证系统的鲁棒性,控制量的抖振现象会更严重,解决系统的不确定性问题成为关键。ESO理论的出现为处理不确定性问题提供了新的方式,ESO为ADRC的核心部分,其作用是根据输入和输出数据对系统动态和总扰动进行实时估计,可根据函数类型的不同分为线性扩张状态测器和非线性扩张状态观测器。相对应的ADRC分为线性自抗扰控制(Linear Active Disturbance Rejection Controller,LADRC)[23]和非线性自抗扰控制(Nonlinear Active Disturbance Rejection Controller,NLADRC)。[24] LESO的理论分析较为简单,参数整定方便,且跟踪性能几乎不随扰动幅度的变化而变化;NLESO相对来说较为困难和复杂,跟踪性能与扰动幅度有关。但是,采用本文所述方法可使得其与LESO有同等噪声放大效应,同时具有参数效率较高和跟踪精度高等优点。由此可知:LESO和NLESO的特点不同,为发挥各自的优势,采用组合方式设计ESO[25],即 (23) (24) 式(23)和式(24)中:e1=z1-y,z1为y的跟踪信号;z2为z1的微分信号;z3为总扰动的跟踪信号;li为ESO的增益函数;b0为b的估计值;gi(e1)为一种常用的非线性函数。设置切换条件如下:当ESO跟踪偏差|e1|>1时,采用LESO,即式(23);反之,采用NLESO,即式(24)。这样就能发挥各自的优点。gi(e1)的表达式为 (25) 式(25)中:αi和δ为待定常数。 (26) 令gi(e1)=λ0i(e1)e1,取αi=0.25,δ=0.05,分析λ0i(e1)函数的特性曲线见图3。 图3 λ0i(e1)函数特性曲线 由图3可知:λ0i(e1)在线性区间δ内是常数,当误差e1>δ时,随着误差的增大而减小,具有“大误差,小增益;小误差,大增益”的特点,因此,将|e1|>1作为切换条件是合适的。 2.2.3参数整定 “不退不改”“只改不退”……当前,电影票“退改签难”问题广泛存在。记者调查发现,不同售票渠道“退改签”标准不一,套路重重,饱受消费者诟病。近日,中国电影发行放映协会发布《关于电影票“退改签”规定的通知》,要求电影票“退改签”规定要优化流程、简化手续,并尽快实施,维护消费者权益。 LESO的参数整定问题可通过文献[12]中的“带宽法”或其改进型来解决,难点在于NLESO的参数整定问题。本文采用一种结合“带宽法”和“经验法”的较为适于调试的参数整定方法,原则如下: (2) 由图3可知:δ的取值过大会导致丢失非线性增益的优势,过小会导致系统不稳定,一般取δ=0.01;αi通常取经验值,α1=1,α2=0.5,α3=0.25。 (3) 在切换控制中,当扰动幅度较大时采用LESO,当扰动幅度较小时采用NLESO;根据文献[25]得到δ=0.01时,典型三阶ESO参数和NLESO的参数设置可参考表1。 2.2.4稳定性分析 针对此切换型ESO进行简单且便于应用的稳定性分析。典型三阶NLESO的表达式为 表1 参数优化表 (27) 令 g2(e1)=λ02(e1)e1 (28) g3(e1)=λ03(e1)e1 (29) 将式(28)和式(29)代入式(27),可得 (30) (31) (32) (33) 采用传递函数形式和根轨迹法分析如下: 根据劳伦斯判据,该ESO稳定的充要条件为 λ02l1l2>λ03l3 (34) 若α2=α3,则λ02=λ03,满足l1l2>l3即可。对于切换型ESO,只要满足 (35) (36) 2.2.5SEF 利用ESO能够实时获得总扰动估计值的特性,在控制律中给予补偿,由此实现自抗扰控制。误差反馈控制律为 (37) 式(37)中:u0为基于多模态思想设计的分段滑模控制律,即 (38) 通过期望艏向角方程将航迹控制问题转化为航向控制问题[1],有 (39) 式(39)中:β0用于压缩航迹偏差坐标;β1用于调整航迹收敛速度;β2用于调整积分速度。将式(39)中的φd(t)作为ADRC的参考输入信号,使艏向角跟踪φd(t),有 (40) 计划航迹向φp=0°,计划航迹yp=0,航迹偏差Δy=500 m,此处只仿真分析横向航迹偏差,因为纵向航迹偏差可通过螺旋桨来控制,前进速度u=7 m/s,初始航向φ=0°。横向航迹偏差、艏向角、舵角和艏向角误差的变化曲线分别见图4、图5、图6和图7。 计划航迹向φp=0°,计划航迹yp=200sin(0.000 4πx),前进速度u=7 m/s,v=0.3 m/s,初始航向φ=0°。横向位置、艏向角、舵角和艏向角误差的变化曲线分别见图8、图9、图10和图11。 在上述直线航迹控制仿真中,设计的FNTSM-ADRC相较于NTSM-ADRC,横向航迹摇摆程度较小,且更早地到达偏差为0的位置;在曲线航迹控制中,FNTSM-ADRC相较于NTSM-ADRC航迹更贴近于振幅为200的正弦曲线,且在两种情形中为达到期望航迹所调整的舵角、艏向角幅度均相对较小,有利于减少反复操作和舵机磨损。由图10和图11可知:在直线和曲线航迹控制中,FNTSM-ADRC相较于NTSM-ADRC艏向角误差均较小。由上述分析可知,本文设计的航迹控制器相对来说收敛速度快,精度高,效果好。 本文针对欠驱动水面船舶航迹控制问题,在原有ADRC的基础上,对扩张状态观测器采用组合式函数设计进行改造,并将基于多模态思想构造的NTSM和一种新型的双幂次趋近律引入状态误差反馈环节中,达到快速趋近的效果。同时,构建期望艏向角方程,产生控制系统的期望输入,从而达到航迹控制的目的。本文分别设计了直线和曲线航迹控制两种情况下的仿真试验,结果表明:设计的新型控制器相对来说能更好地提高收敛速度和控制精度,有较好的控制特性。在后续的工作中,将继续研究如何在更加复杂的海况下做到精准控制。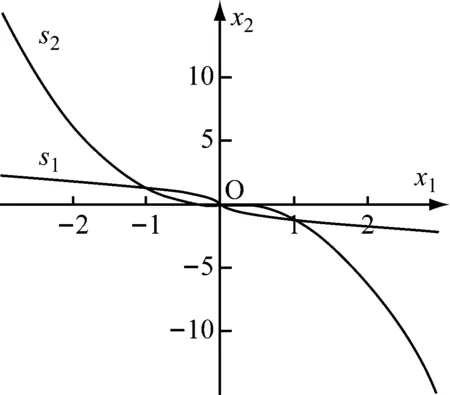



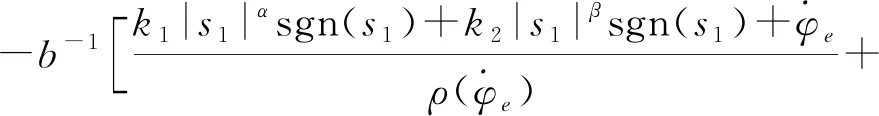
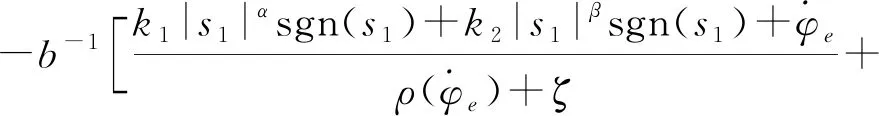
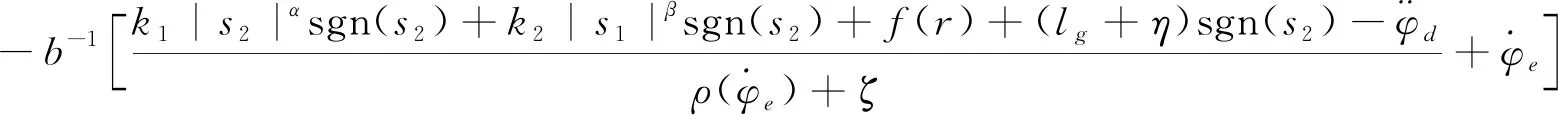
2.2 自抗扰控制方法
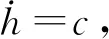


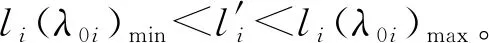
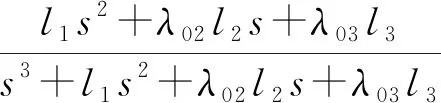
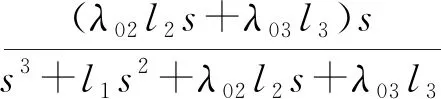

3 风、流影响下的航迹控制方法与Simulink仿真

3.1 直线航迹控制

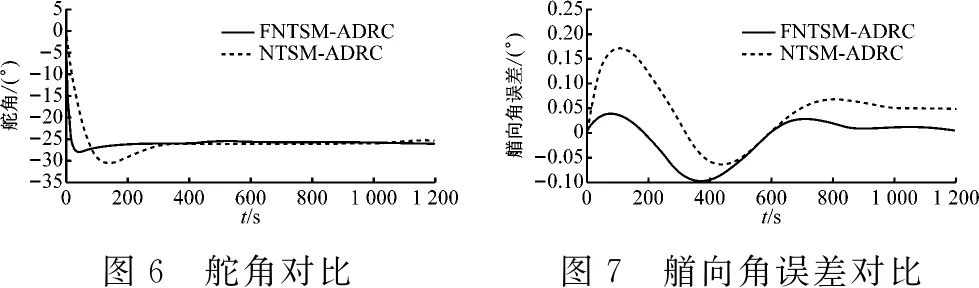
3.2 曲线航迹控制
4 结束语

