圆锥曲线中范围问题的求解策略

魏成年

(甘肃省武威第六中学 733000)

圆锥曲线中的取值范围问题是高考的热点，也是高考的难点.从学生的答题情况看，相当多的毛病出在运算上，究其原因，往往是方法选择不当或运算不合理(策略意识差)，造成中途搁浅或结果出错.问题的根源在于学生解题不讲策略，遇到题目瞎撞乱碰，而运算时也缺乏目标意识，不讲究运算的合理性.因此，如何增强圆锥曲线的解题策略意识，提高运算的速度和准确度就显得尤为重要.下面我们以近年的高考题为例来说明解决这类问题的策略方法.

一、利用圆锥曲线的几何性质构造不等关系来确定参数的取值范围

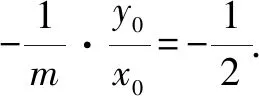
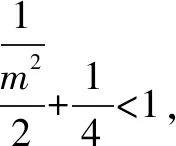
(2)解法略.

评析有关中点弦的问题，利用点差法：设点代入→作差→斜率关系，可以减少运算、降低难度，为解题带来方便.

二、利用圆锥曲线中的判别式构造不等关系来确定参数的取值范围

例2 (同例1)

评析圆锥曲线中的范围问题类型较多，解法灵活多变，灵活选取不同的方法会为解题带来便利. 但总体上主要有两种方法：一是利用几何法，即通过利用曲线的定义、几何性质等进行求解；二是利用代数法，即把待求的几何量或代数表达式表示为某个参数的函数，然后利用函数方法、不等式方法等进行求解.与例1的解法(几何法)相比，本例的解法(代数法)就显得运算繁杂，对运算能力的要求较高，因此，圆锥曲线的解题中对方法的选择就显得尤为重要.

三、利用求函数值域方法将待求量表示为其它变量的函数，求其值域来确定参数的范围

例3 (2016·全国Ⅰ卷)设圆:

x2+y2+2x-15=0的圆心为A，直线l过点B(1，0)且与x轴不重合，l交圆A于C，D两点，过B作AC的平行线交AD于点E.

(1)证明|EA|+|EB|为定值，并写出点E的轨迹方程；

(2)设点E的轨迹为曲线C1，直线l交C1于M，N两点，过B且与l垂直的直线与圆A交于P，Q两点，求四边形MPNQ面积的取值范围.

分析(1)由椭圆的定义易得点E的轨迹方程.(2)解决直线与椭圆相关的问题，常规思路是先把直线方程与椭圆方程联立，消元、化简，然后应用根与系数的关系建立方程来解决相关的问题.本题中设出直线方程代入椭圆方程中，利用弦长公式求出|MN|，再利用点到直线的距离公式求出|PQ|，从而将四边形面积问题转化为关于k的函数问题，便可求得四边形面积的范围.

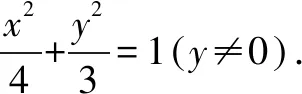
(2)当l与x轴不垂直时，

设l的方程为

y=k(x-1)(k≠0)，M(x1,y1)，N(x2,y2)，

将l方程代入椭圆得：

(4k2+3)x2-8k2x+4k2-12=0，

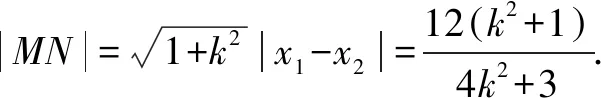
设过B且与l垂直的直线m为：

因此，所求四边形MPNQ的面积为

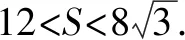
当l与x轴垂直时，易得四边形MPNQ的面积为12.

评析求四边形MPNQ面积的取值范围，我们可构造面积关于直线l的斜率的函数关系，通过S关于k的函数求得面积的范围，这是求解这类问题常用的方法.

四、利用已知参数的范围，求新参数的范围

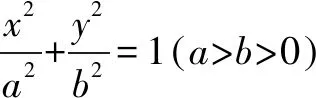
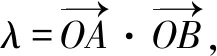
(1)求椭圆的方程；

(2)求k的取值范围；

(3)求△OAB的面积S的取值范围.

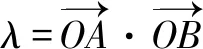
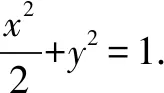
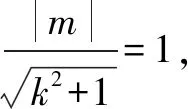
将l方程代入椭圆方程， 得：

(1+2k2)x2+4kmx+2m2-2=0.

设A(x1,y1)，B(x2,y2)，则

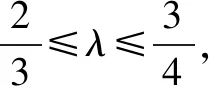
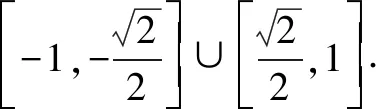
(3)由(1)(2)知，

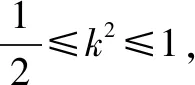
设△OAB的AB边上的高为d，则

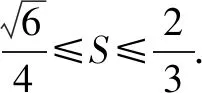
评析这种类型的问题是圆锥曲线中常见的问题.由已知参数的范围求新参数的范围思路相对简单，思维要求也不是很高，但对运算能力的要求比较高，必须引起对运算的高度重视，以便在高考中立于不败之地.

五、利用已知的不等关系构造不等式来确定参数的范围

例5 (2016·天津卷)设椭圆

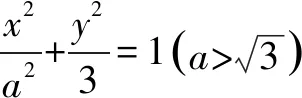
(1)求椭圆的方程；

(2)设过点A的直线l与椭圆交于点B(B不在x轴上)，垂直于l的直线与l交于点M，与y轴交于点H.若BF⊥HF，且∠MOA≤∠MAO，求直线l的斜率的取值范围.

分析(1)易得椭圆的标准方程；

(2)由角的不等关系化为边或坐标的不等关系，通过垂直关系简化为l的斜率与边或坐标的关系，解不等式便可得到所求范围.

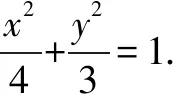
(2)设直线l的斜率为k(k≠0)，则直线l的方程为y=k(x-2).设B(xB,yB)， 将l的方程代入椭圆方程，得

(4k2+3)x2-16k2x+16k2-12=0.

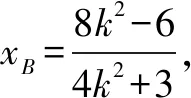
由(1)知F(1,0)，设H(0,yH)，所以，

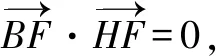
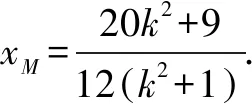
在△MAO，由∠MOA≤∠MAO得:

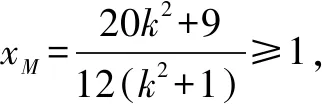
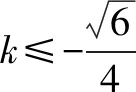
评析本题由角的不等关系来寻找边或坐标的不等关系是不太常见的题型.因此，圆锥曲线的学习除了关注运算能力外，对思维的灵活性、应变能力也是不容忽视的.

六、利用隐含的不等关系建立不等式来确定参数的范围

(1)当t=4，|AM|=|AN|时，求△AMN的面积；

(2)当2|AM|=|AN|时，求k的范围.

分析(1)易解△AMN的面积；

(2)根据点A的坐标写出AM的方程，与椭圆联立可求得|AM|；再用同样的方法或整体代换斜率k得到|AN|，利用2|AM|=|AN|得到k与t的关系式，依据隐含的t>3的范围可求得k的范围.

解法略.

评析直线与圆锥曲线的位置关系、弦长的计算方法等考查推理论证能力、运算能力以及转化化归等数学思想方法，能力要求高，难度大，是大家在复习学习中需要特别关注的问题.

圆锥曲线的解题策略主要体现在方法的选择和运算的机智应变上，只要我们在平时的学习中注意识别模式，择优定法，紧扣条件，布列方程，抓住主元，整体代换，围绕目标，化繁为简，经历这样的思考、分析，高考中的圆锥曲线问题便不在话下.