基于虚拟样机的片式凸轮箱性能改善研究
毛璐瑶,张华伟,刘 辉,张 帆
(1.广东省智能制造研究所,广东 广州 510070;2.广东硕泰智能装备有限公司,广东 中山 528403)
1 引言
接线端子是用于实现电气连接的一种配件产品,工业上划分为连接器的范畴,被广泛应用于工业及日常生活中,如3C、汽车连接端子、USB 连接线等等。一般接线端子内设置有导电插针,为实现高速稳定的将导电插针准确插入端子中,插针设备成为必不可少的设备[1]。凸轮插针机是一种复杂精密的工业生产设备[2],其只有一个电动机提供动力,通过电机带动主轴旋转,而主轴上的凸轮则可将装在插针模具上的针头上下移动进行插针,具有易组装、易维修、易操作、效率高、全自动化等优点,所以插针机对于电子行业来说是非常实用的生产设备[3]。凸轮箱为凸轮插针机的主要组成部分,其性能的好坏直接影响凸轮插针机的性能。片式凸轮箱国际上能做到500r/min[4],共轭凸轮箱最高能达到2000r/min。某国产片式凸轮箱,能在150r/min 时稳定工作,但以300r/min 以上速度运转时,会出现较大振动,出现夹针夹不到、夹不紧甚至卡死的情况。针利用试验测试及虚拟样机技术对该片式凸轮箱进行研究,分析限制该片式凸轮箱高速运转的原因,并寻求改进方案,使该产品能稳定的以600r/min 的速度工作,从而提高产品的工作效率和市场竞争力。
2 片式凸轮箱模型及材料参数
片式凸轮箱主要结构,如图1 所示。其主要零部件的材料为Q235-A,其材料参数,如表1 所示。

图1 片式凸轮箱三维模型Fig.1 3D Model of the Chip Cam Box
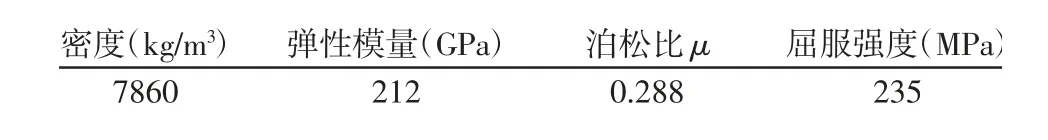
表1 材料参数Tab.1 Material Parameters
3 片式凸轮箱振动测试
片式凸轮箱在高速运转时,其振动幅度很大,因此有必要验证是否是由其结构共振导致。测试仪器有DEWEsoft 数据采集仪、加速度传感器、力锤,测试结果用Matlab 进行傅里叶变化,获得频响曲线。测点分别位于顶板、前板、左侧板、右侧板、左右连杆位置,凸轮箱振动测试系统,如图2 所示。

图2 凸轮箱振动测试Fig.2 Cam Box Vibration Test
将振动测试的时域结果进行傅里叶变换,进行频域分析[5]。(0~2000)Hz 范围内的频响曲线,如图3 所示。凸轮箱振动测试各测点(0~2000)Hz 范围内的频响曲线峰值所对应的频率,如表2所示。从振动测试结果来看,片式凸轮箱峰值频率较高,频率最低为29Hz,可能为凸轮箱某个细小零部件的振动频率,但最低频率远高于600r/min 时的10Hz,因此高速运转不会引起片式凸轮箱结构共振,结构共振并非是限制其高速运转的因素。

图3 各测点频响曲线Fig.3 Frequency Response Curve of Each Measuring Point

表2 频响曲线峰值对应的频率Tab.2 Frequency Corresponding to the Peak Value of the Frequency Response Curve
4 片式凸轮箱运动学模型的建立
虚拟样机技术是CAE 的一个重要分支,是在人们开发新的产品时,在概念设计阶段,通过学科理论和计算机语言,对设计阶段的产品进行虚拟性能测试,达到提升设计性能,降低设计成本,减少产品开发时间的目的[6]。ADAMS 是一款以多体动力学为基础的运动学分析软件,其可建立复杂机械系统的运动学和动力学模型[7]。
首先在几何处理软件(如Spcaeclaim)中对片式凸轮箱3 维模型进行简化。然后导入ADAMS 建立凸轮箱的虚拟样机,设置各部件材料及各个零部件之间的运动副、弹簧和接触,片式凸轮箱弹簧位置,如图3 所示。弹簧刚度系数K和阻尼系数C,如表3所示。在建立片式凸轮箱运动学模型时,各弹簧的阻尼系数取0.03N·s/m,此时并未考虑各部件间因摩擦阻尼等因素所带来的阻尼效果。在凸轮轴的旋转副上施加旋转驱动。
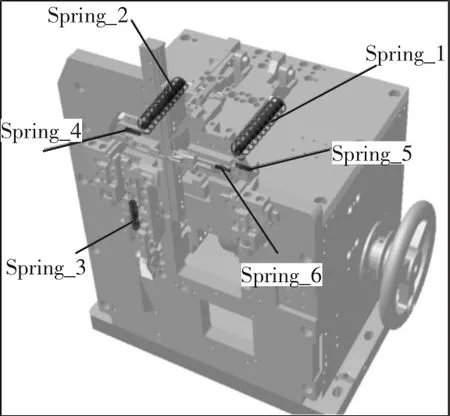
图4 凸轮箱运动学模型Fig.4 Cam Box Kinematics Model

图5 60r/min 时标记点的运动轨迹Fig.5 Motion Track of Marker Points at 60r/Min

表3 凸轮箱各弹簧初始参数Tab.3 Initial Parameters of Each Spring of the Cam Box
对于n自由度有阻尼强迫振动,其数学表达式为:

式中:M—质量矩阵;C—阻尼矩阵;K—刚度矩阵。
为了简化,考虑阻尼矩阵可视为质量矩阵和刚度矩阵的线性组合,即:

式中:X—无阻尼系统固有振型;
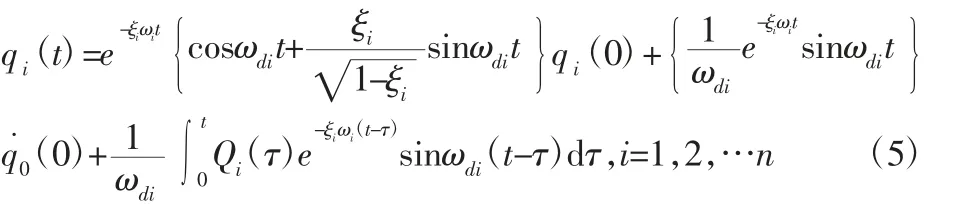
式中:ξi—对应于第i阶固有振型的模态阻尼比;

式中:ωi—无阻尼系统第i阶固有频率;
由于对于无阻尼系统有:

因此有阻尼的多自由度受迫振动,其各自由度质点的位移矩阵x与质量矩阵M、刚度矩阵K、阻尼矩阵C和载荷矩阵F(t)有关。系统的刚度K变大时,系统的固有频率ω 变大。该片式凸轮箱,左切刀有3 个弹簧,可视为3 自由度有阻尼受迫振动系统;右切刀有2 个弹簧,可视为单自由度有阻尼受迫振动系统。当其结构形式及弹簧驱动方式不变(不增加阻尼器)时,其结构的质量矩阵M和阻尼矩阵C基本保持不变,左右切刀的运动主要受到各弹簧刚度K的影响[8-9]。
5 不同转速凸轮箱运动情况
5.1 60r/min 时片式凸轮箱运动情况
给凸轮轴施加一个-360d*time 的旋转驱动,设置参考点,反映所关心位置的运动情况:在左切刀与右切刀接触面上各设置一个标记点Marker_BJ1 和MARKER_BJ2。计算10s,10 个周期,1000 个载荷步,研究低速情况下左右切刀的运动情况。仿真完后运行动画,显示两个标记点的运行轨迹,如图5 所示。在60r/min的低速状态下,其运行平稳,在一个周期的特定时间内,Marker_BJ1 和BJ2 的运行轨迹保持平行。
60r/min 时,左右切刀接触力随时间的变化曲线,如图6 所示。从曲线图可以看出接触力是周期性出现的。在每个周期的特定时间段内,左右切刀之间发生接触,存在接触力(但每个周期的接触力不一定相等)。由于在每个接触的时间段内,有某些时间点的接触力为零,因此在计算时不能以接触力是否为0 判定左右切刀能否正常夹持工件。因为该仿真中并未考虑被夹持的工件,而工件有一定的尺寸,即便左右切刀有微小的脱离(此时该计算接触力为零)仍能保持夹紧工件。记点MARKER_BJ1 和MARKER_BJ2 在X方向(水平方向)的相对位移曲线DX_BJ1_BJ2,如图7 所示。从DX_BJ1_BJ2 的相对位移曲线可以看出,每个周期的(0.11~0.47)T 之间位移最小,为其夹针阶段,左右切刀保持接触。因此要保证其正常工作,在每个周期的(0.11~0.47)T 这个区段

图6 60r/min 时左右切刀接触力曲线Fig.6 Contact Force Curve of the Left and Right Cutters at 60r/min
DX_BJ1_BJ2 应小于某个值。图7 60r/min 时BJ1 和BJ2 水平方向的距离曲线
Fig.7 Displacement Curve of BJ1 and BJ2 in Horizontal Direction at 60r/min
取Const_DX 曲线作为判断左右切刀是否能夹紧针的依据,其取值为:

式中:time—运行时间;mod(time,T)—time 整除T后的余数。
当Const_DX 大于0.25mm 时,可判定为出现夹不紧夹不到针的情况。在ADAMS 中用IF 函数实现Const_DX:Const_DX=if(mod(time,T)-0.47*T:if(mod(time,T)-0.11*T:0.1,0.1,DX_BJ1_BJ2*1),0.1,0.1)。
60r/min 时Const_DX 曲线,如图8 所示。

图8 60r/min 时Const_DX 曲线Fig.8 Const_DX Curve at 60r/min
5.2 片式凸轮箱不同转速运动情况分析
片式凸轮箱不同转速下10 个周期标记点的运动轨迹,如图9 所示。随着转速的提高,左右切刀抖动的厉害,右切刀尤为明显。从两个标记点BJ1 和BJ2 的运行轨迹上看,在接触区间段其轨迹曲线:60r/min 时,左切刀BJ1 和右切刀BJ2 运行轨迹基本为直线,且几乎平行;150r/min,左切刀BJ1 为直线,右切刀BJ2 轨迹出现小幅度抖动;300r/min 时,左切刀BJ1 近似直线,右切刀BJ2出现较大抖动;600r/min 时,左切刀BJ1 近似直线,右切刀BJ2 出现很大抖动。高速运转时,右切刀相对左切刀的振动幅度更大,右切刀相比左切刀多了一个Spring_6,说明弹簧对片式凸轮箱的高速运转有较大的影响。

图9 不同转速时的运动轨迹Fig.9 Motion Trajectories at Different Speeds
150r/min、300r/min、600r/min 转速下的Const_DX 曲线图,如图10 所示。在150r/min 时,Const_DX 能够保持在较低的水平,能够正常工作。但是在达到300r/min 时就会出现Const_DX 较大的情况,此时会出现夹不住针的情况。当转速达到600r/min 时,Const_DX 会出现很大值的情况,此时凸轮箱在1s 内的10 个周期中会出现几个周期夹不到和夹不住针的情况。
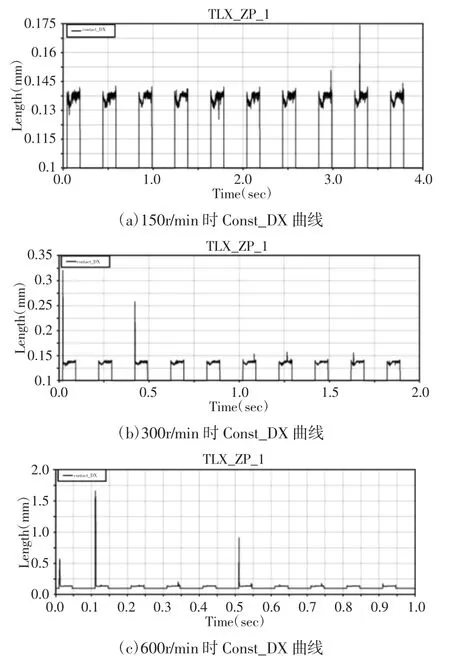
图10 不同转速时的Const_DX 曲线Fig.10 Const_DX Curves of Different Speeds
6 片式凸轮箱参数优化
根据前文分析,弹簧对片式凸轮箱高速运转影响较大。由于左右切刀夹针时为水平运动,左切刀受到Spring_4 的影响,而右切刀主要受到Spring_5 和Spring_6 的影响。因此对Spring_4、Spring_5、Spring_6 重新选型,以满足600r/min 转速的要求。Spring_1、Spring_2、Spring_3 的弹簧型号不变,Spring_4 和Spring_5 采用相同型号,以Spring_4 、Spring_5、Spring_6 的弹簧刚度K_45 和K_6 作为设计变量,Const_DX 最大值作为目标函数进行试验研究,要求Con_DX 最大值小于0.25mm。满足Spring_4、Spring_5、Spring_6 的弹簧刚度取值,如表4 所示。总共进行36 次试验。

表4 K45 和K_6 的取值Tab.4 The Value of K_45 and K_6
每次试验对应的Const_DX 最大值曲线,如图11 所示。随着弹簧组合的变化,共有4 个组合使Const_DX 最大值较小,分别是第3、17、23、29 次试验,这四次试验对应的Const_DX 最大值和弹簧刚度,如表5 所示。从图11 和表5 可以看出,K_45 和K_6 并非越大越好,也不是越小越好,而是有一个合理的搭配。这是因为,在(0.11~0.47)T 的区间范围内,左右切刀均要同步到达夹针位置,因此需要K_45 和K_6 尽量大,以保证左右切刀在接触后回弹的足够快,以便能夹到针。但是弹簧刚度的增大又会导致左右切刀在夹针时的接触力变大,使得左右切刀在夹针阶段受到接触力作用时振动的幅度变大,振荡衰减需要的时间变长,从而导致夹不到针,或者夹针松弛的情况发生,即Const_DX 最大值超出限定要求。因此K_45 和K_6 有一个最优的组合。

图11 每次试验研究对应的Const_DX 最大值曲线Fig.11 Const_DX Maximum Curve for Each Experimental Study

表5 满足条件的试验Tab.5 Tests that Meet the Conditions
转速为600r/min 时Trial17 的弹簧刚度取值最优,其轨迹曲线,如图12 所示。对比图9 可以看出,采用Trial17 弹簧参数的凸轮箱在600r/min 时的运动情况较优化前有明显改善。优化前后的Const_DX曲线,如图13 所示。从图13 中可以看出采用Trial17 弹簧参数的Const_DX 曲线最大值在0.135mm,而初始参数下的Const_DX最大值达到1.6619mm。优化后的Const_DX 曲线每个周期接触阶段的值低于优于优化前的,说明采用新的弹簧型号的片式凸轮箱高速性能大大改观,能满足在特定时间段夹紧针的设计要求。

图12 Trial 17 600r/min 时标记点BJ1 和BJ2 轨迹曲线Fig.12 Trace Point BJ1 and BJ2 Trajectory Curves at Trial 17 600r/min

图13 初始参数与采用Trial_17 弹簧的Const_DX 曲线对比(局部放大)Fig.13 Comparison of Initial Parameters with the Const_DX Curve Using the Trial_17 Spring(Partial Enlargement)
7 结论
通过对片式凸轮箱进行振动测试及运动学仿真,分析出片式凸轮箱高速运行时出现振动大,夹针夹不到夹不紧的主要因素不是结构的共振,而是凸轮箱弹簧的选型不合理。通过虚拟样机技术对凸轮箱进行运动学仿真,获得其在不同转速下左右切刀的运动轨迹,从而得到一个衡量其是否能满足夹针要求的判定标准。由于左右切刀受到弹簧Spring_4、Spring_5 和Spring_6 的影响,弹簧刚度过大将导致接触力的变大,在夹针阶段振动衰减的时间变长;弹簧刚度过小,将导致其在夹针阶段左右切刀不能及时回弹,因此利用ADAMS 的试验研究获得了一组能够使凸轮箱满足600r/min 转速下稳定运行的最优参数,从而为片式凸轮箱性能的改善提供了依据。

