车辆稳定换道时的侧向加速度分析
王树凤,孙文盛,刘宗锋
(山东科技大学交通学院,山东 青岛 266590)
1 引言
随着汽车保有量的增加,交通事故已成为人类死亡的主要原因之一,汽车主动安全技术是减少交通事故的重要措施,目前研究已逐渐从纵向稳定性控制向纵横向稳定性控制领域拓展。文献[1]提出利用主动防侧倾杆和电子稳定控制器(ESP)降低车速和侧向加速度,提高汽车的横向稳定性。文献[2]对换道侧向加速度的取值进行了具体的量化,车辆紧急转向变道时,认为其在限制级与最大级之间。文献[3]提出了四轮驱动(4WD)控制算法来提高车辆的操纵性和横向稳定性,防止汽车侧翻。文献[4]设计一种利用磁流变阻尼器使汽车悬架获得变刚度和阻尼能力的系统来提高汽车的横向稳定性。横向稳定性控制常用侧向加速度等指标来进行衡量,但是关于换道侧向加速度的研究较少,一般都采用常规取值代替。侧向加速度不仅和车辆本身的结构、行驶状态有关,而且和路面附着条件有关。
以车辆换道时的侧向加速度为研究对象,首先从车辆运动学角度,根据换道轨迹推导车辆侧向加速度、速度与路面系数间关系,然后使用ADAMS/CAR 建立车辆虚拟样机模型进行换道仿真,从动力学角度获取不同路面下车速与侧向加速度间的关系,并与常规取值、理论分析进行比较。
2 换道侧向加速度的理论分析
2.1 换道侧向加速度的常规取值
换道是车辆行驶中常见的行为,为分析其换道过程中的操纵稳定性,可通过典型行驶工况中的单移线试验来进行分析,参考双移线试验的标准设定如下[5]。在汽车换道过程中,为了保证汽车横向稳定性,要求车辆转向时车体的侧向加速度不超过0.4g[6],该数据是在附着系数良好的公路上,车辆处于线性条件下工作时得到的结论。但在实际行驶过程中,车辆侧向加速度不仅受车辆本身状态的影响,还和车速、道路状况等密切相关。单移线试验,如图1所示。
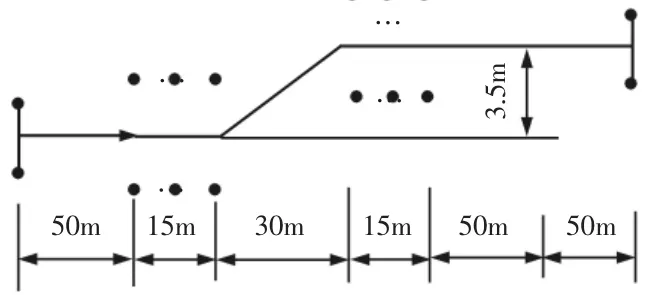
图1 单移线试验Fig.1 Single-Lane Change Maneuver Test
2.2 运动学理论分析
从运动学角度进行分析,根据换道轨迹、速度等运动学参数分析其侧向加速度。相关学者对换道轨迹已做了大量研究,大多从横向位移函数着手,利用圆弧曲线[7]、贝塞尔样条曲线[8]或高次多项式[9]拟合轨迹。基于变道轨迹所满足的诸多准则,并对近几年的各种变道轨迹模型进行对比发现,五次多项式轨迹函数不仅具有三阶连续可导和曲率连续不突变的优点,还能很好地模拟实际换道轨迹,符合驾驶员实际驾驶习惯。故采用五次多项式拟合的变道轨迹函数,其表达式为:

式中:x—车辆在参考路径上沿行驶方向的坐标;y—车辆在参考
路径上的侧向坐标;ci—五次多项式的系数。
假设车辆的位置在换道起点为(x1,y1),结束时为(x2,y2)。完成换道时车辆横向偏移量ye=y2-y1,纵向行驶距离xe=x2-x1,系数可通过边界初始及终止约束[10-11]确定,如表1 所示。

表1 换道路径需满足的准则Tab.1 The Criteria of Lane Changing
表中:κ—曲线y(x)的曲率。
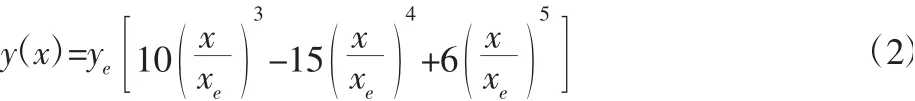
由此可求出五次多项式系数ci,公式如下:式中:ye—完成整个变道过程的侧向位移;xe—完成整个变道过程
的纵向位移。
由于换道时间短,可将纵向速度u设为定值,整个换道时间为te,对式(2)整理可得:

对上式求二阶导得换道时侧向加速度与时间的关系如下:

由文献[12]可知,车辆换道时持续时间的一般在(1~6.8)s 之间,文中以2.5s 为例,使用MATLAB 分别绘制了换道轨迹、侧向加速度的变化曲线,如图2 所示。
从图2 可以看出,侧向加速度在[0,te]内存在最大值和最小值。对ay(t)求导并令其导数为0,解方程得到极值点,获得侧向加速度极大值:


图2 侧向位移、侧向加速度曲线Fig.2 Curves of Lateral Displacement and Lateral Acceleration
车辆的侧向加速度与侧向力有关。车辆在行驶时受到来自地面的纵向作用力以及侧向用力,二者的合力取决于轮胎与地面的附着力,且侧向力与纵向力还应符合摩擦椭圆的约束,即:

式中:μ—路面附着系数;
Fx—轮胎与路面的纵向作用力;
Fy—轮胎与路面的侧向作用力;
Fxmax—轮胎所能提供的最大纵向作用力;
Fymax—轮胎所能提供的最大侧向作用力。
由以上分析可知,确定车速、车道宽度后,得到最大侧向加速度与时间的变化关系曲线,按标准试验确定换道纵向距离,取换道前后10m 和中间30m 作为换道过程中的纵向位移,即可获得侧向加速度与速度的变化关系曲线,如图3 所示。

图3 最大侧向加速度与速度的关系曲线Fig.3 The Relation of Lateral Acceleration and Velocity
3 基于ADAMS/Car 整车换道仿真分析
以上理论分析只是单纯考虑换道轨迹,但是在实际车辆转弯换道时,车辆动力学特性非常重要,其决定了车辆能否安全稳定换道。因此以某一样车为例,利用ADAMS/Car 建立反应真实结构的车辆模型,对其进行换道的动力学仿真分析,获取车速与侧向加速度之间的关系。
3.1 理论分析
以某车辆为原型,建立包含车身、悬架、转向、轮胎等系统的整车模型,如图4 所示。主要参数,如表2 所示。
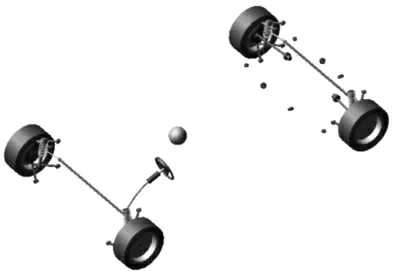
图4 整车虚拟样机模型Fig.4 Vehicle Virtual Prototype Model

表2 车辆参数Tab.2 Vehicle Parameters
3.2 仿真设置

图5 仿真流程图Fig.5 The Flow Chart of Simulation
典型行驶工况中的单移线试验,转向换道试验属于人-车-路闭环试验,ADAMS/Car 首先根据输入的仿真分析条件得到所需的控制信息、模型信息等,调用求解器进行运动学、动力学运算,根据反馈信息调用闭环算法满足仿真试验要求,最后将计算结果输出。单移线试验的轨迹已经给出。由于侧向加速度不仅和车辆、速度等因素有关,与路面附着条件也有关系,根据实际情况,速度区间取(30~120)km/h,取理想路面(附着系数1.0),一般路面(附着系数0.75)、湿滑路面(附着系数0.55)以及冰雪路面(附着系数0.15)四种不同路况分析。其中输入信息:(1)驱动控制文件(Driver Control File,*.dcf):驱动控制文件描述了车辆模型准备执行的一系列操作,该仿真中需要设定车辆行驶的速度、控制方式、对驱动参数文件(*.dcd)的调用以及试验结束的信息。(2)驱动参数文件(Driver Control Data File,*.dcd):该文件必须与驱动控制文件(*.dcf)配合使用,包含了驱动控制文件所需的换道轨迹线数据,该数据与理论分析中的五次多项式的换道轨迹对应。输出参数有:侧向加速度(g),侧向位移曲线(mm),纵向速度(km/h)。本仿真中车辆以不同速度、不同路面附着系数沿着同一换道轨迹进行换道,分析其侧向加速度的变化情况。其主要流程如下:(1)输入路面附着系数、车速;(2)换道仿真分析,判断失稳;(3)输出位移、速度、侧向加速度;(4)改变参数,重复以上步骤,如图5所示。
3.3 仿真结果分析
3.3.1 换道仿真分析
换道失稳一般发生在高速情况下,首先对正常道路(附着系数0.75)高速下的换道过程进行分析,车辆以120km/h 的速度行驶进行换道过程中车辆的侧向加速度、侧向位移以及纵向速度的仿真输出结果,如图6 所示。
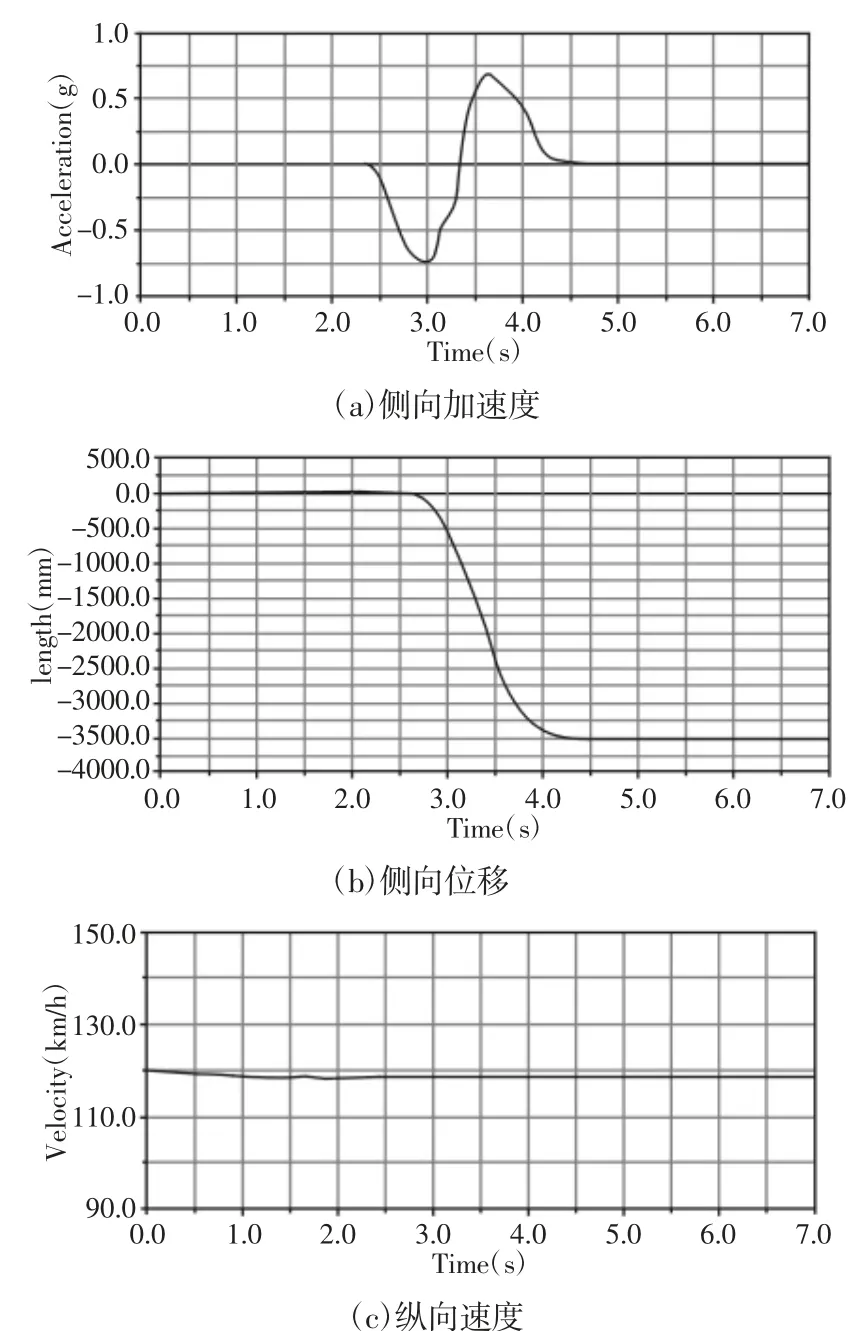
图6 车速120km/h 换道过程中输出参数的变化Fig.6 The Change of Output Parameters in the Process of 120km/h
从图6(a)可知,换道过程中侧向加速度曲线变化平稳,没出现急剧变化的情况,表明车辆安全稳定的换道。由图6(b)可知,车辆与预定的换道轨迹一致,较好实现了路径跟踪。从图6(c)可知,在转向过程中纵向速度变化不大,也说明了理论分析中假设紧急转向换道过程中车速不变的可行性。
120km/h 时三种方法对应的最大侧向加速度如下:(1)动力学仿真:从图6(a)可知,侧向加速度为0.52g;(2)运动学分析:从图3 可知,侧向加速度为0.75g;(3)常规值:0.4g。
从以上分析可知,运动学仿真最高,其没考虑车辆的动力学特性以及路面特性;动力学仿真相对来说,更贴合实际车辆;对于常规值0.4g,对于高速下的换道,其数值偏低。
3.3.2 不同工况下最大侧向加速度变化
分别对车速在(30~120)km/h 范围内换道时的最大侧向加速度进行统计分析,冰雪路面(μ=0.15)下超过30km/h 时换道失稳。统计数据,如表3 所示。对不同路面条件下的速度、加速度数据进行曲线拟合,如图7 所示。从图中可以看出:(1)最大侧向加速度随着车速的增长呈上升趋势,约成正比关系。(2)中低速时(60km/h),湿滑路面下最大侧向加速度基本与正常道路下的相同,但在高速时,随着速度的增大,二者之间的差距越来越大。附着系数越大,最大侧向加速度越大。

表3 不同附着系数下的最大侧向加速度Tab.3 Maximum Lateral Acceleration of Different Adhesion Coefficients

图7 不同路面条件下侧向加速度与速度的关系Fig.7 The Relationship Between Lateral Acceleration and Velocity Under Different Conditions
4 侧向加速度分析比较
为了更好的分析不同速度下的侧向加速度,将常规取值、运动学分析、动力学分析条件下车速与侧向加速度值的关系绘制一起,如图8 所示。由图8 中的数据进行对比,可知:
(1)侧向加速度随着速度的增加而增加,采用运动学分析与动力学分析两种方法得到的加速度数值差距越来越大。
高速时,车辆的动力学特性对侧向加速度影响很大,动力学分析的数据准确,但是建模复杂,而且车辆参数不同结果差别也较大,无法应用到车辆的主动安全控制中。
中低速时,运动学分析数值稍高,但是数值都小于常规取值;该工况对应城市道路较通畅情况下的换道,一般城市道路车速在(40~60)km/h 之间。
(2)当车速<114km/h 时侧向加速度达不到常规取值(采用动力学分析),当速度高于此值时,虽然超过常规值,但车辆还是处于稳定状态,说明常规取值是偏于安全的。
(3)综合考虑车辆安全及路面附着系数的影响,把附着系数引入到最大侧向加速度中,即按照正常道路的附着系数(附着系数0.75)计算,也即0.4g=0.533μg。该数值与表2 中的车速在100km/h 附近不同附着系数的计算结果基本对应,此时最大侧向加速度为0.533μg 是偏于安全的。
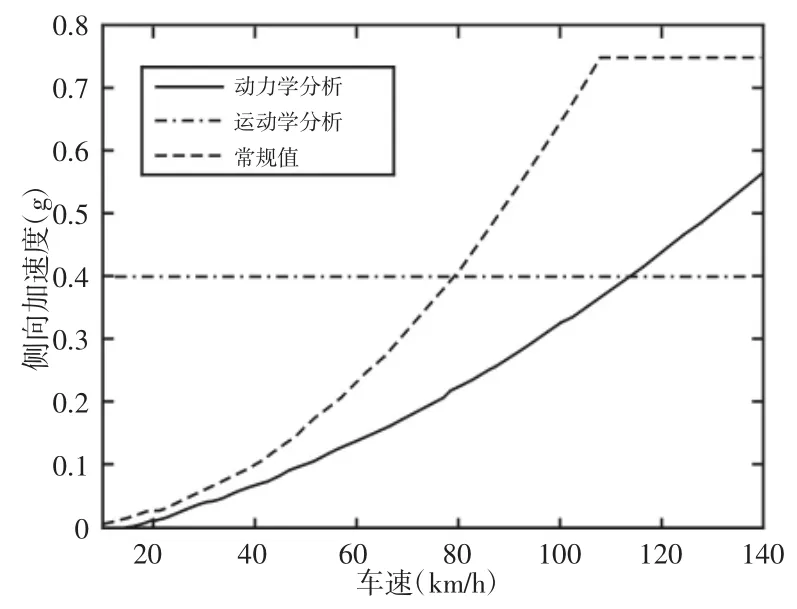
图8 三种不同的角度下侧向加速度与速度的关系图Fig.8 The Relationship Between the Lateral Acceleration and the Velocity in Three Different Cases
5 结论
以换道时的最大侧向加速度为研究对象,分别从运动学和动力学角度,分析在换道轨迹确定下,换道行驶过程中侧向加速度与车速、道路附着系数之间的关系。考虑车辆换道的安全稳定性,综合常规取值进行对比,结论如下:(1)侧向加速度最大值随车速的增大而增大,随着附着系数的减小而减小。中低速行驶时,正常道路和湿滑道路相差不大,但是在冰雪路面上,车辆容易失稳;(2)动力学分析结果较精确,但其建模与仿真复杂,不适应车辆的实时控制;运动学分析可用公式对不同车辆、不同工况进行统一表示,适合应用到实时控制中,但其较少考虑车辆的动力学特性,需把附着系数、车速等约束融入到公式中;(3)对常规取值0.4g 进行了改进,把附着系数引入到最大侧向加速度中,修改为0.533μg。研究可为车辆换道时提供参考,为智能车辆自动换道的研究提供理论依据。

