面向装配序列规划的最小生成树方法

冯立艳，何世伟，耿 浩，关铁成

（华北理工大学机械工程学院，河北 唐山 063210）

1 引言

装配序列是将装配件表示为一定约束条件下的零件序列[1]。对于包含零件多、要求精度高、结构复杂、装配空间狭小的产品，装配产生的费用将会达到产品制造成本的（30～50）%。若一个装配体由N个零件组成，每个零件至少有m种可能的装配方法，则可能的装配序列为mNN！种。因此规划最优装配序列具有重要意义，它可以明显改善装配速度，提高装配质量，降低成本[2-4]。

国内很多学者对装配序列的产生方法进行研究，文献[5]通过对有向装配连接图的割集分解计算，实现了装配序列生成；文献[6]建立了基于符号有序二叉决策图模型及操作的可行装配序列生成技术；文献[7]设计了一个基于自动拆卸过程的装配序列生成算法。通过建立装配体的零件连接图，对连接零件之间的密切程度进行量化计算并赋予它们之间的边，再通过运筹学中求解最小生成树的破圈法对零件连接图的边进行破除，最后得到最优的装配序列。

连通且不含环的无向图称为树。最小生成树在数学上定义为连接所有节点的子网，所有连接权重之和最小，不存在循环。破圈法是一种简单直观的寻找最小生成树的算法。

2 装配关系密切程度的量化指标

装配模型是装配序列规划的基础，所依据的装配模型是零件连接图，用顶点表示零件，用连接顶点之间的边表示零件之间的连接关系。装配体中的一个零件可与多个零件存在装配关系，影响两零件间装配关系密切程度的因素有很多，可归纳为以下3个可量化的指标[8-10]。

2.1 稳定支撑指标

装配后有直接接触的两个零件i、j，当零件i的重力方向垂直且穿过两零件的接触面时，称j对i有稳定支撑作用。若两零件互相有稳定支撑作用，则记两零件间稳定支撑指标值bij=2；若只有一个零件对另一零件有稳定支撑作用，记bij=1；否则记bij=0。

设一装配体中任意两零件间最大的稳定支撑指标值为bmax，则归一化后的稳定支撑指标值为：

2.2 约束自由度指标

零件的装配方向为六个平动方向，约束自由度指标cij指两零件互为固定件时，另一个零件装配后减少的平动自由度的和。

式中：cij—以零件i为固定件时，零件j减少的平动自由度；cji—以零件j为固定件时，零件i减少的平动自由度。

设一装配体中任意两零件间最大的约束自由度指标值为cmax，则归一化后的约束自由度指标值Cij为：

2.3 连接强度指标

两零件连接的越稳固，那么它们在装配后作为一个整体参与后续装配时抵抗装配关系被破坏的能力就越强。

在侦查成本与侦查效益的运行关系中，如果侦查决策正确、恰当，那么侦查成本与侦查效益将会呈现出一种同向运行状态;而如果侦查决策不恰当，那么侦查成本与侦查效益将会出现一种异向运行状态。

零件i和j之间装配关系的归一化后连接强度指标值为Dij，若两零件只是表面接触，则记Dij=0。参照LEE 建立的常见联接类型的联接强度指标[8]，以焊接为最稳固连接，建立其他装配类型的连接强度归一化后的指标值，如表1 所示。

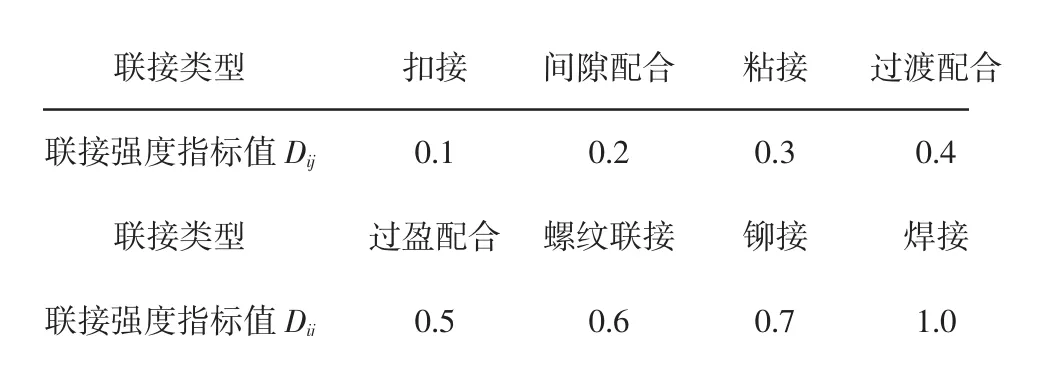
表1 连接强度指标值Tab.1 Connection Strength Index Value

综合上述三个量化指标，用λij表示装配关系密切值，代表零件i与零件j之间装配关系的密切相关程度，评分值越高，表示越推荐这两个零件进行直接装配，有：

式中：ωB、ωC、ωD—稳定支撑指标、约束自由度指标和连接强度指标所占比重，因此有：

3 装配关系干涉的表达

在零件连接图中，零件i与零件j之间的连线代表两零件装配关系，记作eij。若装配关系eij先于其他装配关系完成时，会影响其他n个装配关系，则称该装配干涉值为n，记为eij=n。

以图1（a）的子弹解剖图为例，说明零件连接图及装配干涉eij的取值。其零件连接图如图1（b）所示。图1（a）中，在弹头与弹壳装配后，就无法再装入火药，即装配关系e13干涉了装配关系e23；而若弹壳在与底火装配之前装入火药，虽然不会使底火无法装配，但大大增加了底火的装配难度，即装配关系e23干涉了装配关系e34；装配关系e34不会干涉e13和e23。因为e13和e23都干涉了1 个装配关系，而e34没有干涉任何装配关系，则e13=1、e23=1、e34=0。标注干涉值后的子弹零件连接图，如图1（c）所示。

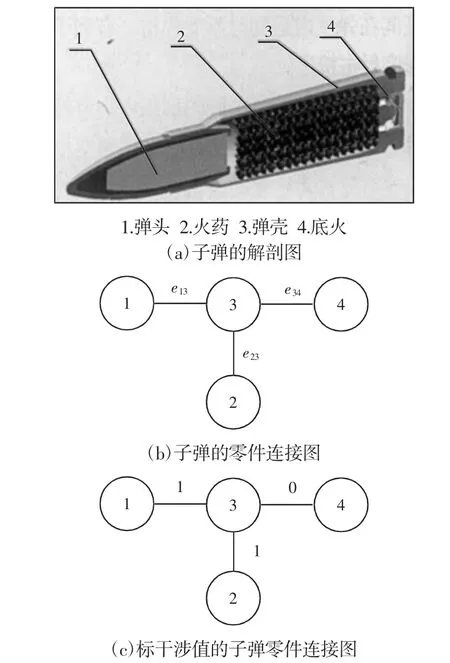
图1 子弹解剖图及其装配体生成树Fig.1 Bullet Section View and Its Assembly Spanning Tree

4 基于破圈法的装配序列求解方法

获得装配序列的流程图，如图2 所示。对其主要内容解释如下。

4.1 破圈

用破圈法寻找最小生成树的步骤如下：

（1）先任取一个圈，从圈中去掉一条权重最大的边。若在同一圈中有2 条或2 条以上权重最大边，则任选其中之一去掉。

（2）在余下的子圈中，重复上述步骤，直至没有圈为止。

所有破圈完成后，则由零件连接图得到最大密切程度的装配体生成树。

4.2 装配序列的生成

分析树中每个装配关系的干涉值，并标在对应边上，则可根据标注有干涉值的装配体生成树产生装配序列，步骤如下：

（1）任选标号为0 的两零件开始装配。

（2）每装配一步，将装配好的两零件（或子装配体）视为一个零件，再对余下的装配关系重新进行干涉值分析并赋值。

重复以上步骤，同时按顺序记录已装配零件的序号，直到所有零件装配完毕，记录好的零件顺序即为最优装配序列（根据装配方向集中原则，进行一步装配之后，若条件允许，应优先选择同一条树枝上的零件继续装配）。

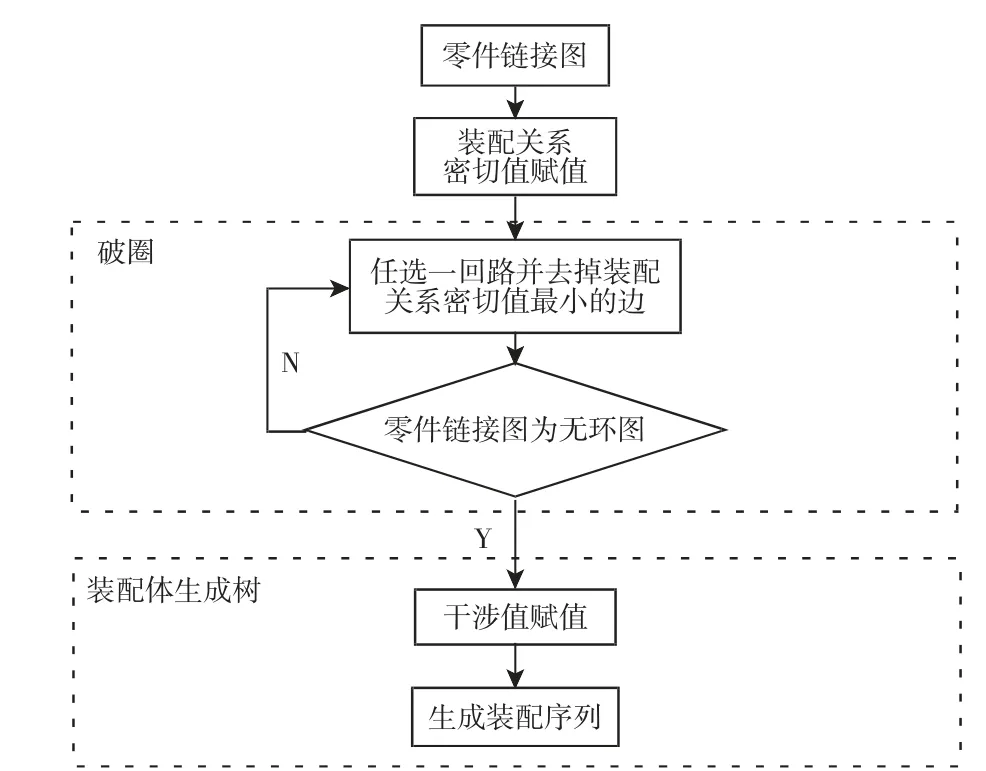
图2 装配序列获取流程图Fig.2 Assembly Sequence Acquisition Flow Chart

5 实例分析

以汽油机驱动的水泵作为实例，如图3 所示。说明提出的装配序列生成方法。

水泵由15 个零件组成，通过汽油机的曲轴5 转动，带动泵叶片10 转动，将由进水嘴14 进入的水通过排水嘴2 喷出。其中阀1 与排水嘴2、泵塞15 与泵箱4、曲轴5 与泵叶片10、泵盖6与泵箱4、排水嘴2 与泵箱4、进水嘴14 与泵箱4 均为螺纹联接；密封圈B（8）与弹簧9 为间隙配合；泵箱4 与轮盖垫圈12、泵箱4与胶皮垫13、密封圈A（7）与密封圈B（8）、弹簧9 与泵叶片10 仅有表面接触；其余邻接零件的装配均为过盈连接。

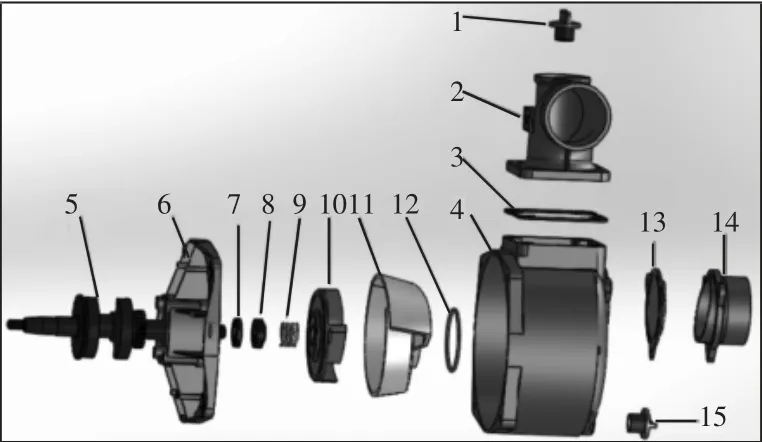
图3 汽油机驱动的水泵装配分解图Fig.3 Assembly Decomposition Diagram of Water Pump Driven by Gasoline Engine

第一步：建立水泵的零件连接图，如图4（a）所示。并对环中所有边进行装配关系密切值计算，处于封闭环中的边有4-11，4-12，4-13，4-14，5-7，5-8，5-9，5-10，6-7，6-8，7-8，8-9，9-10，11-12，13-14。取ωB，ωC，ωD分别为0.3、0.3、0.4，装配关系密切值的计算过程，如表2 所示。将计算所得λij赋给对应的边，如图4（b）所示。

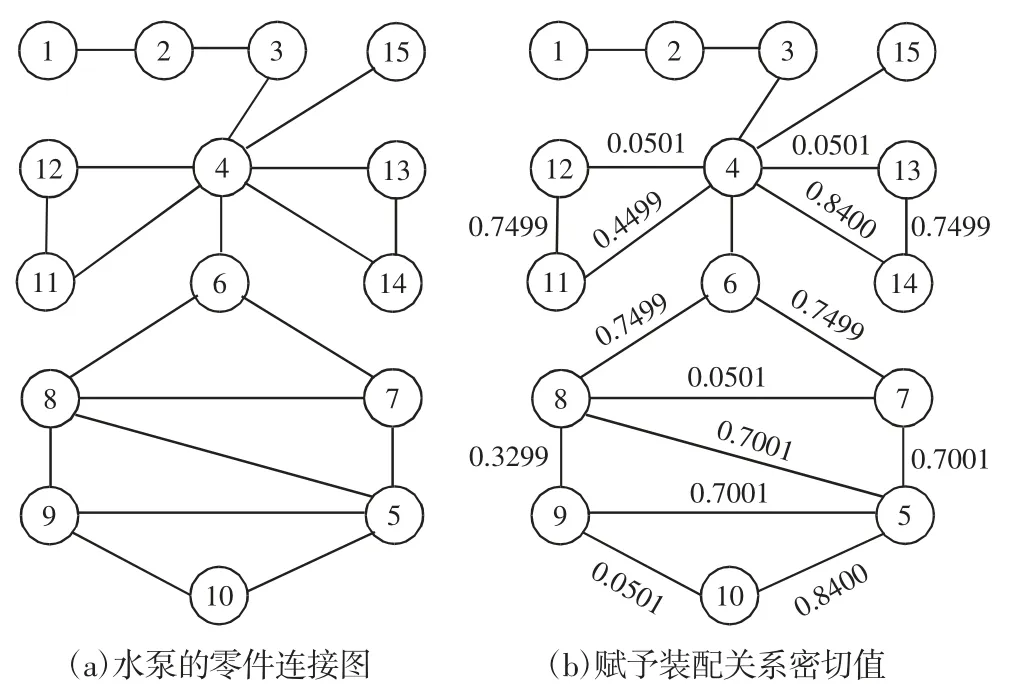
图4 水泵零件连接图与装配关系密切值赋值Fig.4 Connection Diagram of Pump Parts and Osculation-Value

第二步：对零件连接图破圈。如在封闭环6-7-8 中，7 与8 之间的装配关系密切值最小，则去掉7 与8 之间的边，这样，6-7-5-8 则形成一个封闭环，其中5-7、5-8 同时为装配关系密切值最小的边，则任选一条去掉即可，如去掉5-8。在余下的子圈中，重复上述工作，直至没有圈为止，得到装配体生成树，如图5（a）所示。

第三步：干涉分析。若将泵箱4 和泵盖6 先装配起来，则会导致7、8、9、10、11、12 这6 个零件无法装配，故e46=6；若将曲轴5与泵叶片10 先进行装配，则会导致6、7、8、9 这4 个零件无法装配，故e510=4。将所有干涉值赋予对应的边，如图5（b）所示。第四步：生成序列。水泵的装配过程，如图6 所示。在图5（b）中，选择干涉值为0 的装配关系先进行装配。先把1，2，3，4，15 五个零件装配在一起，并将其视为一个部件参与以后的装配，如图6（a）所示；图6（b）中，11-12，13-14 装配后，将11 与12，13 与14视为一个部件再与部件1-2-3-4-15 装配时，原本的干涉就不存在了，故对应的干涉值由1 改为0。以此类推，余下的装配过程，如图6（c）～图6（g）所示。

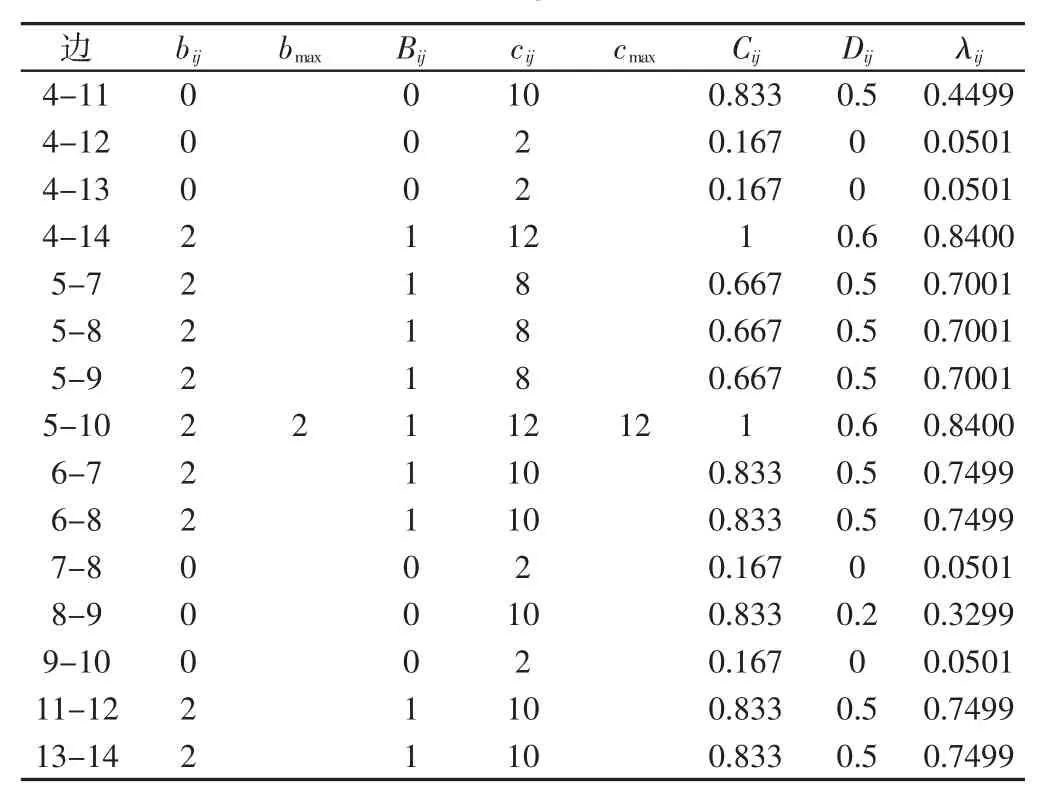
表2 装配关系密切值的计算Tab.2 Calculation of Assembly Relation Osculation-Value

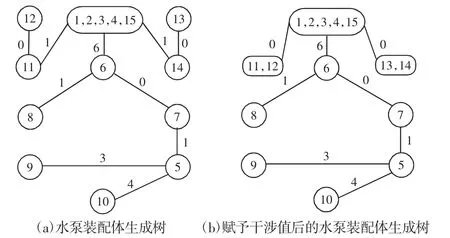
图5 水泵装配体生成树及干涉分析Fig.5 Assembly Spanning Tree and Interference Analysis

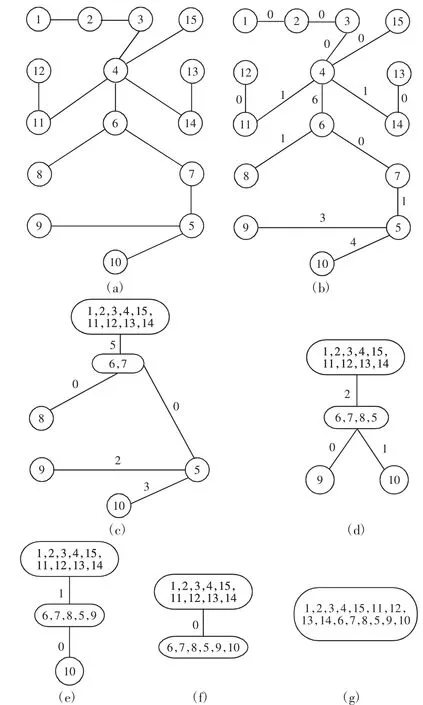
图6 水泵装配序列生成过程Fig.6 Sequence Generation of Pump Assembly

6 结论

（1）将最小生成树问题与装配序列规划有机结合起来，提出了一种装配序列规划的新方法。（2）分析了影响零件间装配关系密切程度的主要因素，建立了装配关系密切值的定量计算方法。该方法为后续工作，如装配序列评价提供了便利。（3）运用破圈法剔除了大量无效序列，一定程度上简化了装配序列规划的求解，装配体零件数量越大，简化程度越明显。（4）最优序列伴随干涉分析的进行而自动生成，生成的序列能够较为真实的反映实际的装配需求。

该方法的基本原理也可作为框架使用，即根据不同的装配需求和实际情况，可添加其他装配关系密切程度的量化指标，不仅仅局限于提出的三个量化指标，使该方法灵活性大大增强。