作用于转子系统的叠加正弦载荷识别研究

杨 波，杨兆建，杨亚东

（1.太原理工大学机械工程学院，山西 太原 030024；2.煤矿综采装备山西省重点实验室，山西 太原 030024）

1 引言

作为最常见的机械设备，旋转机械在各个制造行业起着至关重要的作用[1]。转子系统是旋转机械的核心部件，其稳定、正常运行关系到旋转机械乃至整个机械设备的安全生产以及操作人员的生命安全[2]。在旋转机械设备中，当转子系统的负载超出其最大承受载荷值，可能会产生严重后果[3]。所以对转子系统的载荷进行识别尤为重要。现有测量技术在某些情况下是无法对转子系统的载荷进行直接测量，而通过电机电流信号可反映出与电机相连的转子系统负载变化[4]。现有的利用电机电流信号进行载荷辨识的研究有，文献[5]提出两种载荷定量识别方法，定量识别出作用在转子系统上的正弦载荷。文献[6]将不同扭振下的电机电流进行频谱分析，运用奇异值分解、小波包分解以及BP 神经网络，识别出作用于转子系统的扭矩激励。而在国内外，大多学者则运用电机电流信号进行机械设备的工况检测以及故障诊断[7-10]。而对多种载荷叠加，尤其是两种不同的正弦波叠加载荷的识别却未见相关研究。

因而提出了叠加载荷的定性与定量识别方法，对作用于转子系统的叠加正弦载荷进行识别。首先对采集的电流信号进行小波分析与处理，与施加于转子系统的叠加正弦载荷信号进行对比，进行载荷定性识别；其次运用希尔伯特模量法，分析出叠加正弦载荷的不同频率，根据不同频率进行滤波，剥离出不同频率的正弦载荷作用下所得电流信号；最后运用支持向量机回归分析方法，在建立起电流与载荷之间隐性关系的基础上，对叠加之前不同的正弦载荷进行预测，实现载荷定量识别。将这一系列识别方法运用于转子系统试验，进行载荷识别，验证定性与定量识别方法的可行性与有效性。

2 载荷定性识别

相较其他信号分析处理方法而言，小波分析可以实现信号的局部分析处理。它能够将低频信息通过长时间窗口得以表征，高频信息通过短时间窗口得以表征[11]。但是短时间获取高频信息就面临着高频分辨率低的问题。针对这一问题，相关学者提出了小波包分解方法，运用二进制方式，对信号进行频率细分，进而使高频分辨率得以提高。此外，小波包分析还可根据所分析信号的特征进行频带自适应，完成与信号频谱的匹配[12]。三级小波包分解树，如图1 所示。它是一个完整的二进制树，该分解树可将信号S表示如下：

式中：A—低频信息；D—高频信息。其后数字表示运用小波包进行分解的层数，也称之为尺度系数。

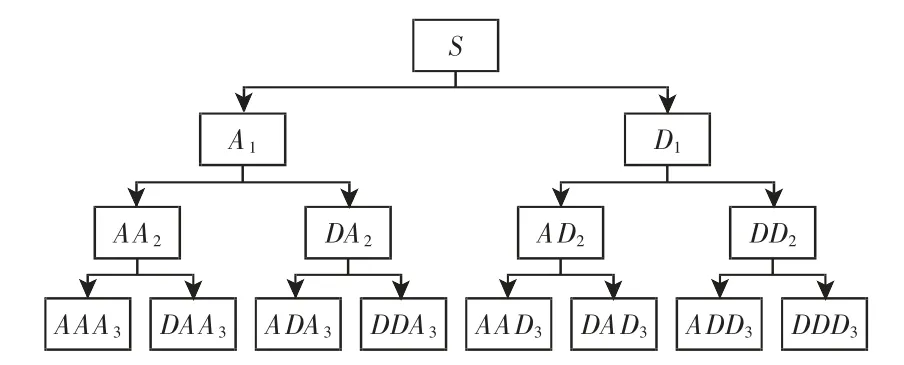
图1 三层小波包分解树Fig.1 Three-Layer Decomposition Tree of Wavelet Packet

在完成小波包分解之后，将分解得到最后一层的系数进行重构，即小波包分解的逆过程，可实现信号的分离。由此可以获取加载于转子系统的载荷信号的特征，与原始载荷信号进行对比，便于对载荷进行定性识别。

3 载荷定量识别

如若已知定性识别出的载荷是由两个不同的正弦信号线性叠加而得，则叠加正弦载荷可假设如下：

那么只需要识别出两个正弦各自的幅值A、B与频率f1、f2，继而进行线性叠加，便可获得叠加后得载荷。在本节，首先运通过希尔伯特模量法，将采集到的时域电流信号转化为频域信号，进行频谱分析，获取两个正弦载荷的不同频率。继而运用FFT 滤波，按照不同频率，剥离对应的电流时域谱。最后建立基于电流与载荷的支持向量机模型，由前述电流时域谱获取电流特征值，利用支持向量机模型进行载荷幅值预测，求出载荷幅值，完成叠加载荷的定量识别。

3.1 希尔伯特模量法

希尔伯特变换可以将连续时间序列s（t）变换为h（t）：

变换后的频率响应为：

由此看出，希尔伯特变换可使得原始信号s（t）相位相差90°，也即h（t）与s（t）构成正交副。将h（t）与s（t）构成解析信号如下：

其中，y（t）的幅值为即为希尔伯特模量[13]。在施加载荷的情况下，采集到的电机电流信号由两部分构成，其中未加载的电流信号为载波信号，施加的载荷为调制信号。作以下假设：

由上式可计算出希尔伯特模量为：

可以看出，原始电机电流信号的基波部分变成了直流分量，而被基波所掩盖的外载荷信号的频率便可得以确定。

3.2 快速傅里叶变换滤波

快速傅里叶变换（FFT）不仅可以实现信号序列的时频域转换，获取信号序列的频率成分以及各频率对应振幅，还可以将频域的某一频率成分振幅置零，进而利用快速傅里叶反变换（IFFT）将频域转换到时域实现滤波[11]。在运用希尔伯特模量法获取叠加载荷中每一正弦载荷的频率之后，通过快速傅里叶变换滤波，继而运用快速傅里叶反变换得到滤去某一频率后的电机电流信号，为后续获取每一正弦载荷的幅值提供便利。

3.3 支持向量机回归预测

支持向量机（SVM）是文献[14]在上世纪90 年代基于统计学理论而提出来的一种新的机器学习方法，该方法运用VC 维理论和结构风险最小化原则，通过非线性变换，将原始变量投射到某个高维空间，转化为线性问题，最终解决非线性问题。相比较其他算法，支持向量机在对样本空间的非线性问题的解决以及高维模式识别上有着很大的优势。运用支持向量机的回归分析，建立起预测模型，可以利用已知的输入信息，根据预测模型，较为精确的预测出未来的输出结果。这一过程主要是对已有的样本集（x1，y1），（x2，y2）…（xn，yn）（其中xi∈Rn，y∈R）进行训练，建立起x与y之间的隐性关系，根据这一关系，在输入x时预测出y的值。在运用支持向量机进行载荷值预测时，首先运用稳态载荷建立样本集，取某一时间区间内的载荷与电流信号特征点作为训练学习的原始数据，建立起载荷与电机电流的关系模型。对于正弦载荷的识别，可运用电机电流时域图的包络线峰值与谷值对应的电流特征值，进行支持向量机预测，获取对应的载荷大小。此时所得到的是正弦载荷的最大值C+A、C+B与最小值C-A、C-B，通过联立方程可以解出A、B以及C的大小，结合希尔伯特模量法识别出的频率，便可识别出叠加正弦载荷大小，完成载荷识别。

4 试验与分析

4.1 试验平台建立

转子系统试验台由三相异步电机、转子系统（轴承、轴、转盘等）、磁粉制动器、底座、调速器、信号发生器、信号采集分析仪、电流变送器等组成。首先，利用计算机控制信号发生器产生两个正弦叠加后的载荷信号，将该信号用来控制磁粉制动器进而对转子系统施加载荷，载荷值为T=0.3sin（4πt）+sin（2πt）+5Nm。利用变速器，连接数据采集分析仪，将数据采集分析仪通过USB 连接到计算机，利用DASP 软件进行数据采集分析仪的设置以及数据采集与MATLAB 格式导出。试验时，利用调速器控制电机转速为1500r/min，将采样频率设置为5000Hz。试验台构造，如图2 所示。

图2 转子试验台Fig.2 Rotor System Test Bench

4.2 载荷定性识别

叠加正弦载荷作用下的电机电流信号时域图，如图3 所示。试验过程中由于所施加载荷频率低，所以在进行定性识别时可只使用小波分析。在小波分析之前，需要将三相交流电转变为等效直流电，转换公式为对等效直流电时域信号进行小波分解与重构，如图4 所示。通过对比信号发生器产生的叠加正弦信号（图5（b））与第6 层的低频系数进行重构后的叠加载荷信号（图5（a）），可以确定该叠加载荷信号即为两个正弦载荷线性叠加之后的载荷，完成了载荷的定性识别。

图3 叠加正弦载荷作用下电机电流时域图Fig.3 Motor Current Signal Time-Domain Diagram Under Superposed Sinusoidal Load

图4 6 层小波分解及重构Fig.4 Six-Layer Wavelet Decomposition and Reconstruction

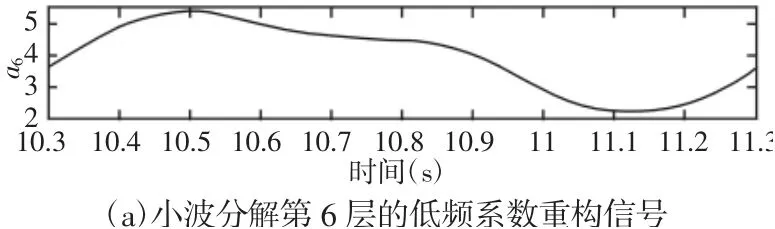
图5 信号对比Fig.5 Signal Comparison

4.3 载荷定量识别

在试验过程中，首先对施加了稳态载荷的转子系统的电机电流信号进行采集，通过稳态载荷建立样本集，建立载荷与电机电流之间的关系，如表1 所示。

表1 载荷与电机电流关系Tab.1 Relationship Between Load and Motor Current

在进行叠加的正弦载荷进行定量识别过程中，起初对采集到的电机电流进行希尔伯特模量法处理，得到载荷的频率为1.005Hz和2.009Hz，也即两个正弦载荷在未进行线性叠加之前各自的频率，如图6 所示。继而运用快速傅里叶变换滤波方法，分别滤去1.005Hz 和2.009Hz 后的电机电流信号，如图7 所示。在滤去1.005Hz 成分的电流信号中，采集到的电流峰谷值为3.123A 和2.471A，通过支持向量机预测的载荷值为5.098Nm 和4.464Nm；在滤去2.009Hz 成分的电流信号中，采集到的电流峰谷值为3.854A和1.801A，通过支持向量机预测的载荷值为5.79Nm 和3.804Nm。

图6 叠加正弦载荷频率Fig.6 Frequency of the Superposed Sinusoidal Load

图7 频率成分被滤除之后的电机电流信号Fig.7 Motor Current Signal after Frequency Component is Filtered

由上述数据可以列出方程组如下：

解上述方程式组可得：A=0.317，B=0.993，C=4.789。

通过定量识别出的载荷为：

比较了真实载荷与定性定量识别得到的载荷，如图8 所示。由定量识别结果以及图8 可以看出，运用希尔伯特模量法所还原出的频率与真实载荷的频率几乎完全相同。在幅值上，运用支持向量机预测得到的幅值与真实载荷的幅值有一定的误差，但是误差较小，识别精度较高。

图8 识别所得载荷与实际载荷的对比Fig.8 Comparison Between Identified Load and Actual Load

5 结论

（1）通过分析电机电流信号，对施加于转子系统的两个正弦信号线性叠加后的载荷进行识别。针对载荷识别，提出了一种定性定量识别方法，最后进行试验验证，说明识别方法的可行性与准确性。（2）载荷定性识别采用了小波分析方法对信号进行分解以及底层节点进行系数重构，将重构后所得到的时域图与信号发生器产生的信号进行比对，判断出载荷是由两个正弦信号线性叠加之后得到的新的叠加正弦载荷。（3）载荷定量识别采用了希尔伯特模量法确定叠加载荷的两个正弦成分的频率；采用快速傅里叶变换滤波对电机电流信号按照两个不同的频率进行滤波，获得包含有两个不同频率载荷激励的电机电流信号；采用支持向量机预测两个电机电流信号的特征值所对应的载荷幅值与相位。通过运用此方法识别出的载荷相比较实际载荷来说识别结果误差较小，准确度较高。（4）在定性识别过程中存在着定性不准确的可能，将定性与定量识别方法结合起来，可以更加准确地识别出载荷的类型与大小。