架空裸导线截面应力分析

李培生，熊 捷，刘国平，高 超

（南昌大学机电工程学院，江西 南昌 330031）

1 引言

架空裸导线以钢芯铝绞线（ACSR）为主，它由钢芯和铝股绞制而成，其中铝的导电性能好、重量轻、成本低，所以外部铝股负责传送电能；中芯由钢制成，它提供了足够的强度使延展性更高的铝不被拉伸，这给输电线提供了很好的整体抗拉强度[1]。钢芯铝绞线内部相邻层绞线旋向相反且各层股线捻角从内到外依次增大。钢芯铝绞线运行时受轴向拉伸，线内钢丝与铝丝会产生相对滑移与摩擦，从而导致钢芯铝绞线截面各丝应力分布不均。而现有的结构分析中为了简化模型，通常忽略钢芯铝绞线内相对滑移与摩擦影响，假设截面等应力分布，这不符合钢芯铝绞线的实际受力情况。精确的研究钢芯铝绞线应力分布情况，对钢芯铝绞线结构设计及优化、疲劳寿命预测、断线事故分析提供重要的理论依据，对输电线路稳定性的提高及经济效益的增加具有重要意义[2、5、14]。因此国内外众多学者对钢芯铝绞线的力学特性进行了研究。文献[1]利用梁有限元和实验方法研究了受拉力作用的钢芯铝绞线的线性弹性静力学分析模型，文献[3]利用数值模拟方法给出了钢芯铝绞线的刚度，耦合刚度和弹性模量数学模型，文献[6]利用三维模型对钢芯铝绞线进行了分析，但只考虑了线股之间接触特性。

以某水电站Ⅱ回220KV 工程线路所使用的LGJ-240/40 钢芯铝绞线为实际对象建立几何实体模型，研究其截面应力分布规律及线内各丝之间相对滑移与摩擦对截面应力分布的影响。最后将仿真结果与已有文献的数值计算结果和实验结果进行对比，验证了分析结果的正确性。

2 模型构建

2.1 实体模型构建

LGJ-240/40 钢芯铝绞线的结构参数，如表1 所示。其中绞线最外层为右旋，相邻层绞线旋向相反。螺旋线的展开图，如图1 所示[7]。基于对称性计算时钢芯铝绞线长度取最外层绞线节距的1/4为64.98mm，在SolidWorks 中按照表1 的几何尺寸建立实体模型，如图2 所示。

线股缠绕方向轴心线与轴线方向所成的夹角称为捻角以βi表示，其捻角的计算公式为：

式中：Li—节距；di—直径；Di—第i层股线外径。

表1 LGJ—300/25 型钢芯铝绞线规格（GB1178-83）Tab.1 Specification for LGJ300/25 ACSR（GB1178-83）

图1 线股展开示意图Fig.1 Diagram of the Unfolded Wire

图2 钢芯铝绞线结构实体模型Fig.2 Entity Model of ACSR

2.2 有限元模型的建立

将模型导入ANSYS Workbench 中，根据[9-10]给出的电源线材料特性，钢丝的杨氏弹性模量为207GPa，泊松比为0.28；铝丝杨氏弹性模量为69GPa，泊松比为0.33。

使用8 节点实体单元Solid185 单元进行网格划分。由于网格太大会导致模型计算精度差，无法收敛；网格太小又会使计算时间太长，为了兼顾计算精度与计算效率，本模型将钢芯铝绞线轴向网格长度控制为3.249mm（轴向长度20 等分），定义端面单根铝丝与钢丝单元沿直径10 等分：钢丝截面单元大小为（0.266×0.266）mm2，铝丝为（0.342×0.342）mm2，网格划分后生成81925 个节点和66432 个单元。

图3 有限元网格模型Fig.3 Finite Element Mesh Model of ACSR

3 钢芯铝绞线内部各丝之间无相对滑移及摩擦时截面应力分布情况

钢芯铝绞线内部各丝之间无相对滑移及摩擦时，导线运行中两端悬挂在杆塔上，所以约束导线一端（Y=0）平面的X、Y、Z方向上自由度。由于其轴向为对称拉伸，所以创建一个远端点并与钢芯铝绞线另一端面（Y=64.98）关联构成刚域面使端面各条线股的径向和轴向位移相同。根据GB1179-1999 中钢芯铝绞线的计算拉断力（RTS）为83370N，因为我国架空输电线路运行张力一般为（15～25）%RTS，所以对端面刚域面分别施加15%RTS、20%RTS、25%RTS 的集中载荷，分析钢芯铝绞线中间截面（Z=32.49）的应力分布规律。

当施加的端面载荷为16674N（20%RTS）时，LGJ-240/40 钢芯铝绞线中间截面等效应力分布云图，如图5 所示。钢芯铝绞线截面内的等效应力整体上呈现出圆环状分布，由于钢丝与铝丝杨氏弹性模量相差较大，钢丝应力明显大于铝丝应力。同层铝丝和同层钢丝的单丝等效应力分布情况几乎相同。钢芯铝绞线邻层挤压力会产生累加效果，材料相同时等效应力随层数增加而略有减小，内层钢丝应力略大于外层钢丝应力，相似的内层铝丝应力略大于外层铝丝应力。同一层内应力相对较大区域出现在靠近轴心内侧，钢丝、铝丝接触的部位、外侧丝与内侧丝接触部位。内部钢丝截面等效应力约为147MPa 左右，且由中心向外缓慢递减，单丝截面等效应力呈扇形分布，相似的各层铝丝截面等效应力约为48MPa 从靠近中心部分向外层逐渐减小并呈扇形分布。钢芯铝绞线Y轴方向的轴向应力变化不大，截面铝丝呈现均匀分布大小为45MPa 左右，第二层钢丝呈半圆分布内侧与外侧为126MPa左右变化并不大。钢芯铝绞线截面沿径向等效应力分布曲线，如图6 所示。x轴为钢芯铝绞线截面上某点距离中心钢丝圆心的距离r，y轴为以r为半径同心圆上节点的平均等效应力。靠近圆心位置的钢线等效应力基本不变，而到钢丝层与铝丝层交接位置附近应力突然大幅度下降，到铝丝层位置之后曲线十分平滑，最外层略有减小。

图4 20%RTS 时Y 轴方向应力Fig.4 Y Axis Direction Stress at 20% RTS

图5 20%RTS 时Y 轴等效应力Fig.5 Y-Aaxis Equivalent Stress at 20% RTS

图6 钢芯铝绞线（Y=32.49mm）节点等效应力Fig.6 Stress of Cross-Section at End of ACSR（Y=35.64mm）Under Tensile Force

为验证有限元仿真结果的准确性，将所得结果与文献[8]数值分析结果进行对比：

式中：zi—第i层线股数量；E—杨氏弹性模量；v—泊松比；β—捻角；A—股线的截面积；F—载荷。下标i和k指的是特定层数，从里层到表层，第一层为n=0。

表2 两种方法求得截面应力值Tab.2 Two Methods to Obtain Sectional Stress Value

表中：σyk—理论计算所得各层轴向应力；σY—分析所得各层股线轴向平均应力。

表3 两种方法求得截面应力误差Tab.3 Two Methods to Obtain Sectional Stress Error

由表3 可得两种结果误差δn：

表3 可知两种方法所得结果误差在（-3.368～0.96）%之间，因此可认为这里所的仿真分析结果是正确的。

4 钢芯铝绞线内各丝之间存在相对滑移及摩擦影时截面应力分布情况

在线路实际运行受载情况下，钢芯铝绞线内各钢丝、铝丝之间存在相互接触、摩擦与挤压作用，其过程极其复杂，钢丝、铝丝之间的接触对钢芯铝绞线的整体性能、局部应力场具有重要影响，在接触摩擦力作用下，钢芯铝绞线截面应力分布将发生很大变化，其中摩擦会降低钢芯铝绞线的强度和寿命，所以研究钢芯铝绞线内部各丝之间的相对滑移、摩擦是十分必要的。采用Targe170 和Conta174 单元进行摩擦分析，接触面相互作用模型采用可法向分离，切向滑动，设定铝-铝和铝-钢的摩擦系数为0.5，钢-钢的摩擦系数为0.3[11、13]，采用Augmented—Language 法计算线内各丝之间的接触[12]。

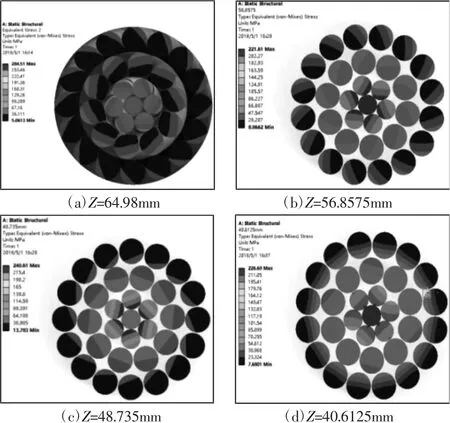
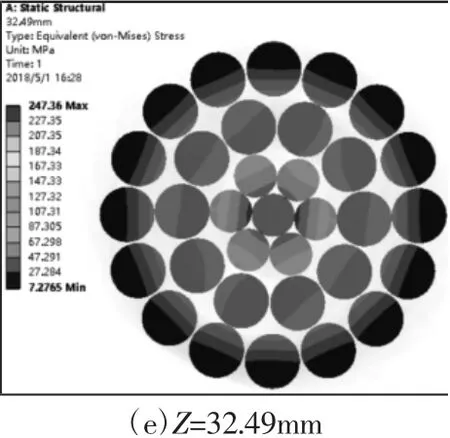
图7 F=20%RTS 时轴向载荷作用下钢芯铝绞线截面等效应力Fig.7 Equivalent Stress of ACSR Cross-Section Under Axial Load at F=20% RTS

在F=20%RTS 载荷作用下钢芯铝绞线考虑丝间相对滑移及摩擦后的多个等距截面等效应力，如图7 所示。线内各丝在相对滑移及接触摩擦力作用下，截面等效应力分布将发生很大变化。由图7（a）～图7（c）可以看出钢芯铝绞线捻向与捻角对等效应力分布影响显著，其截面等效应力伴随着捻角变化呈交错螺旋形分布。观察图7（d）、图7（e）并与图7（a）～图7（c）对比可知，等效应力随着与端面距离的增加由螺旋分布向不规则的中心对称分布转变，铝丝层等效应力由靠近中心内测向外侧递减。由中间截面云图可看出各丝的等效应力分布与各层钢丝或铝丝所在位置有关，截面内与邻层相接触钢丝或铝丝应力大于同层其他丝。

图8 钢芯铝绞线（Z=35.64mm）节点等效应力Fig.8 Equivalent Stress of Steel-Cored Aluminum Strand（Z=35.64mm）Joints

为进一步研究钢芯铝绞线内部股线之间相对滑动及摩擦影响的截面应力分布情况，建立钢芯铝绞线截面沿径向等效应力分布曲线，如图8 所示。从图8 可以看出在钢芯铝绞线截面上，中心钢丝部分等效应力明显大于外侧铝丝等效应力，其比值约为5：1。随着点到圆心距离的增加总体上依然是钢丝等效应力远大于铝丝等效应力，但钢芯等效应力值比不考虑滑移和摩擦时发生了较大变化，其中钢芯增加了60MPa 左右，内层铝丝增加了10MPa左右，而外层铝丝则有所减小。

为进一步验证有限元模型的正确性，建立LGJ-300/25 钢芯铝绞线模型，同样取最外层节距的1/4 长度71.28mm，弹性模量泊松比、接触单元、算法沿用上文提供的参数进行分析，将分析结果同文献[14]得到钢芯铝绞线实验数据进行对比，如表4 所示。相对误差计算如下：

由上表可知仿真结果与实验结果基本一致，误差在3%左右且随着载荷增加误差不断减小，由上述结果表明，可认为分析结果是正确的。

表4 两种方法求得截面应变及误差Tab.4 Two Methods to Obtain the Cross-Section Strain and Error

5 结论

（1）当不考虑钢芯铝绞线内各丝之间相对滑移时，钢芯铝绞线受到轴向拉伸载荷和邻层、同层钢丝或铝丝的挤压力作用，导致钢芯铝绞线截面应力分布不均，整体呈圆环状分布，而材料的不同决定了中心钢丝应力远大于外侧铝丝应力，钢芯与铝股等效应力比值约为3：1，Y轴方向应力变化不大，基本呈现均匀分布。（2）当考虑钢芯铝绞线内各丝之间相对滑移及摩擦时，端面应力分布主要由钢丝或铝丝的旋转方向和角度决定，所以靠近端面的截面等效应力呈交错螺旋分布，靠近中间截面应力由于受到丝间相对滑移、摩擦、挤压力共同作用，应力呈中心对称分布。钢芯铝绞线内外层材料不同使钢芯层应力依旧远大于外侧铝股，其比例约为5：1。同时与不考虑线内各丝相对滑移结果相比各层应力值有所改变，应力分布情况也更加复杂。（3）将钢芯铝绞线仿真结果同计算值与试验值比较，可以看出结果基本吻合，验证了模型的正确性。对载荷条件下钢芯铝绞线进行仿真分析，计算得到了载荷作用下截面应力分布情况，为进一步开展载荷作用下钢芯铝绞线寿命预测、断线事故的分析提供了理论依据。