基于 MATLAB 的数学课堂信息化实践

◇ 福建 杨昔阳 孙伟婧

随着信息技术的发展，结合信息技术手段进行课堂教学已经成为一种重要的教学方式.本文通过分析传统课堂教学方式的弊端，说明了在课堂教学中引入信息化教学实践的必要性，并通过MATLAB 的用户图形界面，以定积分和旋转曲面为例介绍在课堂教学中采用信息技术课件进行教学的方法和优点.

数学是一门历史悠久的学科，近些年，随着计算机技术的迅猛发展，数学与信息技术形成了相辅相成的局面.一方面，数学学科越来越成为现代科学技术发展的重要工具；另一方面，一些原本难以通过课堂板书和语言呈现的数学知识，很容易通过信息化工具加以呈现，大大提高了数学知识的教学和传播.

传统的数学教学模式采用“粉笔＋黑板＋PPT”的形式，依靠教师语言、板书和幻灯片完成课堂教学.由于这些教学手段难以调动学生学习的积极性，与学生的互动比较少，因此一些抽象的数学知识概念，很难通过这些教学手段有效教学.笔者认为结合MATLAB等现代信息技术手段，可以丰富这些抽象的数学概念的教学手段，激发学生学习兴趣，通过有效的演示和互动达到较好的教学效果.

1 传统课堂教学模式弊端

虽然传统教学模式在一些知识和技能的传授上有其独特的优势，但是对于某些抽象的数学概念，这些教学方法就显得力不从心了.本文先对传统的教学模式的缺点进行简要总结，从而说明引进信息技术手段的必要性.

1.1 缺乏直观性和表现力

根据神经生物学家和教育心理学家的研究：人类对知识信息的接受，70%来自图象视觉.抽象的数学概念、定理的主要呈现方式是文字和教师的讲解，但这些方法无法让学生直观地观察到这些概念和定理的本质和变化规律，它们非常依赖学生的数学抽象素养，基础较差的学生很难通过教师的描述构建这些概念的正确结构和模型，对知识的理解只能停留在表面.例如，在讲解旋转曲面形成的过程中，部分学生就很难在脑海中想象曲线在立体空间旋转后所构建的曲面.

1.2 缺乏趣味性和创造性

传统的数学教学模式是教师占主导地位，教师在课堂教学中通过对概念、定理、定义、公式的反复讲解将知识灌输给学生.这个过程缺少学生的亲身参与，一些数学基础较差的学生就很容易感到疲倦，难以集中注意力理解教师的授课内容，极大降低了课堂的教学效率和趣味性.为了消除这种情况，教师应该减少灌输式的授课方式，以多种方式进行课堂教学，并尽可能增加学生参与课堂教学的机会.

1.3 不利于教师的发展

在信息技术蓬勃发展的大背景下，具有一定的信息素养已经成为教育的一个重要目标.相应地，数学教师也应该与时俱进，学习新的信息技术手段，通过基于信息技术的课件制作，体会数学的作用和应用，创新数学教学活动.缺乏成长的教师必然会与时代脱节，无法适应日新月异的教学改革要求，容易形成职业倦怠，这些后果势必会对课堂教学的效果形成不利的影响.

2 基于MATLAB的课堂教学素材开发案例

MATLAB是美国MathWorks公司开发的一款数学软件，它在科学运算、图象展示、算法验证与实现以及用户图形界面开发等方面具有巨大优势.它的编程语言十分接近自然语言，也符合数学表达式的表达规范，入门门槛比较低，即使对计算机编程不熟悉的数学教师，也能在短时间内学习和掌握.与其他信息技术手段相比，利用MATLAB来辅助一些数学概念教学的数学课堂更加具有针对性，对培养学生的综合素质也更具优势.本文通过一些案例来说明MATLAB在定积分、旋转曲面概念的教学方面的具体应用.

2.1 定积分的教学案例

在传统的教学过程中，教师对定积分的讲解一般是通过概念的分析配合绘图说明.借助MATLAB 的用户图形界面，教师可以通过简单的编程，利用所开发的用户图形界面的交互功能来设计定积分的概念教学，教学过程如下.

1)在开展教学之前，设计相关的用户图形界面，所制作的课件应该包含“分割－近似—求和—取极限”等操作.

2)在课堂教学中，教师结合制作好的用户图形界面，讲解“分割—近似—求和—取极限”的近似过程.教师通过这个用户图形界面，就很容易说明一段曲线下方的面积，可以由小长方形近似，随着分割点的个数(小长方形的个数)逐渐增加，各个小长方形面积之和将越来越接近整条曲线下方的面积，从而使得学生对定积分的概念有了形象的理解.例如，图1 给出了f(x)＝sinx 在区间(0，)上的定积分与长方形面积之和的关系.

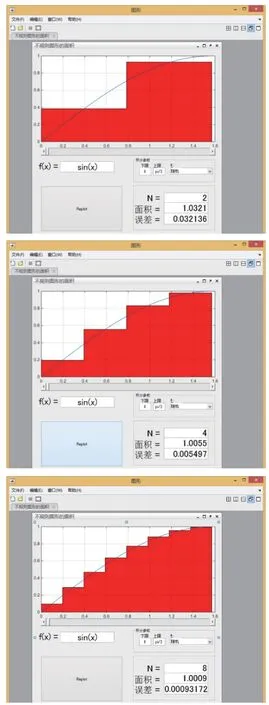
图1 定积分定义的教学举例

3)教师可以让学生自己动手进行操作，改变函数的形式和积分上下限，修改长方形的个数N，观察随着N 的改变，长方形面积之和与曲线下方所包围面积的误差值的变化.通过这个实践，学生亲身感受到“分割”越细化，长方形的总面积与所求面积就越接近的极限思想.

4)教师还可以通过这个用户图形界面，让学生体会长方形面积的近似方法(即长方形高度的选取方法)对实验结果的影响(如图2所示).学生通过实践将发现：当长方形的个数N ➝＋∞时，长方形的近似方法对于结果不产生影响，从而体会到了“分割—近似—求和—取极限”这个过程的合理性.

图2 长方形近似方式的选取方式

2.2 旋转曲面的动态演示

旋转曲面是中学数学和高等数学重要的教学内容，旋转曲面的授课十分依赖学生的空间想象能力，曲面的形成过程较为复杂，教学过程较为抽象.利用MATLAB的用户图形界面，学生就能够直观地观察到旋转曲面的形成过程.同时还可以通过3D 的拖拽，从各个角度观察所得的旋转曲面，教学过程如下.

1)在开展教学之前设计用户图形界面，所制作的课件应该包含旋转轴、旋转曲线等基本要素的操作.

2)在课堂教学中，教师结合制作好的用户图形界面，讲解旋转曲面的形成过程(如图3所示).教师让学生想象一条旋转曲线围绕一条旋转轴旋转的图象.通过演示，学生可以验证自己的想象结果和图象的形成结果是否一致.

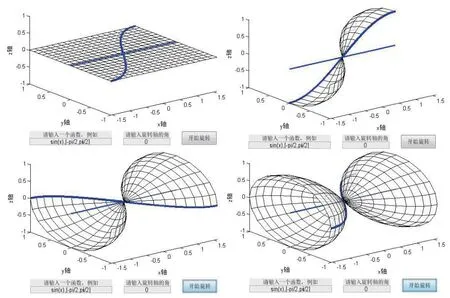
图3 旋转曲面的形成过程

3)教师可以通过MATLAB 的3D 旋转功能，直接对图象进行拖拽、旋转.让学生从不同角度观察形成的旋转曲面，在脑海中形成准确的旋转曲面的立体图形(如图4所示).

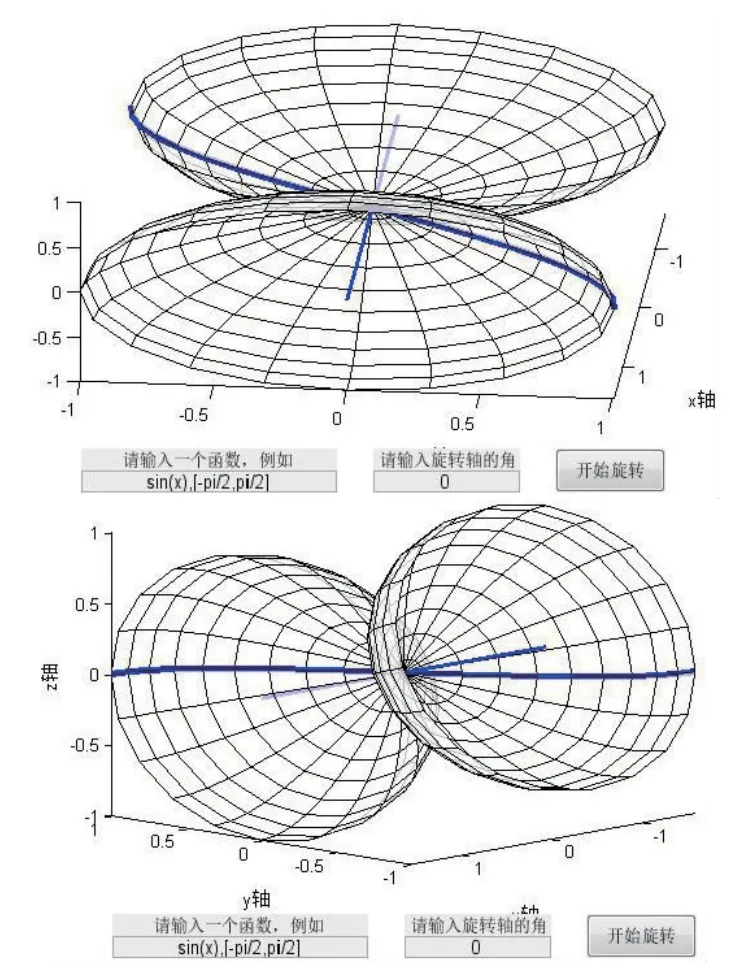
图4 旋转曲面不同角度视图

4)由学生充分发挥自己的创造性和想象力，选择自己喜欢的函数形成旋转曲面，先想象旋转曲面的图象，再动手操作，观察旋转曲面的形成过程.

3 小结

以信息技术为辅助手段的教学手段正在逐渐成为数学课堂教学的主流.通过信息技术手段辅助教学有助于活跃课堂气氛，提高学生课堂参与的兴趣，也能提高教育质量和教学效果.MATLAB 为数学教师在课堂教学中制作信息技术教学课件提供了便利，使一些难以用传统方式呈现的抽象数学概念，可以以一种形象的方式展现在学生的面前.MATLAB 的用户图形界面具有较强的灵活性，教师可以根据班级学生的情况为用户图形界面增添不同的组件和操作.此外，教师可以在教学过程中安排学生亲身参与用户图形界面的演示，这种实践活动有助于学生调动多种感官学习抽象的数学概念.

值得注意的是，教师利用MATLAB 制作这样的课件时，自身要对 MATLAB 有充分的了解.MATLAB的编程能力需要在不断的实践中逐步锻炼和提高.此外，教师也应该对所教授的数学概念有充分的了解，为学生按需定制具有合适操作步骤的课件.