绕单轴旋转的固面可展开天线展开过程研究
徐 彦,成 强,黄 河,周 鑫,李 明
(1.中国航天科技集团有限公司空间结构与机构技术实验室,上海201108;2.浙江大学航空航天学院,浙江杭州310027;3.西北工业大学力学与土木建筑学院,陕西西安710072)
固面反射面因具有非常高的型面精度而广泛应用于卫星的口径天线。然而,固面反射面的结构形式导致其口径尺寸受到限制及收纳性能较差,进而无法提高天线的增益,影响天线的适用范围。采用固面反射面可展开的形式能有效增大其口径和提高其收纳性能。
目前,可展开固面反射面天线大多采用以中心对称的花瓣式旋转收纳的可展开结构形式[1-7],其收纳比可降低至0.3~0.4[1]。其中,大型花瓣式空间望远镜(large petal-type space mirror,LPSM)模型[3]和新型花瓣式可展开固面反射面天线(new petal-type de-ployable solid surface antenna,NPDSSA)[1]采用的是完整单叶片沿正交双轴展开的形式;美国汤普森·拉莫·伍尔德里奇(简称TRW)公司研发的花瓣式可展开(extended flower)天线模型[8]和固面可展开天线(solid surface deployable antenna,SSDA)模型[9]采用的是叶片通过多个铰链实现折叠和展开的形式。上述模型和天线的每一个叶片都有2个甚至更多的转动副,这导致可展开结构的可靠性较低。而俄罗斯列别捷夫物理研究所天文空间中心(Astro Space Cen-ter of Lebedev Physical Institute)提出的10 m口径光谱-M太空望远镜[10]的可展开反射面采用完整单叶片绕单轴旋转的方式,减少了转动副的数量,从而提高了可展开结构的可靠性。
基于单叶片绕单轴旋转的原理,笔者主要探究了花瓣式可展开固面反射面天线叶片绕正交双轴旋转展开和绕单轴旋转展开的对应关系及相应的设计方法,并通过实例验证其展开过程,旨在为绕单轴旋转展开的固面反射面的设计与分析提供参考。
1 绕双轴旋转与绕单轴旋转的等效变换设计
绕正交双轴旋转的固面可展开天线[1]以叶片自身的对称轴和与中心圆盘边缘相切的轴线为2个正交的旋转轴进行展开:先绕叶片自身的对称轴旋转θ,再绕与中心圆盘边缘相切的轴线旋转ω,最终展开到位。如图1所示,将抛物反射面分割成中心圆盘和环向等分的抛物面叶片,曲面CDFE是以平面XOZ为对称平面的主要参考叶片,中心圆盘在平面XOY上的投影半径为r,完整抛物反射面在平面XOY上的投影半径为R,则参考叶片在平面XOY上的投影半径的范围为[r,R]。定义与中心圆盘边缘相切的轴线A1A2到中心圆盘顶点O在X方向的投影距离为m,沿Z方向到抛物面的距离为a;叶片自身的对称轴B1B2的中心沿X方向的投影距离为l,沿Z方向到抛物面的距离为b。
根据Euler定理,任意一种旋转变换都可以归结为若干个绕坐标轴旋转的组合。因此,通过坐标变换,将上述叶片先后绕2条正交轴线B1B2和A1A2的旋转转化为绕空间内某个轴线矢量n=(nx,ny,nz)T旋转φ,得到等效的展开结果。
在参考叶片CDEF旋转到C'D'E'F'的过程中,通过坐标的旋转变换,在考虑||n||=1的情况下,可得单轴轴线矢量n、单轴旋转角φ与双轴旋转角θ、ω之间的关系为:
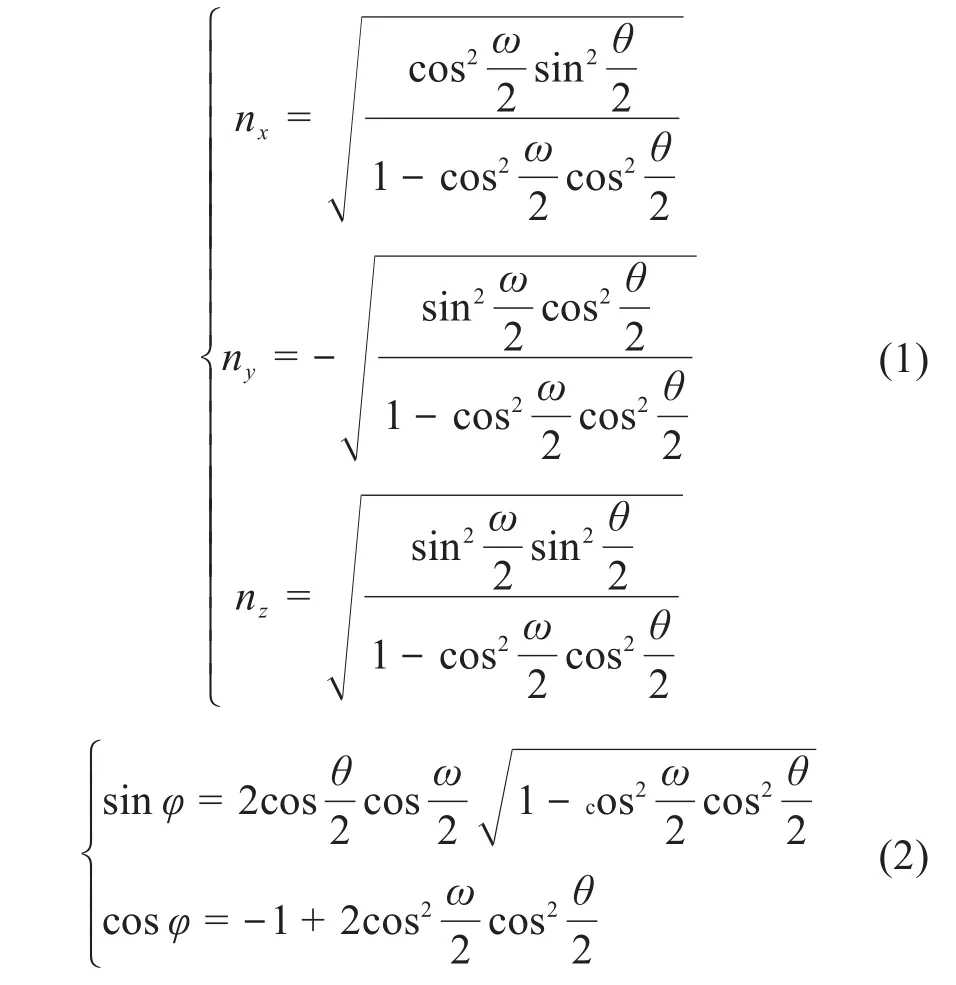
式(1)还可以表示为:(x-x0)/nx=(y-y0)/ny=(z-z0)/nz=p,其中点(x0,y0,z0)在该轴线上。
设叶片CDEF上任意一点M的初始坐标为(xM,yM,zM),通过文献[1]中的双轴旋转坐标公式可求得旋转后叶片C'D'E'F'上点M'的坐标为(xM',yM',zM'),M点在单轴轴线上的垂足H的坐标为(xH,yH,zH)。由相应几何关系可知,矢量MH垂直于该单轴轴线矢量n,且点M和点M'到垂足H的距离相等,则可得待求轴线上点的坐标,即由轴线矢量n和轴线上某一点的坐标即可确定该单轴在空间中的位置。因此,通过式(1)和式(2)可以将绕正交双轴旋转展开等效变换为绕空间内某一单轴旋转展开。
2 绕单轴旋转的固面可展开天线展开实例
基于上述绕双轴与单轴旋转的等效变换设计原理,设计了一个10 m口径星载固面可展开天线。该天线反射面的抛物面方程为x2+y2=12 000z,其焦距f=3 000 mm,反射面半径R=5 000 mm,中心圆盘半径r=1 600 mm,叶片数N=20,则π/N=9°;参考叶片的设计参数为:a=120 mm,b=120 mm,m=1 200 mm,l=2 400 mm。当叶片绕双轴旋转展开时,首先绕轴线B1B2旋转 -45°,再绕轴线A1A2旋转-75°,即θ=-45°,ω=-75°。
叶片CDEF的4个角点的初始坐标为:C(4 938.44,-782.17,2 083.33)mm,D(4 938.44,782.17,2 083.33)mm,E(1 580.30,-250.30,213.33)mm,F(1 580.30,250.30,213.33)mm。由文献[1]中双轴旋转坐标公式可求得4个角点旋转后的坐标为:C'(108.55,665.50,4 162.77)mm,D'(1 177.02,1 771.66,3 876.48)mm,E'(879.92,-280.69,479.48)mm,F'(1 221.83,73.28,387.87)mm。
将θ=-45°,ω=-75°代入式(1)和式(2)中,可得:n=(0.446 299,0.826 765,0.342 457)T,φ=-85.73°。
再从C、D、E、F中任意选取其中2点(x1,y1,z1)、(x2,y2,z2),并根据第1节所述的几何关系建立6个方程,联立方程组可求得所选2点在单轴轴线上垂足的坐标为:(x1H,y1H,z1H)=(1 876.7,1041.3,855.2)mm,(x2H,y2H,z2H)=(1 230.2,-156.3,359.1)mm。
由此可以确定单轴在空间内的位置以及参考叶片绕该轴线的旋转角度φ,最终得到固面可展开天线绕单轴旋转的等效模型。
3 绕单轴旋转的固面可展开天线展开过程的验证
根据上述实例,建立固面可展开天线的ADAMS(automatic dynamic analysis of mechanical systems,机械系统动力学自动分析)模型。以单一叶片完全展开状态作为初始状态,分别绕双轴旋转和单轴旋转完成收拢。叶片绕双轴旋转和单轴旋转的收拢过程如图2和图3所示。通过对比参考叶片的最终收拢状态可知,绕单轴旋转模型的展开效果等效于绕双轴旋转模型,说明本文的设计方法是可行、有效的。
固面可展开天线绕单轴旋转的展开过程如图4所示,由电机驱动各旋转轴展开叶片。结果显示各叶片之间无相互干扰且展开过程平稳。
在同样的外力和展开条件下,在天线绕单轴旋转和双轴旋转的展开过程中铰链受到的力和扭矩的变化曲线分别如图5和图6所示。在天线绕单轴旋转展开的过程中,每个叶片只有1个铰链,而绕双轴旋转展开过程中每个叶片有2个铰链。由图5(a)和图6(a)可知,尽管绕单轴旋转展开时在展开的后半程铰链所受的力略大于绕双轴旋转展开时任一铰链所受的力,但是双铰链的构造导致绕双轴旋转时在2个铰链位置处产生了作用力及初始突变峰值,这大大降低了固面可展开天线的整体可靠性。对比图5(b)和图6(b)可知,虽然绕单轴旋转展开天线中叶片上的铰链所受扭矩也大于绕双轴旋转展开天线中叶片上任一铰链的扭矩,但绕双轴旋转展开天线的2个铰链均承受与绕单轴旋转展开同一数量级的扭矩,因此绕双轴旋转展开天线中的铰链所承受的扭矩更大,对展开过程产生了一定的影响。

图2 参考叶片绕双轴旋转的收拢过程Fig.2 Folding process of reference blade rotating along two axes

图3 参考叶片绕单轴旋转的收拢过程Fig.3 Folding process of reference blade rotating along a single axis
从多体运动的角度分析,相较于绕双轴旋转,绕单轴旋转大大减少了刚体和转动副的数量,在保证结构平稳展开的基础上,大幅度降低了多运动副间的作用力,提高了这类可展开结构的展开可靠性。
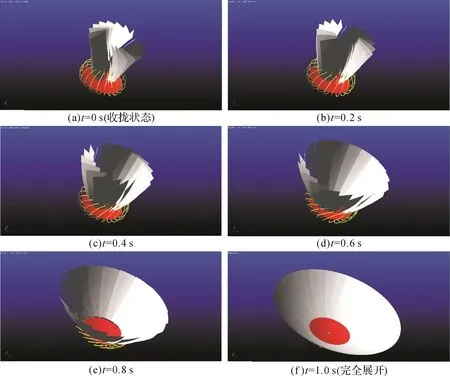
图4 固面可展开天线绕单轴旋转的展开过程Fig.4 Deploying process of solid-surface deployed antenna rotating along a single axis

图5 天线绕单轴旋转展开过程中铰链的受力Fig.5 The force on the hinge during the deploying process of antenna rotating along a single axis

图6 天线绕双轴旋转展开过程中铰链的受力Fig.6 The forces on the hinges during the deploying process of antenna rotating along two axes
4 结论
通过绕双轴旋转与绕单轴旋转的等效变换设计,将目前广泛应用的绕正交双轴旋转的固面可展开天线简化成绕单轴旋转的等效形式,并提出了简单可行的设计方法,减少了花瓣式旋转固面可展开天线的转动副数量,提高了天线结构的整体稳定性和展开可靠性,降低了天线的设计难度与制造成本,这对固面可展开天线的设计和分析有重要的参考价值。

