基于深度图像的实时手势识别方法
时梦丽,张备伟,刘光徽
(南京财经大学 信息工程学院,江苏 南京 210023)
0 引 言
手势识别系统被用作人和计算机系统之间交互的良好界面[1],可让人们以一种更为直接、快捷的方式实现人机交互。因此,手势识别逐渐成为人机交互领域的一个研究热点。
传统传感器(数据手套[2]、鼠标[3]、摄像机[4]等)可捕捉手势信息并进行识别。数据手套可直接获得手势的三维信息,但数据手套的穿戴及位置跟踪器的配置较为复杂,给使用者带来诸多不便。利用跟踪技术跟随硬件设备获取手势路径也可实现手势识别,但此类方法仅适用于手势较为简单的情况,当手势过于复杂时则会导致识别精确度降低。普通摄像机也可采集图像信息进行识别,但此类方法对光照条件、人体肤色较为敏感,易受到环境变化的影响,系统鲁棒性不高。
3D传感器的出现,使得基于手势的人机交互系统取得了进一步的成功,微软的Kinect设备就是其中的代表之一[5]。目前,已有很多学者探讨实现了基于Kinect设备的手势识别[6-8,11]。田元等[6]利用Kinect设备获取深度数据和骨骼位置信息,将指尖点个数、距离等特征量化为六级分类标准实现了数字手势1-10的识别。袁方剑等[7]利用深度图像,结合指尖数目和面积比例实现了“抓取”动作的识别。Wang等[8]将手势的纹理和深度信息以超像素的方式表达,结合EMD距离实现了数字手势的判定。赵飞飞等[9]提取三维骨骼节点坐标,并结合DTW算法实现了简单的“鼠标手势”识别。
本文提出了一种基于Kinect的实时手势识别算法。该算法利用Ostu阈值分割法分割手势,提取一系列手势特征,根据特征可准确实时的识别数字手势0~9,开发了一个识别率高、实时性好、鲁棒性强的实时识别系统。算法流程如图1所示。
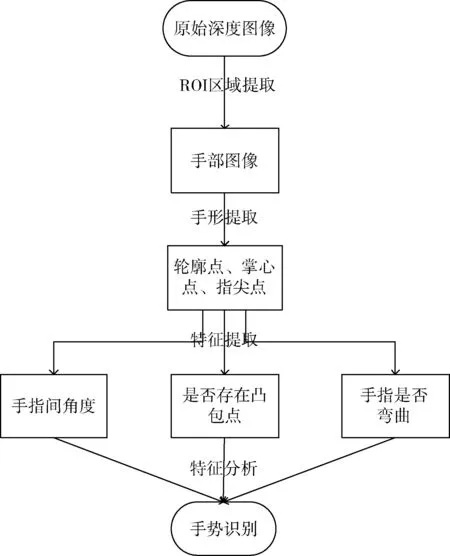
图1 算法流程
1 手部图像分割
1.1 Kinect获取图像
Kinect设备由RGB摄像头、深度传感器、红外线发射器组成,可实时捕获场景中的彩色、深度信息。深度传感器每秒可获得30帧图像,深度图像是场景深度信息的图形化表示,每个像素点的灰度值代表物体距离摄像头的远近,数值越小表示场景距离摄像头的距离越近,反之亦然。图2所示为利用Kinect设备获取的手势信息,也是实验中要识别的数字手势,依次为数字手势0~9。

图2 数字手势
1.2 阈值分割
为了实现数字手势识别功能,需选取一个合适的阈值将手势与背景分割。本文实验采取了一种自适应计算单阈值的简单高效方法——Ostu阈值分割法[10]。
Otsu阈值分割法原理:
假设图像由前景区域和背景区域两部分组成,计算不同阈值下前景区域和背景区域的灰度直方图,当类间的方差达到最大时,对应的阈值就是要求的最佳阈值。对于一幅图像,假设具有N个像素点,图像的灰度总级为L,pi表示灰度级为i的像素点出现的概率。对任意灰度值t(1≤t≤L), 可按照t将图像的灰度级分为两类,C0={1,2,3,…,t},C1={t+1,t+2,…,L},C0所占比例为w0,灰度均值为u0,Ci所占比例为w1,灰度均值为u1,则整幅图像的灰度均值为u=w0*u0+w1*u1, 建立目标函数g(t)=w0*(u0-u)2+w1*(u1-u)2, 该函数是阈值为t时的类间方差表达式,当g(t)取值为最大值时,对应的t为最佳阈值。
实验中,深度图像包括手掌、躯干以及背景部分。为提高分割的精确度要对图像进行多次迭代阈值分割,但多次迭代分割势必会占有大量计算资源,导致识别效率降低。观察图3所示的图像灰度直方图可发现,无论距离Kinect是远是近、无论何种手势,人体躯干部分始终处于灰度直方图的最高峰。找到灰度直方图最高峰点处的灰度值,在最小灰度值Tmin和峰值对应的灰度值区间内进行阈值分割,得到的阈值T即为手掌和躯干的分界点,在提高分割精确度的同时又降低了时间复杂度。
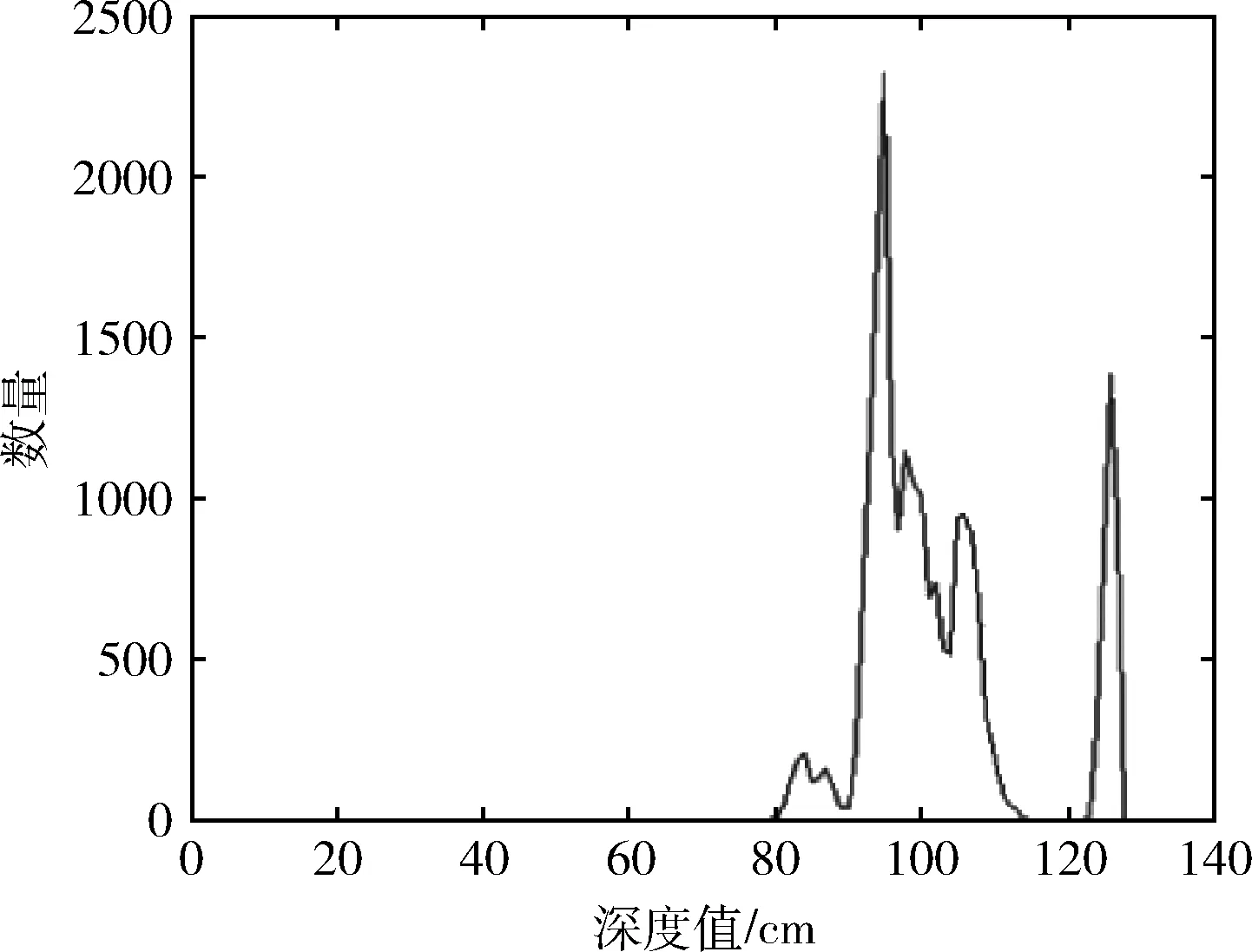
图3 灰度直方图
2 手形提取
手势分割完成后,手部区域从复杂背景中分割出来。为了方便提取特征进行手势识别,需要提取手部区域的轮廓点、掌心点以及指尖点等信息。
2.1 轮廓点提取
在做手势动作时,手部必然是悬空的,不和躯干或者其它物体贴合。结合轮廓点独有的性质,在轮廓点的3*3邻域内,必然有一个方向点的灰度值不在手部区域内,而非轮廓点却不具有这样的性质。利用该性质得到获取手部轮廓点的具体步骤:
步骤1 设手部轮廓点集合mContour,内部点集合mHandArea。依次遍历所有点,对于当前点P,若它不在图像边缘位置,且其灰度值在区间 [Tmin,T] 内,则转向步骤2。整个循环结束后,转向步骤5;
步骤2 判断点P的3*3邻域内像素点的灰度值,是否存在一点的灰度值不在 [Tmin,T] 范围内。若存在这样的点,则转向步骤3,否则,转向步骤4;
步骤3 将点P存入mContour中,返回步骤2;
步骤4 将点P存入mHandArea,返回步骤2;
步骤5 遍历完成后,对图像进行二值化处理。效果如图4所示。
2.2 获取掌心点
考虑到掌心的特殊性,无论何种动作掌心的面积始终大于手指部分面积,因此可以考虑将最大内切圆的圆心作为手掌中心。相对手掌来说,手指本身纤细,手指内部点的内切圆半径要远远小于手掌内部点的内切圆半径,所以此方法可行。
假设掌心点坐标为 (x0,y0), 遍历集合mHandArea中的每个点,计算该点和轮廓点mContour中每个点的距离,记录最小距离值,在所有内部点和轮廓点的距离最小值中找到最大值,此时对应的手掌内部点坐标即为要找的掌心。
2.3 获取指尖点
指尖点是轮廓点里的特殊点。考虑指尖点独有的性质,在其对应的手指轮廓点中,指尖点距离掌心点一定是最远的。为了将手指区域划分,必须先根据掌心点舍去部分轮廓点以及手掌末端的点,保留手指尖端轮廓点。计算所有轮廓点到掌心点距离的均值,一般而言,距离小于该均值的轮廓点要么是手掌部分轮廓点,要么是手掌末端的点,因此将距离小于均值的轮廓点舍弃后即可得到分离的手指点。利用下面的步骤在分离的手指点中找到指尖点。
指尖点判断步骤如下:
步骤1 遍历轮廓点集合mContour,求得掌心点到所有轮廓点的平均距离Daver;
步骤2 遍历轮廓点集合mContour,计算当前点和掌心点的距离,若大于Daver,则将其加入tmpfinger(手指区域轮廓点),若小于则舍弃。循环结束后,转向步骤3;
步骤3 遍历tmpfinger,找到距离掌心点最远的点,将其加入指尖点链表mfinger,然后删除与指尖点距离最近的点,再将被删除的点进行递归迭代删除,直到无法删除为止。若tmpfinger链表中仍有剩余点,则继续执行步骤3,否则转向步骤4;
步骤4 遍历指尖链表mfinger,将指尖点以及附近的点全部归一化为白色,使得指尖点与轮廓点在视觉上有所区分。如图4所示。

图4 手部分割效果
图4所示为手形提取完成后的手部深度图像。可以看到,手部区域、轮廓、指尖点、掌心点都较为清晰、明确。
2.4 轮廓点有序化
上文中得到的轮廓点是无序的,但是特征提取时需要用到有序的轮廓点,因此要对轮廓点进行排序操作。距离最近的两个像素点必是相邻点,因此只要从任意一轮廓点依次寻找距离最近的点,便可以将轮廓点有序排列。
3 特征提取及手势识别
(1)手势0特判
相较于其它手势而言,数字手势0不具备本文手势判别的任何一个特征,因此需要对手势0进行单独判定。利用回归分析法得到式(1),当满足式(1)时,可以认为该手势是拳头。Dk是人与Kinect之间的最短距离,Dmax是轮廓点距离掌心的最大距离,Dmin是最小距离
Dmin2-Dmax2≤C-Dk2
(1)
其中,C为常数,实验时设定值为1130。
(2)手指点个数N
数字手势1~5皆是依据手指点的个数来判断。
(3)凸包检测
找到手势轮廓中最上方包围特征点H和最左侧包围特征点L,扫描包围特征点所包围的轮廓点,若存在轮廓点在包围特征点连线的外侧,则判定存在凸包点,否则判定无凸包点。如图5手势存在凸包点,判定为手势7。
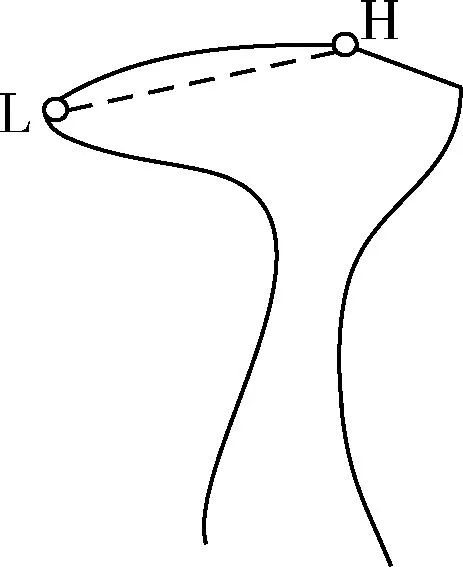
图5 凸包检测
(4)相对距离
手势判定时,手势9和手势1皆被系统判定为只存在一个手指点,唯一区别在于手指是否弯曲。仔细观察发现,若手指无弯曲,手指轮廓中的点和指尖点的相对距离不会大于手指的宽度,若手指弯曲则相反。因此可计算相对距离来判定手指是否弯曲。
距离计算方法如下:
如图6中所示,首先找到指尖点Pf,在对应手指轮廓点中找到距离指尖点一定距离的点记为Ps,计算两个点间的相对距离Dis=|Pf·x-Ps·x|, 设置一个阈值thr,若Dis≥thr,判定手指为弯曲状态,否则判定手指为竖直状态。经过反复实验可得,Ps取距离指尖点30像素处的点,阈值thr设定为10较为合适。
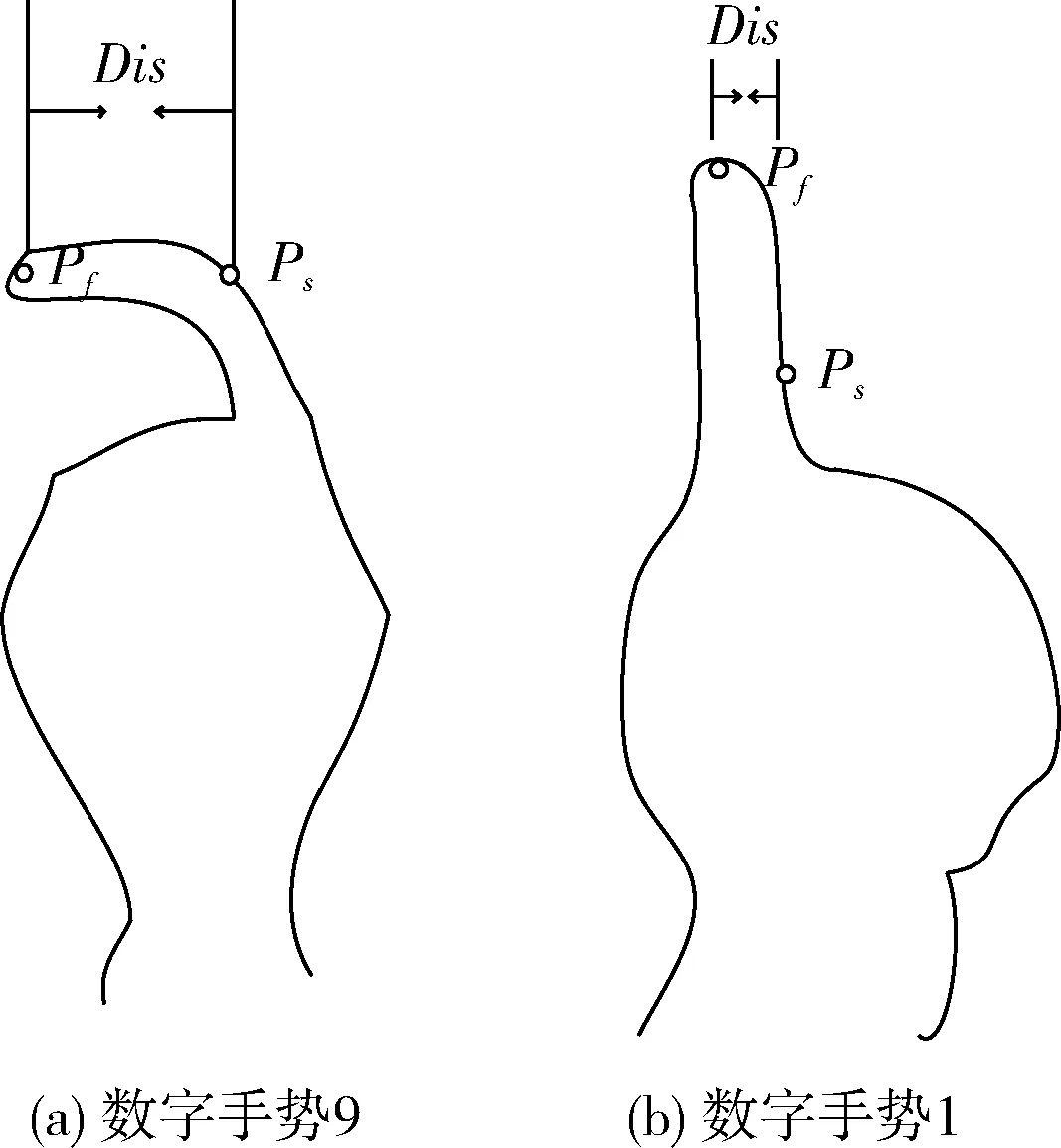
图6 距离
(5)角度特征
通过实际观察测量,常人的五指分开后手指之间的角度在0°~180°之间。角度指的是连接指尖点和掌心形成的向量之间的角度。其中大拇指和食指之间的角度在40°~90°,食指与中指间的角度为10°~35°,大拇指和小拇指之间的角度为100°~150°。
总结以上可得手势识别具体步骤如下:
步骤1 若手指点的个数为0,且符合式(1)则判定为手势0,否则进行凸包点检测,若存在凸包点则判定为手势7;
步骤2 若手指点的个数为1,则计算手势点与特定点之间的相对距离,若距离大于thr,则判定为手势9,否则为手势1;
步骤3 若手指点的个数为2,计算两个指尖点的角度。若角度在10°~35°之间,判定为手势2,若角度在100°~150°之间,判定为手势6,若角度在40°~90°之间,判定为手势8;
步骤4 若手指点个数为3,判定为手势3;
步骤5 若手指点个数为4,判定为手势4;
步骤6 若手指点个数为5,判定为手势5。
4 实验结果及分析
实验时随机邀请了10名志愿者,测试时需面对Kinect设备,使手掌位于身体的最前端,按照图2所示手势做出动作,每个动作重复10次,每个手势共计100次。
由于Kinect本身的物理限制,其测距范围是60 cm~200 cm,因此首先在不同距离下进行了测试。表1展示了3种不同距离下的测试结果。

表1 不同距离下手势识别结果
从表1中可以看出,手势一、二、三、四、五、九的识别率较好,识别率都在97%以上。其它的手势的识别略低,但也均在95%以上,总体符合预期识别效果。可以看出,随着人与Kinect距离的增大,识别率略微下降,这是由于近大远小的规律,距离较远时获得的深度图像尺寸较小,为识别增大了难度。虽然识别率有所降低,但平均识别率依然保持在95%以上。
对比各个手势的识别率,发现数字手势0的识别效率稍低,这是由于数字手势0的特判式(1)中参数C为多次实验后得到的数值。数字手势7识别率低的原因在于识别时将聚集的手指尖端部分误判为手指点,导致识别错误。虽然两种手势的识别率相对于其它手势较低,但也达到了97%。
将本文方法与文献[6]和文献[11]所提出的方法进行对比,结果见表2,表中所示为共有手势的识别率。由表2可以得出,文献[6]的平均识别率为98.8%,文献[6]使用的方法是通过建立六级分类标准识别手势,使用的特征较为复杂,在获取手部轮廓和特征提取过程耗时较多,实时性较差。文献[11]的平均识别率为96.7%,它使用了基于YCbCr颜色空间提取手部的方法,对肤色和光照条件较为敏感,且定义的手势皆为伸直状态,不符合日常生活中人们对手势的定义,降低了实用性。本文方法的平均识别率达到了98.8%,并且克服了以上方法中的缺点,在各种情况下都可以得到正确的识别结果。
为了验证本文方法具有旋转、平移、缩放不变性,分别让测试者在手部旋转、平移及距离设备不同远近下进行测试。结果如图7中所示,图7所示为实验所开发的识别系统界面,界面中展示了人与Kinect之间的最近距离、识别结果,原始深度图像和处理后的手部图像。可以看到在各种情况下,本文实验开发的手势识别系统都可正确识别手势,说明本文使用的方法满足旋转、平移、缩放不变性。

表2 不同方法识别结果对比

图7 旋转、平移、缩放测试
为了验证在光照和肤色变换条件下的鲁棒性,测试者分别在戴手套和不同光照条件下进行测试。但是由于实验本身是基于深度图像的识别,不会受到光照的影响,因此图8只展示了测试者戴手套的测试结果。可以看出在这种情况下也可正确识别手势。

图8 戴手套测试
实时性方面,将本文所用方法与文献[6]所用方法各步骤处理时间做了简单对比。从表3中可以看出,本文所用方法各步骤耗时较少,识别速度快,实时性较高。
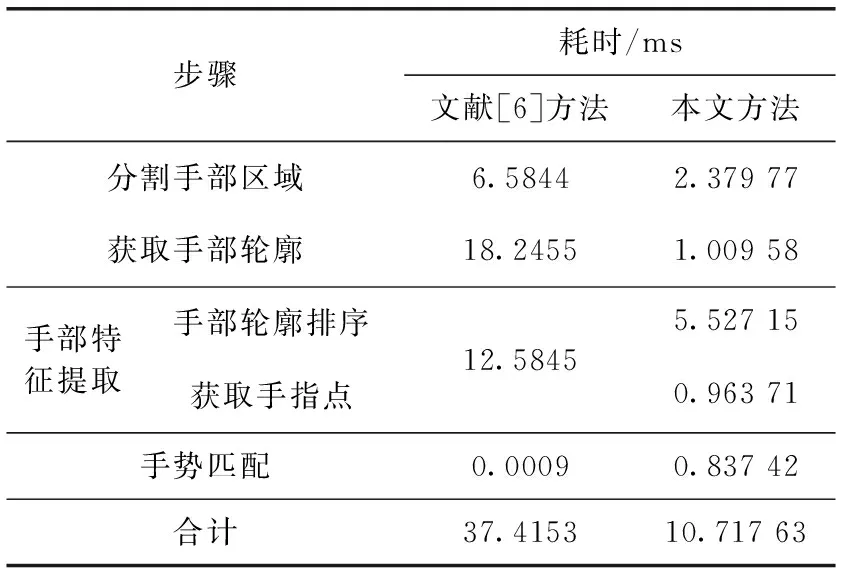
表3 各个步骤处理时间
5 结束语
本文提出一种基于Kinect的实时手势识别算法,该算法可准确识别数字手势0~9。首先利用阈值分割法将手部图像分割出来,然后提取一系列手形特征,掌心、轮廓点、指尖点等,根据得到的手形特征提取手势特征,指间的角度、是否存在凸包点、手指是否弯曲等,最终根据手势特征实现数字手势的判定。本文提出的方法可满足手势的旋转、平移、缩放不变性,具有较高的计算效率,且具有良好的实时性与稳定性。接下来的工作就是进一步完善系统,并将之推广应用到其它领域,如智能家庭、虚拟游戏当中。

