加权聚合图像引导滤波
陈 彬,谭新成
(1.武汉科技大学 信息科学与工程学院,湖北 武汉 430081;2.武汉科技大学 机器人与智能系统研究院,湖北 武汉 430081)
0 引 言
边缘保持滤波是图像处理及计算机视觉领域一个最为基础的处理方法,其在众多应用中(如:高动态图像[1,2]、图像增强[3,4]、图像去雾[5,6]以及双目立体匹配[7,8]等)发挥着重要作用。总结起来,边缘保持滤波算法可分为两大类:全局正则化优化算法和局部算法。其中,全局正则化优化算法(如:L0范数梯度最小化(L0)[9]、全变分(TV)[10]以及加权最小二乘(WLS)[11]等)是通过在整幅图像范围内优化一个指定的代价函数来实现保边滤波的目的。相应地,局部算法(如:双边滤波(BF)[12,13]、递归图像滤波(RIF)[14]和引导滤波(GIF)[3,4,15])则是在一个较小的局部区域内对滤波输出进行计算和估计。一般而言,全局算法相较于局部算法具有更好的质量,而局部算法则具有更小的算法复杂度。引导滤波(GIF)是一种基于线性回归模型的边缘保持滤波算法。相较于双边滤波,引导滤波具有更低算法复杂度(O(N))的同时依旧能取得与双边滤波相当的效果。作为一种局部滤波算法,引导滤波依旧具有局部算法普遍存在的不足,即在平滑图像的同时可能会使一些较弱的图像边缘在最终输出图像中变得模糊,如此将可能在输出图像中引入光晕效应(halo artifacts)。本文从引导滤波的原理出发,着重分析了引导滤波的聚合策略,提出了一种加权聚合方法。实验结果表明,利用该加权聚合方法,引导滤波在平滑图像的同时将能获得更为尖锐的边缘,极大地抑制了滤波输出图像中的光晕效应。
1 引导滤波
在介绍本文所提出的加权聚合引导滤波之前,本小节先简要介绍、分析一下引导滤波及其已有代表性改进算法。
所谓引导滤波,即在一幅图像的引导下对输入图像进行滤波处理。引导滤波首先假设在一个很小的、以像素k为中心的局部窗口wk内,滤波输出图像Q与引导图像I呈一种线性变换关系,该线性关系可由下式表示
Qk(i)=akI(i)+bk, ∀i∈wk
(1)
其中,ak,bk为窗口wk内的两个线性系数。而后,引导滤波定义了一个代价函数E(ak,bk) 用以衡量式(1)的输出与待滤波图像P之间的差异,该代价函数如下所示
(2)


(3)


随着滤波窗口wk的滑动,待滤波图像中的某一个像素点i将会包含在多个滤波窗口内,则该像素点在每个包含该像素的窗口内都将得到一个滤波结果(式(1)~式(3)),引导滤波算法(包括WGIF和GDGIF)将这些结果的均值作为该像素点的最终输出Q(i)
(4)
式(4)所示的过程,本文将其称为均值聚合策略,其具体计算过程请参考文献[3,4],在此不再赘述。
2 加权聚合引导滤波
2.1 加权聚合

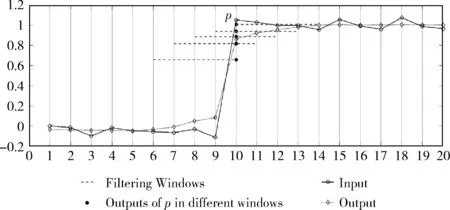
图1 一维加噪阶跃信号处理
基于上文的分析,本文将引导滤波的均值聚合(见式(4))修改为如下式所示的加权聚合方式

(5)

(6)
式(6)所示的MSE表示在窗口wk内滤波输出与输入的差异程度。很明显,ek越小表示在窗口wk内的计算结果更为接近输入值,即该窗口的计算过程其置信度更高,那么该窗口分配的聚合权值应该较大。相反地,若ek越大,窗口wk的聚合权值应该越小。据此分析,本文将窗口wk的聚合权值βk与其MSE(ek)之间的函数关系定义为
(7)
其中,η>0是一个较小的常数。
为了直观地说明本文所描述的加权聚合策略的效果,这里依旧以一维加噪阶跃信号作为输入,并将本文提出的算法结果与GIF滤波器计算得到的结果进行了比较。图2所示的例子,其输入信号是一个一维阶跃信号,并在此基础上叠加了一个均值为0,方差为0.002的高斯白噪声,用以模拟图像的纹理信息。图2(a)与图2(b)分别展示了在取不同参数的情况下,两种算法结果的对比。通过本示例可以明显看出,加权聚合(η=0.002)方法相较于原始的均值聚合方法能更好地保留信号的边缘信息。需要指出的是,在选取较大的平滑参数情况下(如图2(b)所示),本文的算法在很好地平滑信号的噪声(纹理信息)同时,依旧能完整保留了信号的边缘信息。与此同时,GIF则明显地模糊了信号的边缘,即可能在输出信号中引入了光晕效应。

图2 一维信号处理结果
2.2 算法描述
将式(3)所示的bk计算公式代入式(6)中,则窗口wk内的MSE(ek)可表示为

(8)

(9)
依据式(8)和式(9),加权聚合引导滤波算法的具体过程可由算法1加以表示:
算法1: 加权聚合引导滤波
输入: 待滤波图像P, 引导图像I,

输出: 滤波输出图像Q
(1)M=2*r+1;



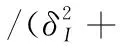
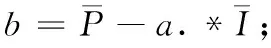
β=exp(-e./η);
sumβ=mean(β)*M;
(5)betaa=(β.*a)./sumβ;
betab=(β.*b)./sumβ;
(6)Q=(mean(betaa).*I+mean(betab))*M;
其中,.*和./分别表示两个矩阵间对应元素相乘和相除,而mean则代表半径为r的均值滤波操作。如文献[3,4]所述,若采用盒滤波(box filter)技术,均值滤波mean的算法复杂度与输入图像的像素个数N呈线性关系,如此算法1所示的加权聚合引导滤波算法的算法复杂度也将仅与输入图像的像素个数呈线性关系,即为O(N)。
3 实验结果
在展示和分析了一维信号处理结果的基础上,本小节将展示和分析本文算法对图像的滤波结果,并将结果与其它流行的边缘保持滤波算法(GIF和BF)进行比较。图3展示了本文算法在不同参数情况下对一幅灰度图像进行处理后的结果,其中参数η设置为一个常数0.002。

图3 灰度图滤波结果


图4 本文算法与GIF、BF的对比


图5 彩色图像滤波结果
4 结束语
本文在对引导滤波的基本原理进行了系统、详细的分析基础上,从引导滤波的聚合策略入手,将其均值聚合方法改进为加权聚合策略,进而提出了一种加权聚合引导滤波算法。相较于引导滤波或双边滤波等流行的图像边缘保持滤波算法,本文提出的算法不仅能有效地平滑图像的纹理信息,同时又能更好地保留图像的边缘信息,此外,值得特别指出的是,本文算法的算法复杂度是线性的,与引导滤波一样为O(N)。 鉴于加权聚合引导滤波算法的特点,除了图像滤波,它还能应用于图像增强,高动态图像压缩、图像去雾以及双目立体匹配领域,具有广泛的应用前景。

