基于相位检测的双平面摄像机标定

陈文艺，来庆盈，杨 辉

(1.西安邮电大学 物联网与两化融合研究院，陕西 西安 710061；2.西安邮电大学 通信与信息工程学院，陕西 西安 710121)

0 引 言

计算机视觉最基本的工作就是根据物体的几何信息对空间中的物体进行重建从而恢复出物体的形貌，在立体空间中物体表面的某一个物理点在该空间中所处的位置与二维图像中的某一像素点坐标是相互对应的，这二者间的关系是根据摄像机模型来最终确定的。该模型中所包含的物理参数就是标定中通过一系列实验与推导计算得出的摄像机内外参数[1]，对这些物理参数进行推导的过程称为摄像机标定[2]。

摄像机是视觉系统中的重要组成部分同时也是计算机视觉获取二维图像最主要的工具。摄像机标定技术作为视觉系统中不可或缺的一项技术，其在三维重建、人工智能以及机器视觉等各个领域都有广泛的应用前景[3,4]。到目前为止，涌现出了大量经典的标定方法[5]，同时也衍生出了许多摄像机标定的新技术[6]。其中双平面标定法在标定中占据了重要的地位，文献[7]在双平面标定方法的基础之上确立了较为完善的标定模型，同时通过非线性优化的方式得到相应的参数，该方法降低了累积误差对于最终标定精度的影响；文献[8]在双平面模型中采用最小二乘法对摄像机参数以及畸变系数进行预估，并将其应用到了钢板的长度、宽度以及厚度的尺寸测量中，该方法现场标定的工作量较小；文献[9]将双平面法引入到了多个摄像机的标定工作中，该方法操作比较容易并且标定成本较低，但是标定的计算量过大。

本文通过对摄像机模型标定理论的研究，根据标定模板与成像面的相位对应关系确定物点、像点间的一一对应关系，并且在双平面摄像机模型基础上建立了虚拟摄像机模型，在该模型中实现了标定图像的畸变校正。

1 工作原理

双平面摄像机模型通过获取两个标定平面的标定点坐标以及投影光线与平面的相交关系完成摄像机标定。为更好的对标定结果进行验证，在该模型基础上建立虚拟摄像机模型。

1.1 虚拟摄像机模型

该模型在双平面摄像机模型基础上引入虚拟成像平面C，其模型如图1所示。

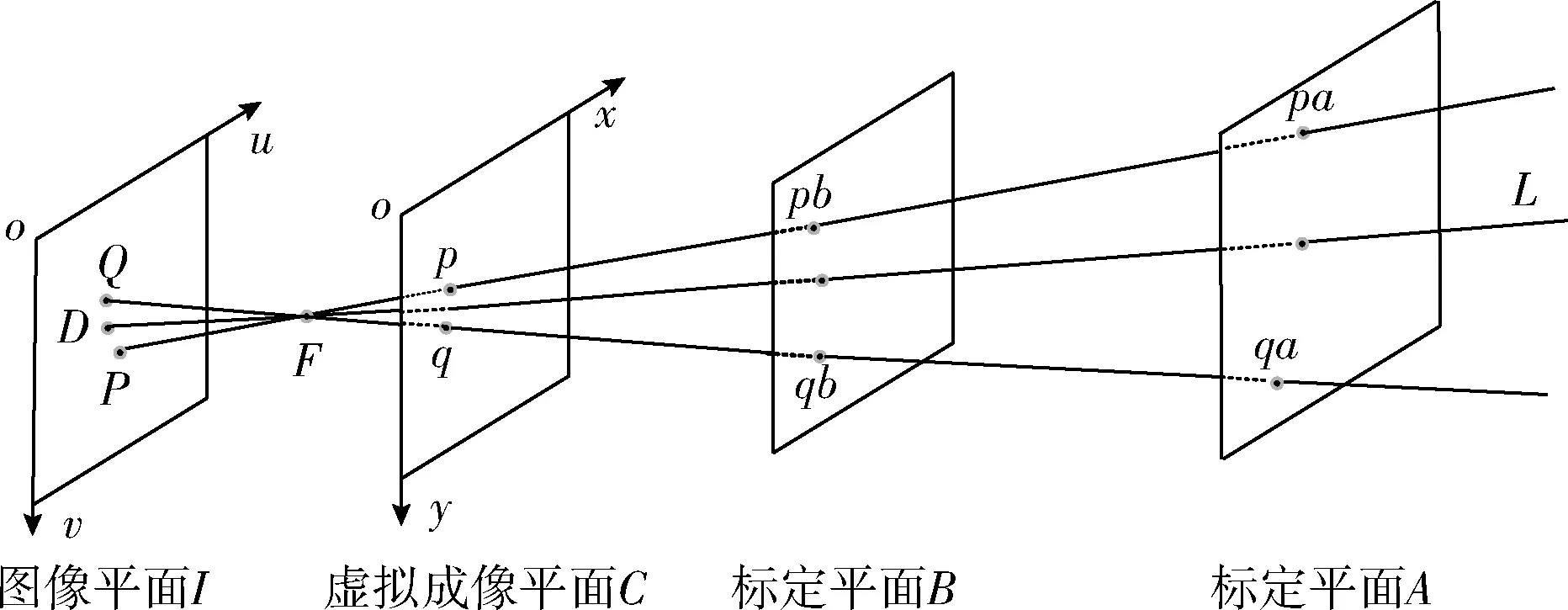
图1 虚拟摄像机模型

该模型中包含光心、虚拟成像平面、虚拟主点和虚拟光轴。如图1所示，将光心定义为图像平面I中所有像点所对应的空间直线汇聚的交点F，虚拟光轴定义为垂直于两个标定平面的空间直线L；虚拟成像平面则定义为垂直于虚拟光轴且与图像平面I等焦距的对应平面C；虚拟主点则定义为虚拟光轴和虚拟成像面C间的交点d。

1.2 摄像机标定原理

如图1所示，结合两标定平面的相位分布得到物点与像点间的映射关系，并根据均方误差和最小原理确定光心坐标。在此基础上，建立虚拟摄像机模型，从而建立传感器像平面I(u,v) 和虚拟像平面C(x,y) 间的坐标映射关系，从而得到式(1)所示的函数表达式，实现标定图像的畸变校正

(1)

其标定的基本思想如图2所示。首先采集两幅不同位置处的实心圆点标定板图像并进行灰度化处理，对其进行条纹分离后检测横竖条纹的相位分布，通过相位不变点对应同名点的原理对虚拟光轴对应像点坐标进行标定；然后采用最小二乘拟合法对该点位置处的横竖条纹相位分布进行修正，从而获取条纹图像的理想载波角频率，并根据理想载波角频率得到条纹图像的真实相位，利用标定模板和成像面图像的相位对应关系建立物点和像点间的对应关系，进而实现光心位置的标定；最后，通过物点、像点之间的对应关系以及光心坐标确定传感器成像面与虚拟成像面的坐标映射关系，结合灰度级插值算法对原图像的畸变进行校正。

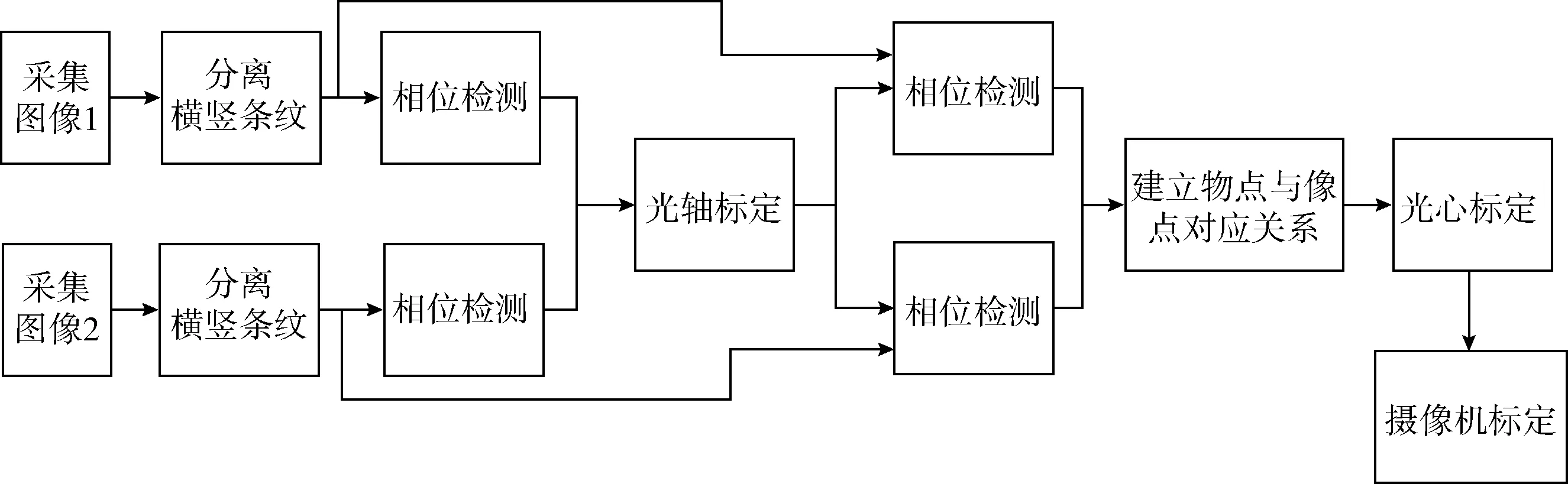
图2 摄像机标定基本思想

在实际摄像机标定中，镜头畸变、靶面安装误差都会使图像发生畸变，即虚拟成像面的图像与实际成像面图像不是过光心的直线对应关系，因此通过建立各种摄像机畸变模型可以描述摄像机畸变，并通过标定估计畸变模型参数。本文采用隐式的畸变标定方法，不明确使用摄像机畸变模型，通过逐点获取虚拟成像面C的图像与实际成像面I图像位置的映射函数，实现畸变校正。

1.3 采集标定板图像

在进行实际标定实验时，由于圆点标定板固定在标定平台上不方便移动，因此利用步进电机移动摄像机对标定板进行拍照，利用光栅尺记录摄像机的移动距离，其效果等效于双平面的摄像机标定。实验所采用摄像机为工业检测摄像机，分辨率为960pixel×1280pixel，所采用的标定板为实心圆点标准标定板，其圆点直径为4 mm,圆心距为8 mm。在不同位置采集的标定板图像如图3所示。

图3 标定板采集图像

图3中图(a)为A位置处的标定板采集图像，图(b)为B位置处的标定板采集图像，两处位置距离150.015 mm。

2 标定图像相位检测

2.1 滤波分离横竖条纹

本文采用高斯频域滤波的方式对标定图像进行条纹分离。由于标定图像的边缘包含很多无效的信息，为了得到较好的条纹图像，首先需要对实心圆点标定图像进行圆点外插；然后对外插图像进行二维傅里叶变换得到其频域图像；再采用高斯滤波器在频域从x和y两个方向对频域图像进行相应的滤波处理；最后将改变后的频域图像进行二维傅里叶反变换，获取标定图像滤波后在x、y两方向上的条纹图像。

以标定平面A为例，频域高斯滤波后得到x、y方向的条纹图像如图4所示。

图4 标定平面A条纹图像

2.2 条纹相位检测

平面标定板上x、y方向的理想条纹光强分布可以表示为

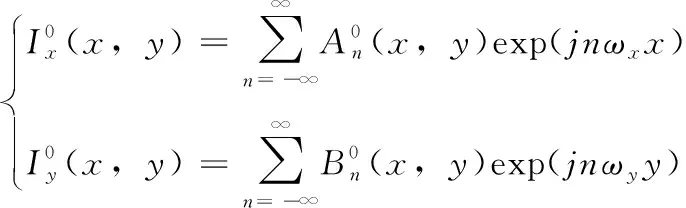
(2)

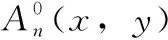
由于摄像机存在畸变，畸变效应会对标定板条纹图像的相位进行调制，采集得到的标定图像在x、y方向的条纹图像光强分布可以表示为

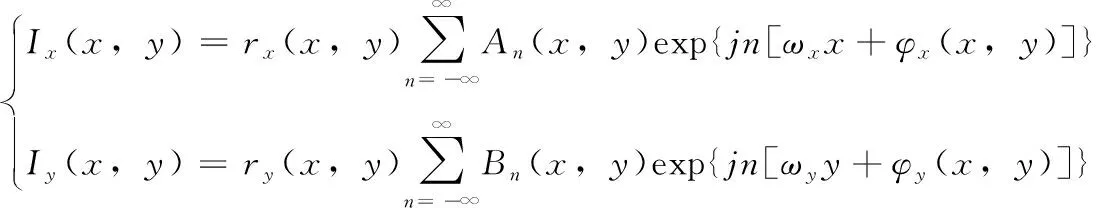
(3)

其中，rx(x,y)、ry(x,y) 分别代表标定板表面的非均匀反射率，An(x,y)、Bn(x,y) 表示经过相位调制后的傅里叶系数，φx(x,y)、φy(x,y) 为带有摄像机畸变的条纹图像的相位分布。采用正交相干解调法能够直观获取条纹的相位分布,虽然标定板条纹图像的相位分布是二维的，但是能够以一维方式逐行逐列的获取条纹的相位。以x方向条纹图像为例，将条纹图像的某一行I(x,yc) 分别乘以载波sin(ωcx) 和cos(ωcx), 并通过低通滤波后将除±(ωx-ωc) 以外的频率分量去除，可得

(4)

其中，ωc为带有摄像机畸变的条纹图像的载波角频率。当ωx=ωc时，便能够获取条纹任意一行的相位分布，理想条纹的载波角频率可采用最小二乘拟合法得出，由此可逐行解调出标定板的x方向条纹相位分布φx(x,y), 同理也可逐列解调出y方向相位分布φy(x,y)。

根据理想载波角频率检测标定平面横竖条纹的相位分布，由于边缘条纹图像存在边缘效应，对于整体标定精度的影响比较大，因此去除横竖条纹边缘的部分条纹。以标定平面A为例，对其横竖条纹进行相位检测，由于噪声等影响，其相位分布起伏比较大，因此对测量结果进行多项式拟合。其中对竖条纹进行逐行解调和相位去包裹，多项式拟合后获取标定平面A的竖条纹相位分布如图5(a)所示；同理对横条纹进行逐列解调和相位去包裹，多项式拟合后获取横条纹的相位分布如图5(b)所示。

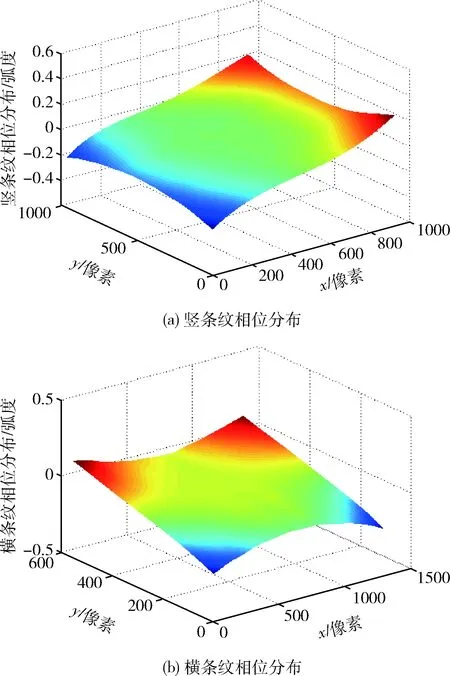
图5 标定平面A条纹相位分布

3 双平面摄像机标定

3.1 虚拟光轴标定

根据摄像机的成像特性可知，当摄像机到物体间的距离发生改变时，在传感器成像面上的图像也会随之产生一定程度的缩放。若主光轴没有发生改变，则光轴和二维平面间的交点位置将保持恒定，即该交点位置处的相位值保持不变。因此双平面摄像机模型中标定平面中图像相位不变点所对应的同名点就是虚拟光轴和像平面间的交点，根据该点在标定平面A、B上的对应点坐标可确定该模型下的虚拟光轴。若标定平面A的条纹载波角频率为ωAx, 标定平面B的条纹载波角频率为ωBx, 则设ωCx=(ωAx+ωBx)/2, 根据正交相干解调法得到标定平面A和标定平面B的相位分布为

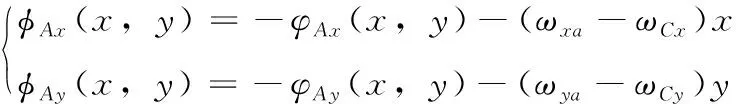
(5)

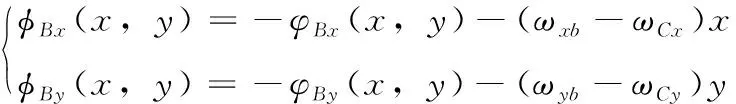
(6)

根据式(5)和式(6)可得，两幅标定图像在x、y方向上的相位差为

(7)

对相位差分布进行去包裹，根据相位展开的原理可知，由于解包裹的影响，其真实的相位差分布与解包裹得到的相位差分布之间相差2πk(k为整数)。因此将解包裹得到的相位差分布±2πk， 使相位差分布的中心区域调整到k=0的部分。截取横竖条纹中心区域相位差为0附近的一定区域的曲面分别进行插值拟合，得到相位差为0的点即为虚拟光轴与图像平面的交点。根据实验数据可得该点像素坐标为(525.552,606.602)。

3.2 建立像点与物点的对应关系

为了确定任意像点和物点的对应关系，需要在标定平面横竖条纹相位分布的基础上加入一级谐波相位。对于成像面上任意一点P(u1,v1) 在标定平面B和标定平面A上分别对应pb(X2,Y2,Z2) 和pa(X1,Y1,Z1)， 由标定模板与成像面间的相位分布间的相互对应关系可知,两个标定模板与其对应的成像面上的标定图像在x、y方向上的谐波相位对应关系可表示为

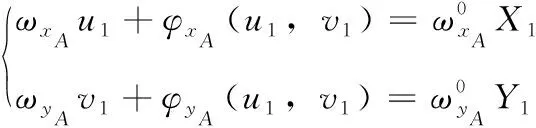
(8)

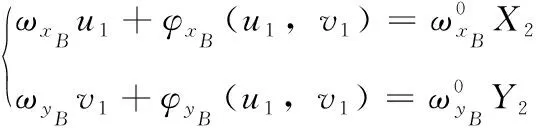
(9)

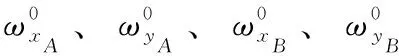
已知标定板的周期Px=Py=8mm, 根据式(8)和式(9)可得到像平面上每一个像素点在标定模板A、B上所对应的X、Y方向上的世界坐标。两标定模板的位置已知，由此可以根据世界坐标系原点位置确定两标定模板Z方向的世界坐标。从而计算出任意像点在世界坐标系中所对应的物点坐标，确定任意像点所对应的空间直线，从而建立三维物点和二维像点间的映射关系。其部分空间直线集如图6所示。

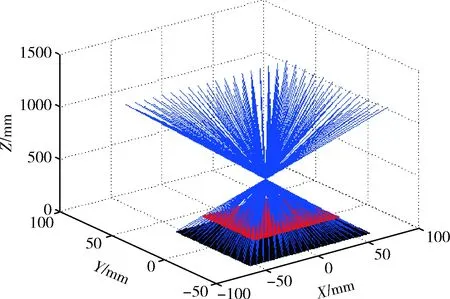
图6 部分空间直线集

3.3 标定光心位置坐标

由于两个标定平面相互平行，摄像机的主光轴垂直于两个标定平面并且经过光心，因此光心的横纵坐标可由虚拟光轴来确定。将虚拟光轴和标定平面A的交点作为坐标系原点，标定平面A的x、y方向分别为X、Y轴，并将虚拟光轴作为Z轴建立统一的世界坐标系。在理想状态下，两个标定平面所对应的空间视线集汇聚于一点，该点即为光心。但实际上，由于畸变等因素的影响，空间视线集会在光心附近形成无数个交点。因此需要在一定范围内遍历Z轴，得到每一个Z值所对应的z平面上所有空间直线与z平面的交点，计算所有交点到虚拟光轴与z平面交点间的距离和，根据最小距离和的原则对光心位置进行估计，使其所对应的均方误差和最小。

图像坐标系中任一像点所对应的两标定平面空间直线可表示为

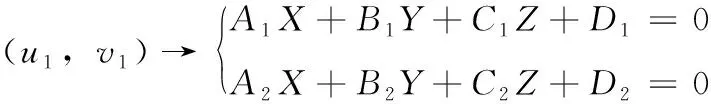
(10)

其式中的未知参数均可由两个标定平面的世界坐标求出。根据虚拟光轴可以确定光心在X、Y方向的世界坐标(X,Y)。对于图像坐标系中N个像点可得到N个空间直线方程组，给定任意一Z值，根据空间直线方程可以在z平面上得到N个交点坐标 (Xi,Yi), 该点与Z值所对应的光心间的距离可由式(11)得出

(11)

di也代表了该交点与Z值所对应的光心坐标的误差，因此，将均方误差和最小所对应的Z值作为光心Z坐标的估计。其表达式可表示为

(12)

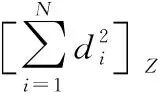
图7 均方误差和分布

由此可得光心在以虚拟光轴与标定平面A交点为原点的世界坐标系中的位置坐标为(0,0,507.496)。

3.4 图像畸变校正

根据光心位置坐标和物点与像点之间的对应关系，能够建立传感器成像面I和虚拟成像面C之间的坐标对应关系。由于虚拟成像面上的图像是没有畸变，由此可实现图像的畸变校正。为降低系统误差，在原虚拟摄像机模型的标定平面A、B的中间位置处定义平面D。以Y方向为例，对于任意像点P，首先根据标定平面A、B所对应的空间直线得到平面D的世界坐标；然后由光心坐标与平面D对应的世界坐标构成空间直线集，根据空间直线集得到虚拟成像面C的世界坐标。将虚拟成像面C的世界坐标转化为像素坐标 (x,y)， 从而得到传感器成像面图像f(u,v) 和虚拟成像面图像f(x,y) 的前向映射关系，由于f(x,y) 的坐标为非整数，其对应坐标的灰度值由f(u,v)的多个像素灰度值来决定，可能造成f(x,y) 像素的丢失，因此需要将前向映射关系转换为后向映射关系生成后向映射表，后向映射表的生成原理可参照文献[10]，从而可以逐像素的生成输出图像f(x,y)， 实现原图像的畸变校正。由此可得标定平面A、B的校正图像如图8所示。

图8 畸变校正图像

4 标定误差分析

为了测量摄像机标定精度，可以利用光心位置坐标和传感器成像面与虚拟成像面的映射关系恢复出两个标定平面的图像，计算其图像的实心圆点质心坐标并将其转化为物理坐标，与标定板实心圆点的实际位置坐标作比较，分析系统标定误差。

对于标定平面A，首先根据生成的后向映射表采用双线性插值算法得到畸变校正后的虚拟像平面图像，检测虚拟像平面圆点图像的质心坐标 (ui,vi) 并根据式(13)将其转换为物理坐标 (x′i,y′i)； 然后根据式(14)利用虚拟像平面与标定平面A间的位置关系得到标定平面A实心圆点质心所对应的物理坐标 (x″i,y″i)， 将其与标定平面A实心圆点质心对应的真实位置坐标 (x,y) 对比；最后根据式(15)、式(16)求其绝对平均误差Δr以及均方误差Δm，可得到标定平面A的标定误差，同理也可得出标定平面B的标定误差

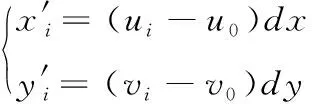
(13)

(14)

式中：f为虚拟像平面到光心的距离，d为标定平面与光心间的距离，dx、dy可由摄像机参数得到

(15)

(16)

由此可得到标定误差对比结果见表1。

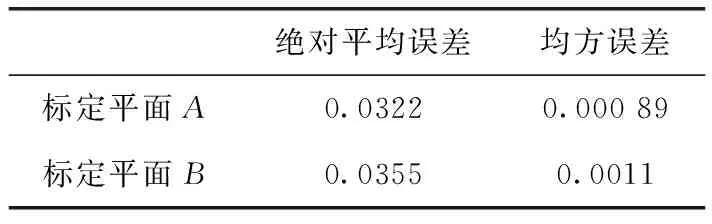
表1 标定误差/mm

由表1可知，两标定平面的绝对平均误差均在 0.05 mm 以内，可以达到比较高的标定精度，验证了该方法的有效性。

5 结束语

本文研究了一种双平面摄像机标定方法，该方法不要求像平面与测量平面平行，并且整个标定过程只需要两幅标定图像即可完成，现场标定工作量比较小；利用标定模板和成像面之间的相位对应关系，不需要繁琐的特征点提取即可确定像点与物点之间的对应关系，同时不必知道任何关于畸变类型的先验知识，在不明确摄像机的物理参数的情况下就能较为精准完成标定工作；以线性的方法完成标定，避免了复杂的物理参数的求解，实验结果表明，该方法的标定精度较高。

本文为降低边缘效应，在标定的过程中去除了部分边缘的条纹图像，因此在后期的研究中可以考虑以线性插值的方式对边缘条纹进行处理，从而进一步对该标定方法进行完善。