层次分析法在高校学生党员发展量化考核中存在的问题

崔释匀

（上海电力大学 电子与信息工程学院，上海 200090）

高校学生党员发展是高校党建工作的重要组成部分，大学生党员是构建中国特色社会主义的后备保障［1］。在当前高校学生党员发展状况下，党员发展量化考核是必然趋势，而高校学生党员发展需要科学的评价体系和考核标准。层次分析法在处理复杂的决策问题上具有实用性和有效性，它是将与决策总量有关的元素分解成目标层、准则层、方案层，在此基础之上进行定量分析的决策方法［2］。

一、层次分析法应用于党员发展量化考核的基本步骤

层次分析法合理地将定性与定量决策结合起来，按照思维、判断的规律把决策过程层次化、数量化。

（一）确定评价指标体系和层次结构

层次分析法中考核指标体系的建立是评价高校学生入党积极分子的前提和基础［3］。本文根据党章，结合高校党建工作者、学生工作专家、辅导员及学生党员等群体意见，确定了两大考核方向，即基本素质（Q1）和能力素质（Q2），包含思想政治、综合学习能力、群众基础、行为规范、实践创新、学生工作6 个评价指标，涵盖22 个二级指标和26个评定指标的评价体系，简称“思综群、行实学”量化评价体系（见表1）。

（二）构造判断矩阵和确定指标权重

判断矩阵是进行层次分析的数据来源，构建判断矩阵是层次分析法的关键［4］。本文采用九级标度法确定两两判断矩阵，设共有n 个元素参与比较，建立判断矩阵A=(aij)n×n，设现在要比较的因素{思想政治、综合学习能力、群众基础、行为规范、实践创新、学生工作}为X={x1x2x3x4x5x6}，结合工作实际，对高校党务工作者、专家学者、学生党员等群体的访谈结果进行整理，按照相关目标的重要程度，得到如下判断矩阵。

基本素质（Q1）方向：

能力素质（Q2）方向：

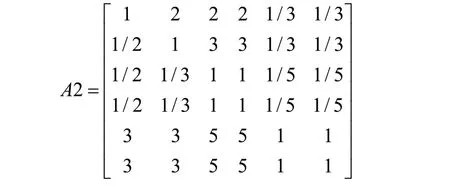
根据判断矩阵，求出其最大特征根λmax对应的特征向量W。方程如下：

所求特征向量W 经归一化，即为各评价因素的重要性排序，也就是权重分配。令W={w1w2w3w4w5w6}，基本素质（Q1）方向，计算得w1=0.300 1， w2=0.147 2，w3=0.189 1，w4=0.212 2，w5=0.075 7， w6=0.075 7；能力素质（Q2）方向，计算得w1=0.127 8， w2=0.116 1，w3=0.056 6，w4=0.056 6，w5=0.321 5， w6=0.321 5。

（三）一致性检验

以上得到的权重分配是否合理，还需要对判断

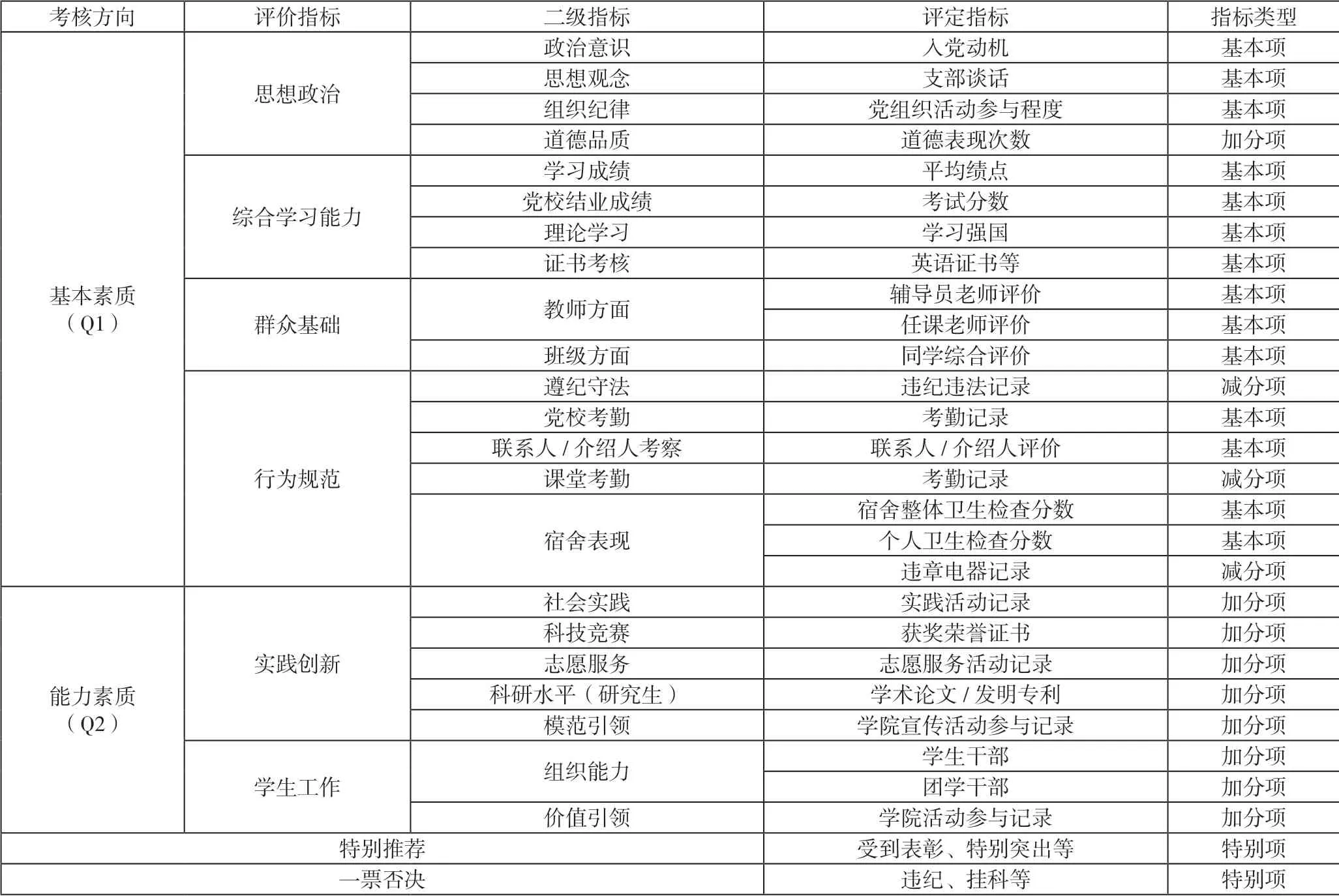
表1 “思综群、行实学”评价体系量化指标

矩阵进行一致性检验。检验使用公式：

式中，CR 为判断矩阵的随机一致性比率；RI 为判断矩阵的平均随机一致性指标，六阶的判断矩阵的 RI 值查表可得RI=1.26；CI 为判断矩阵的一致性指标，它由下式给出：

当判断矩阵A 的CR ＜0.1，或λmax=n，CI=0 时，认为A 具有满意的一致性，否则需调整A 中的元素以使其具有满意的一致性。

基本素质一致性检验：λmax=6.099 1，CR=0.015 7， CI=0.019 8。

能力素质一致性检验：λmax=6.138 2，CR=0.0219， CI=0.027 6。

经层次总排序检验，总排序一致性CR 均小于0.1，满足一致性要求（确定发展对象CR=0.018 8、基本素质CR=0.002 1、能力素质CR=0.020 9）。

（四）计算权重，选择决策

根据设计出的党员发展量化考核指标，构建出层次分析法结构（见图1），经软件计算可以得出底层权重（见表2）。

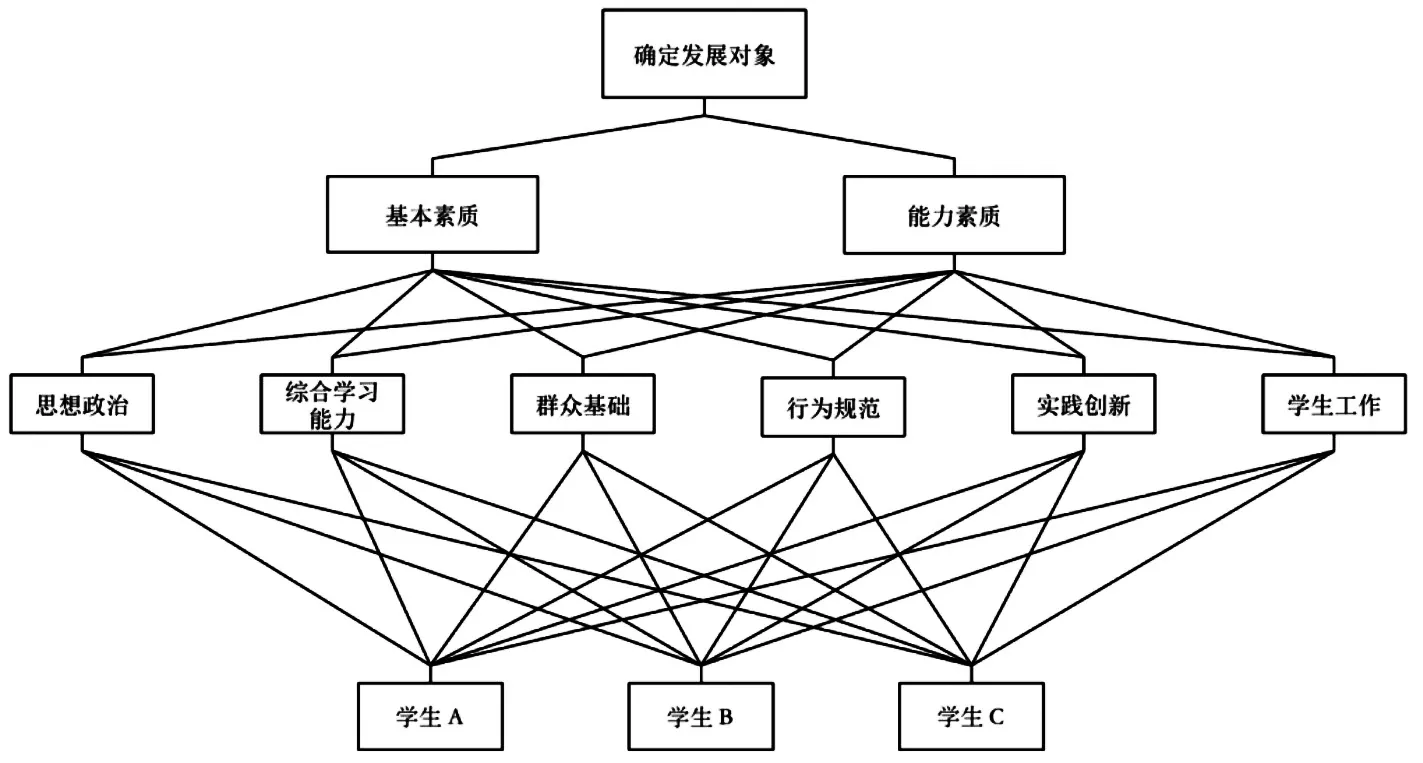
图1 层次分析法结构图

表2 群决策底层结论（权重）表

根据底层权重很明显可知学生A 权重最大，学生C 权重最小，与预期结果相同。

二、层次分析法存在的不足及原因

一是构造判断矩阵不够准确。层次分析法中的比较、判断以及结果的计算过程都是粗糙的，不适用于精度较高的问题［5］。层次分析法是定性和定量相结合的方法，在设置指标体系时，不能满足所有人的需要，必须有所取舍，如欲最大程度地接近具体事实，只能增加不同的各级指标，这样势必增加数据获取和确定权重的难度，使层次分析法的实用性和简捷性不复存在。由此，可以结合相关经验数据和专家群，选取相对重要的指标，确保得出的指标体系有最大可能的代表性。

二是判断矩阵的一致性问题。判断矩阵的一致性问题是层次分析法的核心问题，是获得合理决策的前提条件［6］。判断矩阵的一致性改进，关键问题是有没有考虑最大程度保持决策者的原始判断信息，只获得数学意义上的一致性，没有过多考虑决策者的原始判断，可能会误导决策者。

三是标度的合理性问题。判断矩阵的一致性，很大程度上取决于指标因素的复杂性及构权人员的一致判断能力，而判断矩阵的合理性还受到标度的合理性的影响，包括标度方法、标度值形式与大小［7］。实践中发现，九标度理论中各重要性级别之间的实际差异似乎并没有标度数值本身之间所揭示的那么大，在确定判断矩阵的时候，这种数量上的差异与人们感觉上的差异相去太远，归一化之后有所缓解。

四是判断矩阵的灵敏度问题。判断矩阵的灵敏度分析一般从判断矩阵受扰动和判断矩阵元素的可变范围两个方面讨论。在进行决策时，往往得到的判断矩阵是受到一定扰动而形成的一致的判断矩阵。如果判断矩阵元素在一定范围外变动，但排序依然不变，则能使决策者具有更加确信的方案进行排序。对判断矩阵的灵敏度和一致性结合分析，能够较好地改善灵敏度，同时保持判断矩阵的一致性［8］。

五是层次分析法权重计算问题。层次分析法的权重计算除了特征根法，还有几何平均法、算术平均法、最小二乘法、LAM 法（最小夹角余弦法）等，不同的计算方法，结果会有所偏差，综合运用多种方法计算权重更加可靠。

六是增加评价指标复杂程度也相应增加的问题。随着各层因素增加，判断矩阵的规模会比较大，判断矩阵的一致性更加难以保证，权重矩阵的复杂程度相应也会增加。层次分析法衍生出的很多方法都可以较容易地构造出质量较好的判断矩阵［9-11］。

三、层次分析法应用于高校学生党员发展量化考核的注意事项

（一）党员发展量化考核指标

第一，在党员发展量化中，评价指标上的表现可能会随着大环境变化，层次分析法的指标权重应能够客观地进行调整和修正。第二，在党员发展量化中，依据层次分析法结果进行决策时，应该有合适的指标离散度，以提升定量评价的客观性、准确性和教育性。第三，在党员发展量化中，评价指标应能够充分发挥结果导向的作用，层次分析法的指标权重应能够根据结果导向相应提升。

（二）对层次分析法的再认识

第一，层次分析法是对定性问题进行定量分析的一种多准则决策方法，针对学生党员发展考评体系的构建是一种行之有效的方法。第二，运用层次分析法构建高校学生党员发展量化考核指标时应注意以下几个原则：全面性与独立性原则、科学性与实用性原则、定量与定性评价相结合原则。第三，不同地方高校的层次和状况相差较大，各校应根据自身特点进行相应的因素调整和模型改进。

（三）研究启示

第一，建立健全大学生党员发展质量保障体系，从标准、程序、制度、监督、载体、队伍等层面建设大学生党员发展质量保障系统，是探索高校党员发展工作的有益尝试。第二，提出“核心群”概念，即在大学生综合素质能力评价时，相对优秀的学生比较固定，这些是在各个方面都比较优秀的学生组成的群体。“核心群”的成员是党员发展的主力军，利用“核心群”可以降低层次分析法的复杂程度。第三，目前的教育评价一般从知识与技能，过程与方法，情感、态度与价值观三个维度讨论，但是科学的目的不是评价，在考核评价中应更多遵从教育规律，学生党员发展量化考核要符合学校特点和学校层次发展程度。