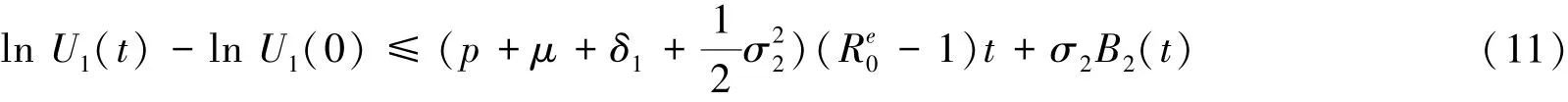未接受治疗吸毒者的随机生存性分析

江慧,魏凤英

(福州大学数学与计算机科学学院,福建福州 350108)

0 引言

毒品不仅伤害吸毒者自身健康,而且传播疾病,严重地影响了社会治安[1-2].为了协助决策者更好地预测和控制吸毒者的数量,有效地使用治疗资源并减少吸毒者的数量.本研究在White近期提出的由常微分方程组刻画的吸食海洛因人口模型[3]的基础上,针对总人口数量较大的实际情况,常数输入率不能满足刻画易感者数量增长的趋势,借鉴SEIR模型和SIR模型采用的饱和发病率,以及传染病模型引入随机干扰的方法[7-11],建立了未接受治疗吸毒者的随机生存模型：

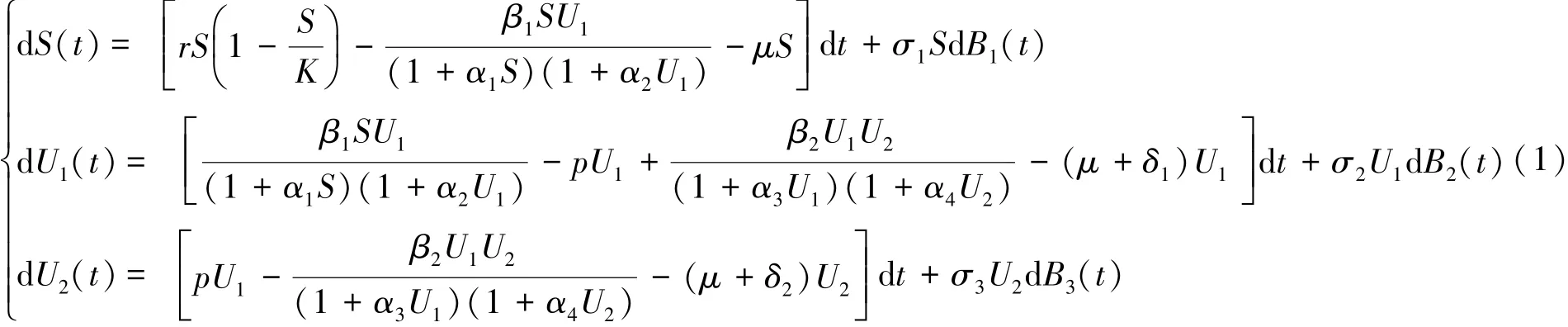
其中：S(t)为t时刻易感者数量；U1(t),U2(t)是未接受治疗和正在接受治疗的吸毒者数量,且总人口数为N(t)=S(t)+U1(t)+U2(t).

假设易感者数量远大于吸毒总人数；β1是易感者转变为未接受治疗的吸毒者比率；β2是正在接受治疗的吸毒者转变为未接受治疗的吸毒者比率；μ是人口的自然死亡率；p是吸毒者接受治疗的比率；δ1是去除率(未接受治疗的吸毒者因吸食毒品死亡或自发恢复的比率,自发恢复后,吸毒者不再复吸)；δ2是成功治愈率(成功治愈后,吸毒者不再复吸)；Bi(t)是独立标准布朗运动且Bi(0)=0,＞0(i=1,2,3)为白噪声的强度.

1 正解的全局性和唯一性

定理1 对任意(S(0),U1(0),U2(0))∈,系统(1)存在唯一正解(S(t),U1(t),U2(t))∈R3+.

证明 由文献[12]的定理2.1可知,只需证明存在一个二次可微函数V,使得LV≤Q,其中Q为正常数.现定义一个二次可微函数V：

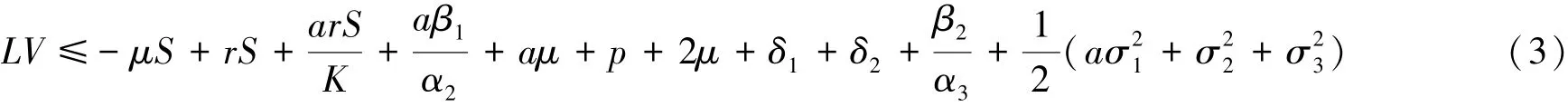
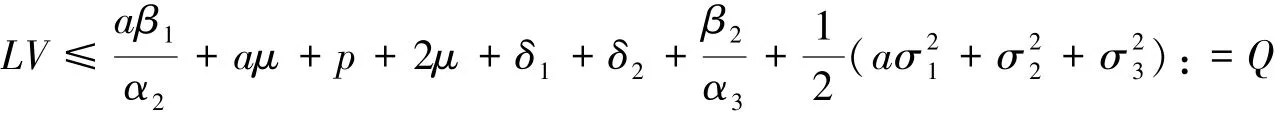
2 持久性

引理1对任意的初值(S(0),U1(0),U2(0))∈,系统(1)的解(S(t),U1(t),U2(t))∈R3+具有以下性质：

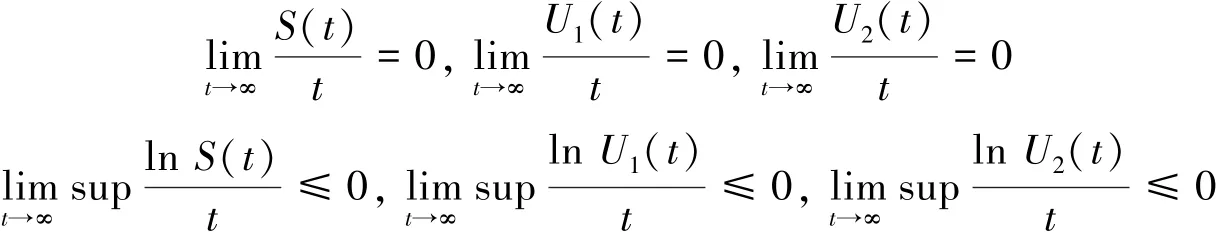
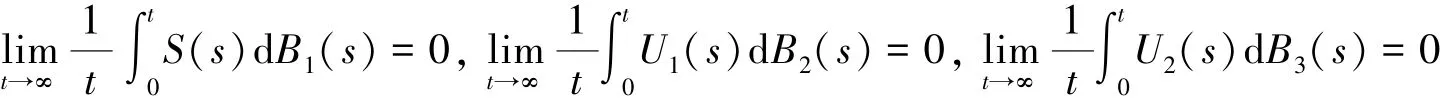
定理2若＞1,2r＞,则inf A 〈U1〉t≥ B(-1) ＞ 0.其中：

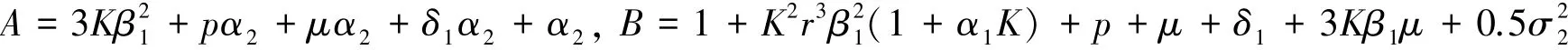
证明 定义一个二次可微函数V1：→R：V1(S,U1)=c1S-ln U1-α2U1.应用Ito)’s公式

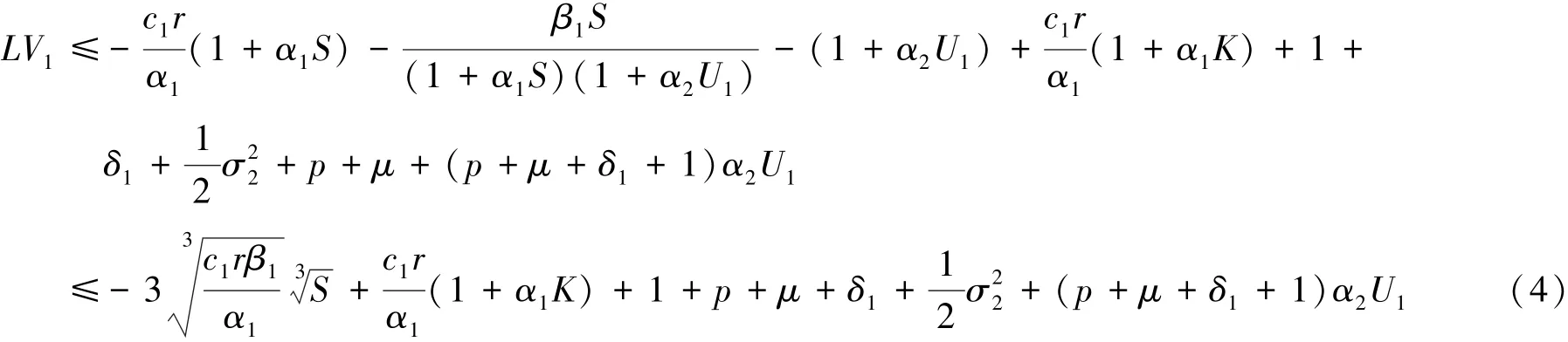
取V2(S)=,应用It’s公式以及文献[15]的引理4.2可得：

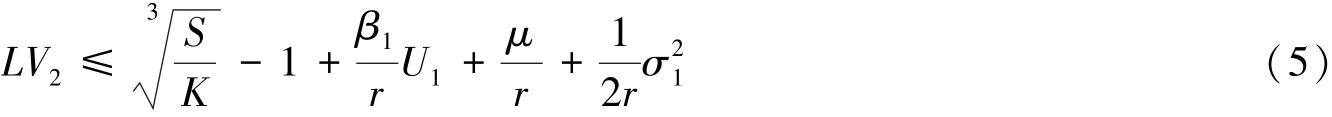
令V3(S,U1)=V1(S,U1)+3V2(S),则有：

取 c1=K2r2β21α1, 则=Krβ1.那么：

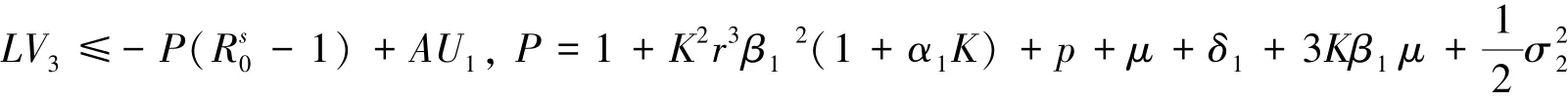
则存在：

对等式(7)两边同时取积分平均值,可知：

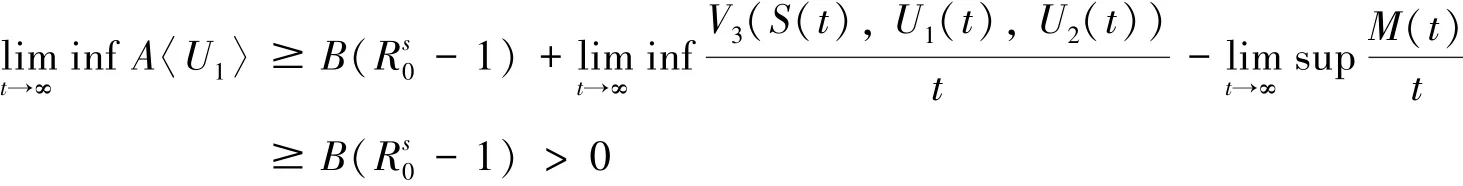
3 平稳分布及遍历性

定理3若＞1,则系统(1)存在平稳分布,且正解是遍历的.其中：

证明 易证文献[16]引理3的条件(1)成立.为了证明条件(1)成立,只需证明对任意(S,U1,U2)∈＼Dε,存在一个非负二次函数V和一个邻域Dε,使得LV≤-1.定义：

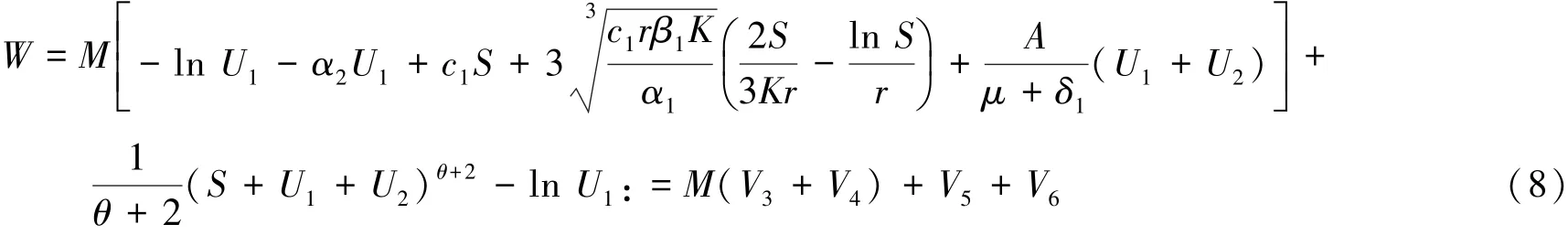
显然,函数W(S,U1,U2)是连续函数,因此W(S,U1,U2)在内部有最小值(S*,,).

定义一个非负二次可微函数V=M(V3+V4)+V5+V6-W(S*,,,应用It’s公式可得：

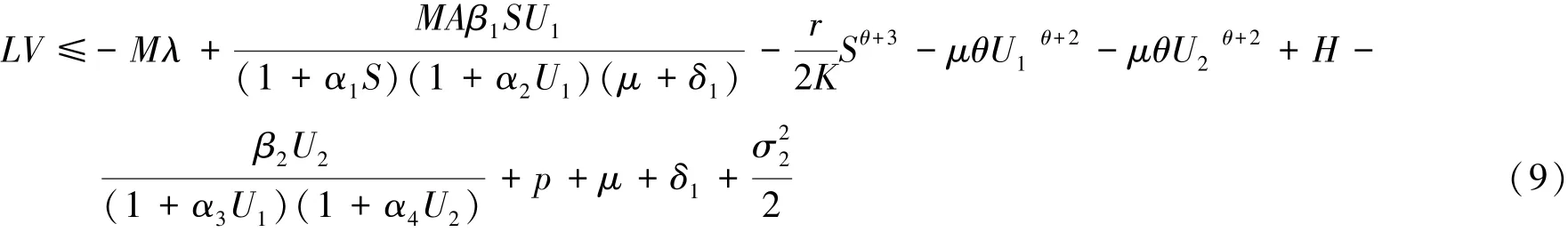
接下来定义一个有界闭集Dε如下：

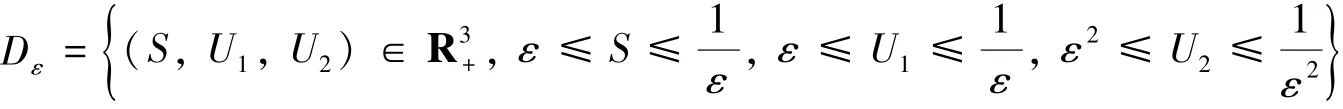
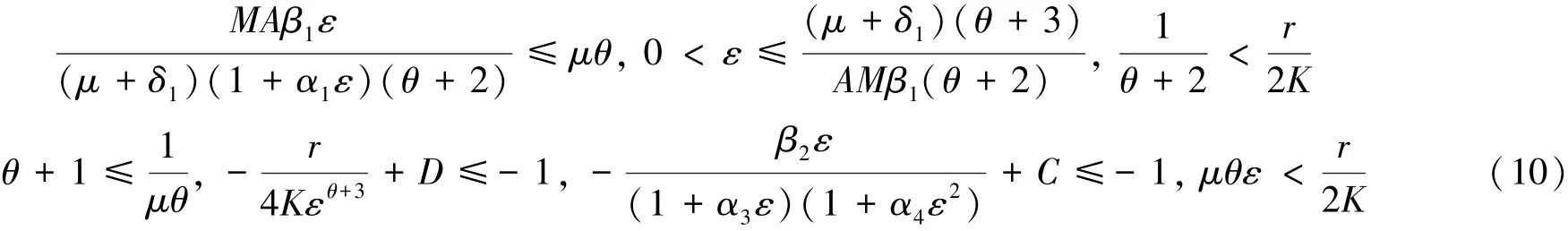
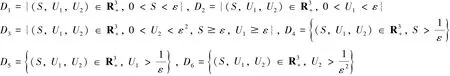
情形1、2、5、6易于证明,此处从略.

情形3.若(S,U1,U2)∈D3,则：

其中：

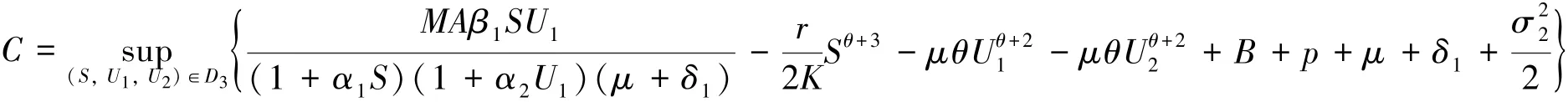
情形4.若(S,U1,U2)∈D4,则：

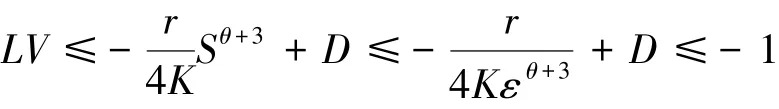
其中：

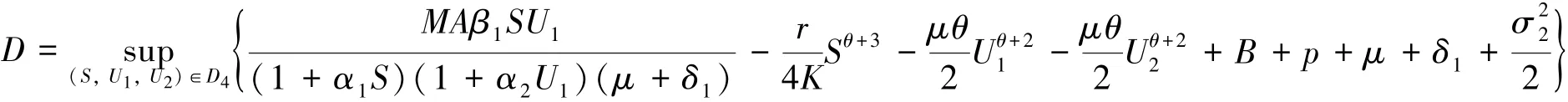
综上,当(S,U1,U2)∈＼Dε时,LV(S,U1,U2)≤-1成立.

4 绝灭性

定理4若＜1且2μ ＞,=max{,i=1,2,3},则U1(t)=0,U2(t)=0.