一种基于短时时域分析的侧信道信号预处理方法*
何卫国,饶金涛,李 军,李雨励,黄金金
(成都三零嘉微电子有限公司,四川 成都 610041)
0 引言
传统的密码分析侧重于密码算法本身的数学特征,而忽略了密码设备在运行密码算法过程中泄露的物理信号。自1996 年Paul Kochers 首次提出利用时间分析密码设备中的敏感信息的思想以来[1-2],侧信道分析受到了人们的极大关注,且相关研究已经成为密码学研究的一个重要分支,被广泛应用在密码芯片的攻击检测领域。侧信道攻击的基本原理是用过采集密码设备在运行过程中的能量信息或者电磁信息,通过统计分析的方法恢复密钥信息。
在进行侧信道攻击的过程中,需要对采集到的密码设备的侧信道信号进行预处理。采集到的侧信道信号是非平稳、时变、离散性大、信息量大的复杂信号,对于攻击检测人员来讲处理难度较大。因为侧信道信号携带各种信息,是一个未知的信号。目前的研究表明,采集到的侧信道泄露信号与密码设备运行的时钟频率、处理的数据、进行的操作有较大关系[3-5]。
本文针对目前侧信道信号预处理的方法不够灵活、需要大量的参数配置等缺点,提出了一种具有普适性的侧信道信号预处理方法,有效提高了侧信道攻击的效率。
1 基本理论
1.1 短时域分析
短时分析技术主要处理语音信号,基本原理是用平稳信号的处理方法处理非平稳信号。侧信道信号虽然具有时变特性,由于电容的充放电在一个短时间范围内基本特性基本保持不变,因此侧信道信号也具有短时平稳性。类比分析可以得知,运用短时分析技术对侧信道信号进行预处理完全可行。
常见的短时处理方法有短时平均能量分析、短时平均幅度分析以及短时过零检测等基本方法,本文主要利用短时平均能量对侧信道信号进行预处理。短时平均能量分析主要用于非平稳信号的处理,基本定义如下:

En代表一个分段信号的能量,通过式(1)可以得知。短时平均能量相当于信号的平方通过一个单位函数响应为h(n)的线性滤波器的输出。同时,不同窗口的选择将决定短时能量的特性。常见的窗口有汉宁窗、海明窗、直角窗以及高斯窗等。直角窗的谱平滑较好,但波形细节丢失,与海明窗刚好相反。另外,窗口长度对于能否反映信号的幅度变化起决定作用。如果窗口很大,等效于带宽很窄的低通滤波器,此时En随时间的变化很小,不能反映信号的幅度变化,波形的变化细节无法观测;反之,窗口太小,滤波器的通带变宽,短时能量随时间有急剧变化,不能得到平滑的能量函数。
1.2 基于能量的侧信道相关性分析
能量攻击分析是侧信道攻击中最有效的方法之一,其中相关性能量攻击最具代表性。本节主要对相关性能量分析攻击进行描述。2004 年,Eric Brier等提出了相关性攻击分析[3]。相关性攻击分析主要利用了统计学中的皮尔逊相关系数ρ,攻击流程如下:
(1)在密码设备中,将N组不同的输入数据和存储在密码设备中的敏感信息(密钥等)进行运算,同时获取密码设备在运算过程中的能量消耗记为H;
(2)通过猜测敏感信息,产生相应的假设中间值,然后根据假设中间值的汉明重量或者汉明距离,计算得到假设的能量消耗记为W;
(3)计算H和W之间的线性相关系数:
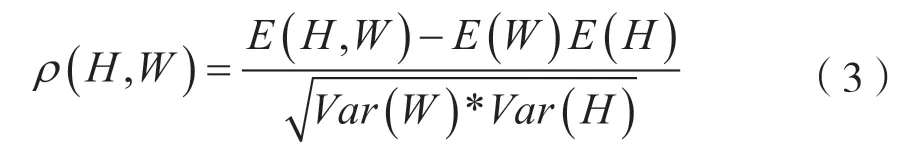
式中,E(·)表示期望,Var(·)表示方差。当ρ的绝对值最大时,对应的猜测敏感信息即为正确的敏感信息。
2 基于短时域预处理方法
利用短时能量分析对侧信道信号进行预处理。采集的侧信道信号主要以电压信号为主,令某段时间采集到的电压信号为U=(u1,u2,…,ut),利用短时分析的方法实现电压的平方操作,将其转化为功率信号,同时进行窗口函数的滤波操作,具体的思路如图1 所示。

图1 短时域侧信道信号处理流程
(1)设置侧信道信号采集的基本环境。设示波器当前采样频率为f,密码设备运行的时钟频率为fs,采集到的侧信道信号的点数为M,条数为N。信号矩阵为TN*M;
(2)确定选择所用窗函数窗的大小,窗的大小以密码设备的运行时钟为单位,计算方法为n=f/fs;
(3)根据窗的大小n对信号矩阵进行短时能量分析,直到信号矩阵的每行计算完成;
(4)完成所有行的短时能量分析后,得到新矩阵T´。
3 实测分析
3.1 测试环境
实测环境主要采用SASEBO-G 侧信道测试评估分析板,如图2 所示。SAKURA-G 能量分析评估板主要是对实现的算法模块进行侧信道信息泄露进行评估测试。它由两块FPGA 芯片构成:一块实现算法,型号为XC6SLX75;另一块实现控制逻辑,型号为XC6SLX9。在实现算法的FGPA 芯片的VCC端串接一个1 Ω 的电阻,通过差分探头可以监测电阻上电压信号的改变,从而可以测试运算逻辑在运行过程中的能耗信息。

图2 SAKURA-G 侧信道能量分析评估板
3.2 实测结果
在FPGA 上实现SM4 算法,利用示波器采集SM4 密码算法在运算过程中产生的能量消耗。实验中,测试的目标主要是分析SM4 算法的攻击测试,对比分析使用短时能量分析和没有使用短时能量分析的情况。
图3 为采集的SM4 密码算法在运行过程中产生的功耗,图4 为经过滑动平均处理后的曲线,图5为经过短时域三角窗处理后的曲线,图6 为经过汉明窗短时域处理后的曲线,图7 为经过矩形窗短时域预处理的曲线,图8 为经过高斯窗短时域预处理的曲线,表1 为在不同条件下处理后进行攻击获取第一轮子密钥所对应的相关性系数。

图3 SM4 算法原始曲线

图4 滑动平均处理后的曲线
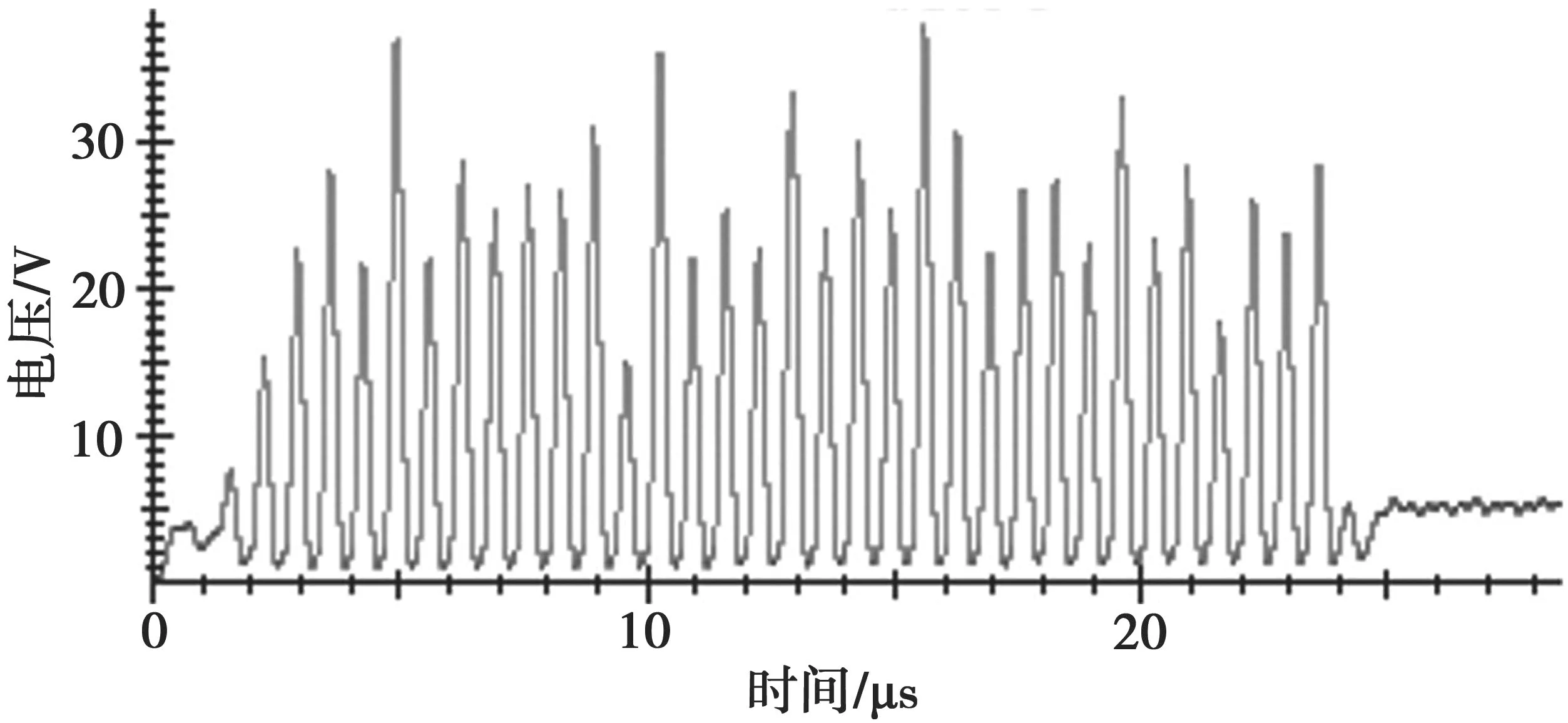
图5 三角窗短时时域处理后的曲线

图6 汉明窗短时时域处理后的曲线

图7 矩形窗短时时域处理后的曲线
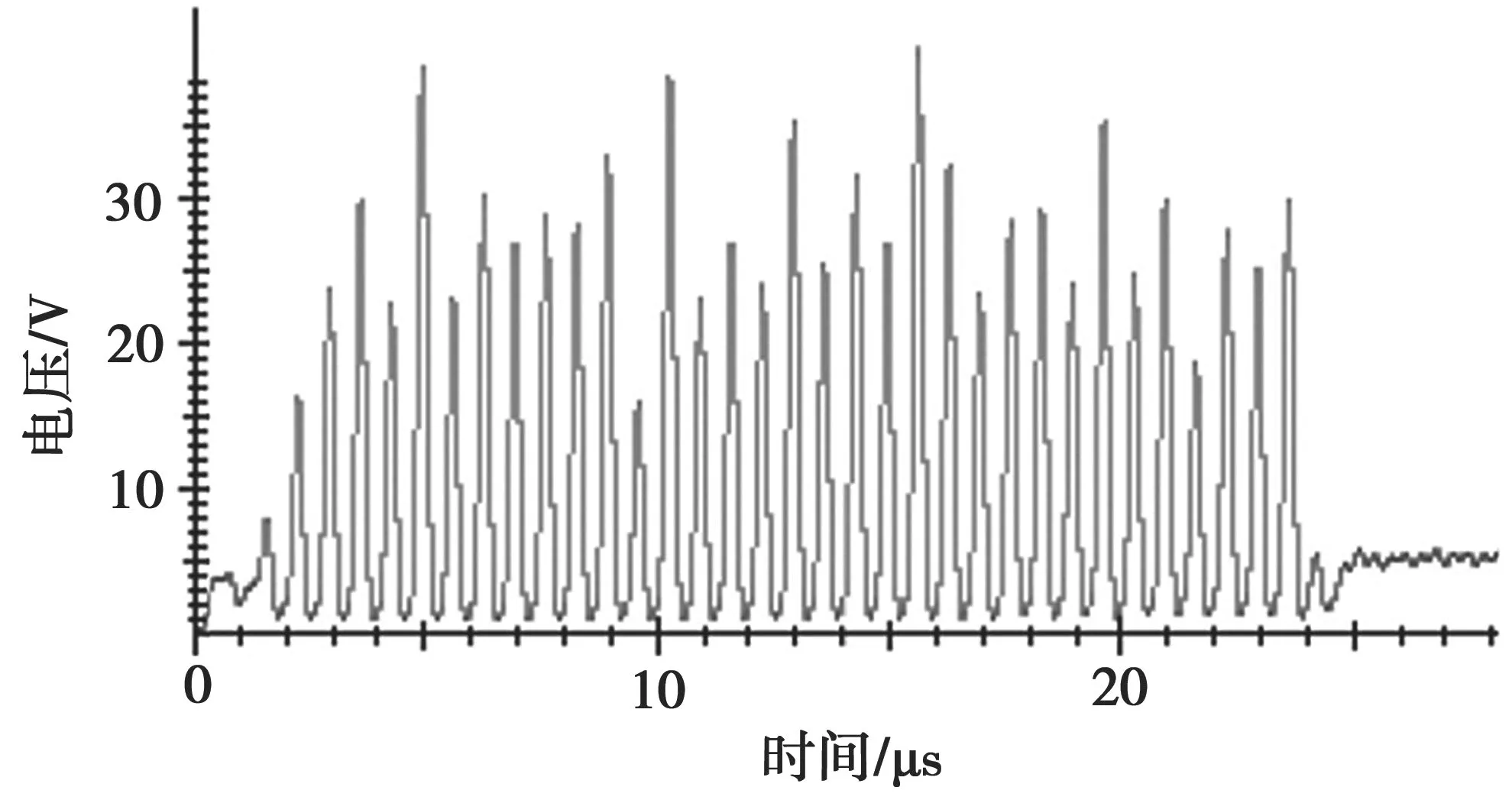
图8 高斯窗短时时域处理后的曲线

表1 实际的攻击结果对比
实验结果分析表明,经过短时时域预处理的曲线信号轮廓更加清晰,其中高斯窗对信号处理的效果最好,攻击后所得正确的密钥对应的相关性系数最高,具有较高的辨识度,从而进一步提高攻击正确性和效率。
4 结语
本文提出了一种基于短时时域分析的侧信道信号预处理的方法,并进行实测攻击分析。实验结果表明,所提预处理方法大大提高了攻击信号的信噪比,从而大大提高了攻击成功率。

