基于CNN-BiLSTM 的短波通信频率预测研究*

夏吉业，张海勇，徐 池，贺 寅

（海军大连舰艇学院，辽宁 大连 116018）

0 引言

短波通信自上世纪初出现以来，就一直被广泛的应用于无线通信中，在远程通信方面，相比于卫星通信，短波通信能够不依靠中继用较小的发射功率达成通信，此外，短波通信在军事通信中也占据着重要地位[1-2]，发展短波通信意义重大。

短波远程通信是通过电离层反射实现的，受电离层色散、时变[3]等特性及信道传输过程中存在的多普勒频移、衰落、多径时延、噪声干扰[4]等现象影响，只有选择适当的通信频率，才能使通信过程在优质信道中达成，保证短波远程通信的通信效果。因此，实现精准的通信频率预测在短波远程通信过程中尤为重要[5]。

传统频率预测方法主要有国际无线电咨询委员会（CCIR）推荐方法（即340 报告）和亚大预测[6]，通过公式来进行计算的方法进行预测，之后国际电联通信大会（ITU-R，即原CCIR）给出三个短波信道模型，即报告252、报告252 补编和报告894[7-8]。随后国外推出了一系列频率预测程序，主要有IONCAP、VOACAP、PropMan、NTIA/ITS 以及W6ELProp 等[5]，这些预测程序针对不同的适用环境和条件，在一定程度上提高了预测精度，但主要是在理想模式下进行的，对气候、太阳活动、电离层跳变等不确定因素不能很好估计[9]。在国内方面，2007 年中国电波传播研究所结合亚大地区电离层探测数据，对亚大模型进行改进，有效的提高了该地区频率预测的精度[10-11]，但受地域限制，该方法在通信距离超过4000 公里时的预测精度较低，基本不能满足远程通信时对通信频率的预测需求。

随着机器学习和人工神经网络算法的出现和发展，从本世纪初开始，研究者们利用人工神经网络强大的非线性预测能力，将其引入到短波频率预测领域，并获得了一些成果。最初的方法是用反向传播（BP）神经和网络预测f0F2 月中值[12]，预测误差在0.3 MHz以上，在太阳黑子周期剧烈变化时甚至达到1 MHz 以上；简相超[13]等人将混沌理论和神经网络相结合方法，构成混合模型来进行短波频率参数预测；金会彬[14]等人基于神经网络的foF2 预测方法，提高了对电离层暴期的预测结果；任淑婷[15]等人提出基于模糊小波神经网络[16-18]的短波频率预测模型；赵德群[9]等人提出思维进化小波神经网络（MEA-WNN）与混沌理论相结合的短波通信频率预测方法，提高对f0F2 的预测精度。上述算法均存在一些缺陷，主要体现在对数据的处理太过复杂、对参数要求较为苛刻、选择神经网络模型存在收敛慢、梯度消失或爆炸等问题。为避免神经网络在反向传播时产生的梯度消失，结合挥深度学习算法[19-20]对处理非线性时间序列的独特优势，2019年张雯鹤[21]等人提出一种基于长短期记忆神经网络（LSTM）模型预测f0F2 的方法，该模型具有收敛速度快、收敛性较好等特点，但仅对f0F2 月中值实现了预测和验证；同年，尚教凯[22]等人基于LSTM 模型实现对未来24 小时的点对点远程短波通信可用频率预测，但该方法使用单特征输入时预测耗时较长，使用多特征输入时结果存在时延，仍有提升空间。

为解决上述问题，本文提出一种基于卷积神经网 络（Convolutional Neural Network，CNN） 和 双 向长短期记忆神经网络（Bidirectional Long Short Term Memory，BiLSTM）相结合的模型，即CNN-BiLSTM模型，来实现对远程短波通信频率的预测。

1 CNN-BiLSTM 模型的提出

1.1 卷积神经网络（CNN）

卷积神经网络（CNN）通过原始数据与卷积核相乘来提取局部特征，在一个网络中可以通过选择多种类型卷积核来达到提取多个局部特征的目的，因此CNN 相比其他网络，其提取布局特征的能力更为突出。该网络主要由卷积层、池化层和全连接层组成。其中，运用卷积核对原始数据进行卷积操作来提取特征的过程发生在卷积层，该层是CNN 网络的核心层，其过程可用式（1）表示。

式中，σ为激活函数；⊗ 为卷积操作；W为权值矩阵；b为偏置矩阵。

池化层的作用是将卷积层得到的输出通过池化操作来对处理后的数据进行压缩，提高泛化能力。本文模型选用最大池化函数对卷积结果进行池化操作，通过取最大值来完成对局部特征区域的数据压缩过程，其过程如式（2）：

式中，di为通过卷积层提取的特征，m为池化宽度。

全连接层的作用是将前边网络提取到的特征信息综合到一起，它的每个结点都连接着上一层的所有结点，因此其相关参数较多。通过全连接层使所提取的特征具有更高层的含义，从而达成该网络模型所要实现的物理意义。

1.2 双向长短期记忆神经网络（BiLSTM）

长短期记忆神经网络(LSTM)最早由Hochreiter[23]于1997 年提出，是在循环神经网络（RNN）上的一种改进，在RNN 基础上引入记忆模块，在提高了计算效率[24]的同时，有效的解决了RNN 出现的梯度消失或者爆炸问题[25]。

LSTM 模型具有较好的非线性时间序列的处理能力，但在实验过程中发现，LSTM 的记忆能力有一定限度，并且该模型是一个单向传递的过程，即后一时刻的状态对当前时刻没有任何影响，而在短波通信频率预测过程中，认为在一定的时间间隔内，频率的预测可以综合考虑前、后时刻的输入和状态，来提高预测效果。因此，本文引入双向长短期记忆神经网络（BiLSTM），该模型将两层不同的LSTM 互连，使每个输入都会从正反两个方向经过网络，该模型一方面增强了处理非线性时间序列的能力，另一方面也能进行更充分的学习训练，利用当前输入和后一时刻的状态进行短波频率预测，因此在理论上有更好的预测效果。BiLSTM 模型结构如图1 所示。

图1 双向长短期记忆神经网络结构

该模型的运算结果如式（3）、式（4）所示。

1.3 Dropout 运算

在CNN 网络运算过程中，为精确的逼近训练数据的局部特征，容易出现过拟合现象，为解决这一问题，本文提出的模型在CNN 网络之后进行Dropout 运算。该算法由Alex[26]等人于2012 年提出，原理是在每个训练批次中，适当忽略部分特征检测器，减少相互作用，因此在网络运行过程中不会太过依赖某些局部特征，有效的降低模型过拟合，从而增强了模型的泛化能力。使用该算法的神经网络模型与标准神经网络模型的对比如图2 所示。

图2 标准神经网络与Dropout 网络模型对比

该算法由于忽略部分检测器，使当前层的检测器无需遍历下一层的每个检测器，降低了网络模型的复杂程度，因此该算法在解决过拟合现象的同时，也大大减少了网络模型的运算时间。综合考虑历史经验及多次尝试，在本文的模型中使用该算法忽略的检测器比例为20%。

1.4 CNN-BiLSTM 模型

短波远程通信的最高可用频率受电离层特性影响，具有一定空间和时间上相关性，不少学者也在进行短波通信频率时间栅格和空间栅格尺度的研究。结合在本文中分析得到的CNN 具有较好的提取空间局部特征能力与BiLSTM 在处理非线性时间序列时独到的优势，提出基于CNN-BiLSTM 的融合模型短波通信频率预测模型，结构如图3 所示。

该网络模型主要可划分为输入层、CNN 层、Dropout 层、BiLSTM 层、全连接层和输出层，其中CNN 层和BiLSTM 层为本模型的核心结构，CNN 层是由多个一维卷积（Conv1D）层和一维最大池化（MaxPooling1D）层堆叠组成。利用该模型进行远程短波通信频率预测的过程如下。

将历史通信频率等相关数据集作为该网络的输入，经数据归一化、形成矩阵向量等预处理之后，进入CNN 层利用多层卷积核与池化核参数对相关频率数据进行局部深层特征提取，提取完毕后得到多组特征向量再经Dropout 层随机丢弃部分特征以提高模型的稳健性，随后将处理后的输出特征通过BiLSTM 网络进行训练，最后，将经BiLSTM 训练得到的输出结果进行拼接融合，再经全连接层进行信息综合后，得到模型预测的频率值。

图3 CNN-BiLSTM 模型结构

2 实验对比及分析

2.1 数据获取与处理

短波通信的历史数据是指通信双方在达成较稳定的短波通信过程中使用或设置的一些相关通信参数，包括通信时刻、双方位置、通信频率、通信功率等因素，由于该数据是实际通信过程中产生的，具有较高的可靠性和准确性，若能积累一定数量较为连续的历史数据，则可用来进行短波通信频率预测。受限于实际情况，无法得到足以支撑该模型需求的历史通信频率值作为样本数据，本文采用ITS/REC533 软件提取仿真数据，即2014 年8 月31 日09 时至2015 年1 月29 日08 时北京石景山到福建台江两点间，时间间隔为1 小时的短波最高通信频率数值，组成样本数据。该样本数据集共有3624 h数据，其中，前3600 h数据（共150 天）作为模型的训练样本，后24 h 数据作为模型的测试样本，数据格式如表1 所示。

2.2 模型效果评价指标

为对比预测结果的好坏，使用预测的均方根误差（RMSE）和模型运行时间作为评判标准。RMSE值越小，所用时间越短，就代表该模型预测的效果越好。其中，RMSE 的计算公式如式（5）所示：

式中，yt和分别为t时刻的通信频率真实值和预测值，N为测试集的尺度。

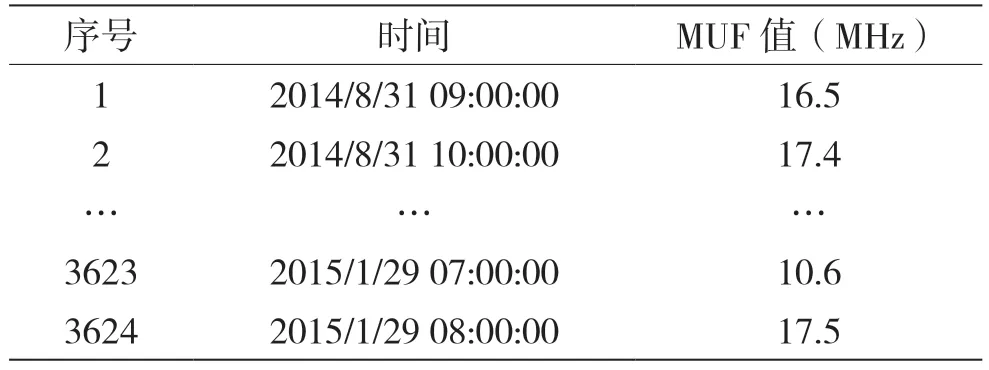
表1 样本数据表

2.3 预测结果与对比分析

单特征输入LSTM 模型、多特征输入LSTM 模型与本文提出的CNN-BiLSTM 模型进行短波通信频率预测的结果如图4、图5、图6 所示。

图4 单特征输入LSTM 模型预测结果

图5 多特征输入LSTM 模型预测结果

图6 CNN-BiLSTM 模型预测结果

图中虚线为通信频率的真实值，实线为通信频率的模型预测值，这三种模型的RMSE 和模型运行时间如表2 所示。

表2 三种模型RMSE 及运行时间对比

对比上述图表可以发现，在模型预测的准确性方面，单特征输入LSTM 预测模型RMSE 值仅为0.204，准确度最高，从图形中可以看出除初始1-3 h 的预测结果存在1 MHz 左右误差外，与真实值吻合较好；CNN-BiLSTM 预测模型RMSE 值为0.544，准确度次之，在预测MUF 值的高、低点存在1 MHz 左右的误差外，基本与真实值保持一致；多特征输入LSTM 预测模型RMSE 值为2.148，准确度最低，预测结果除初始1 h误差较大外，预测值与真实值存在约1 h 时延且有逐渐扩大趋势。在模型的运行时间方面，预测准确度较低的多特征输入LSTM 预测模型用时最短，仅为8.68 s；CNN-BiLSTM 预测模型次之，用时38.44 s；而准度度最高的单特征输入LSTM 预测模型用时最长，为203.22 s，是多特征输入LSTM 模型的23.4 倍，CNNBiLSTM 模型的5.3 倍。

综上所述，在短波通信频率预测方面，单特征输入LSTM 模型具有预测精度高，但费时较长的特点；多特征输入LSTM 模型极大的缩短了预测时间，但预测结果存在1 h 时延，预测效果得不到保证；本文提出的CNN-BiLSTM 预测模型在基本保证预测精度的基础上，极大的缩短了单特征输入LSTM 模型预测所用时间，又有效的解决了多特征输入LSTM 模型所存在的预测时延问题，因此该模型可用于短波通信频率预测。

在实际通信过程中，要想获得连续150 天的短波通信历史数据难度较大，对固定台站与移动台站、移动台站与移动台站间的短波通信而言尤为如此。因此，出于短波通信的实际考虑，如何在保证短波通信频率预测精度的基础上，尽可能的减少所需要的通信历史数据成为本文重点研究内容。

为减少对通信历史数据的需求，本文分别使用连续7 天、8 天、9 天、10 天、11 天、12 天，间隔1小时的仿真数据作为训练样本，后1 天的仿真数据作为测试样本，利用本文提出的CNN-BiLSTM 短波频率预测模型进行仿真实验，并与单特征、多特征输入LSTM 模型进行对比，实验结果如图7 所示。

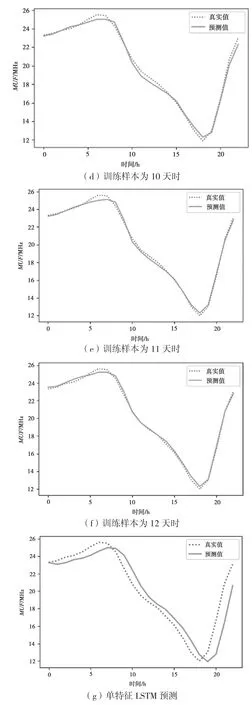
图7 短波通信频率预测效果

在图7 中，（a）～（f）分别表示训练样本为7-12天时的CNN-BiLSTM 模型仿真结果，（g）、（h）表示训练样本为12 天时，使用单特征输入LSTM 模型和多特征输入LSTM 模型的仿真结果，蓝色虚线为通信频率的真实值，黄色实线为通信频率的模型预测值。模型运行时间及误差如表3 所示。

表3 模型运行及误差表

从图（a）～（f）及上表中可以看出，在预测准确性方面，本文提出的CNN-BiLSTM 模型随训练样本天数的增加，预测精度不断增加，在训练样本数为12 天时，RMSE 值仅为0.227，除频率最高处存在0.5 MHz 的误差外，预测值与真实值基本吻合；在模型运行时间方面，随训练样本天数增加，模型运行时间基本呈递增趋势，但总体差距不大，最短运行时间与最长运行时间相差25.73 s；在样本最大误差率方面，随训练样本天数增加，误差率逐步降低，在训练样本为12 天时最大误差率低至3.08%。

从图（f）～（h）及上表中可以看出，在训练样本数为12 天时，单特征输入LSTM 模型和多特征输入LSTM 模型的预测精度相对较低，预测最大误差分别为4.5 MHz 和5.2 MHz，最大误差率均达到20%以上，相比之下，本文提出的CNN-BiLSTM 预测模型在预测精度、最大误差以及最大误差率方面都有显著提升。由此可以得出，在训练样本数较少的情况下，CNNBiLSTM 预测模型的预测效果要优于单特征、多特征输入LSTM 预测模型。

综上所述，本文提出的CNN-BiLST 模型可实现对未来1 天的短波通信频率较为精准的预测，并且相对于单特征、多特征输入LSTM 预测模型，该预测模型在保证预测精度的同时，大幅缩减了对短波通信历史数据的数量要求，增加了在实际短波通信过程中的适用性。

3 结语

本文概述了通信频率预测发展现状及存在问题，提出了CNN-BiLSTM 模型用于远程短波通信频率预测，并与单特征、多特征输入LSTM 预测模型进行了对比仿真实验，验证了该模型可用于短波通信频率预测，在训练样本数较少的情况下，该模型的预测精度优于单特征、多特征输入LSTM 预测模型，对短波远程通信频率的预测研究具有一定借鉴意义。该方法基于短波通信的历史数据进行通信频率预测，如何更好的采集存储历史数据以及对历史数据的处理利用等方面还值得进行进一步研究。