基于时变扩散系数的圆柱体煤屑的瓦斯放散规律研究

蔡银英，程建圣，程 波

(1.重庆第二师范学院，重庆 400067； 2.中煤科工集团重庆研究院有限公司，重庆 400037)

我国煤层气(也称为“瓦斯”)资源丰富，“十三五”期间，在国家相关利好政策的驱动下，将开启煤层气资源开发利用的新时代。研究瓦斯在煤中的扩散规律，有助于进一步认识煤层气运移机理，为煤层气开发方案的制订提供依据，同时对于研究井下瓦斯含量的测试方法，以及预测煤与瓦斯突出危险性，具有非常重要的现实意义[1]。一般认为，瓦斯以“吸附”和“游离”的形态赋存于煤体内部的孔隙和裂隙通道内[2-3]。在煤体原有的“吸附—解吸”的平衡状态被打破后，煤孔隙内的瓦斯在浓度差的驱动下，逐渐扩散至煤的裂隙通道内[4-9]。在研究煤屑瓦斯放散规律方面，大多数学者采用了理论分析并结合实验测试的方法，如杨其銮等[4-5]以菲克扩散定律为基础，建立了球形煤屑瓦斯扩散的数学模型，并求取了方程的理论解，为我国学者研究煤屑瓦斯扩散规律奠定了基础；此后，何学秋[6]、聂百胜[7]等分析了瓦斯在煤体内扩散的微观机理，并指出瓦斯扩散的模式；聂百胜等[8-9]考虑煤屑界面传质的影响，建立相应的瓦斯扩散数学模型，求取了解析解；秦跃平[10-11]、王健[12]等通过对达西定律与扩散定律的比较，认为瓦斯在煤屑内运移的驱动力为压力差；张飞燕[13]、韩颖[14]等建立了球形煤粒的瓦斯扩散方程，并推导了相应的无穷级数解，测定了煤屑瓦斯在整个解吸期间的扩散过程；杨涛[15]、刘彦伟[16]等开展了温度与扩散系数之间关联性的研究；李树刚[17]、赵东[18-19]等采用实验的方法分别研究了低频振动、注水对煤体瓦斯解吸特性的影响；刘高峰等[20]分析了气肥煤、焦煤的孔隙特征，并对CH4/CO2混合气体在煤体内的吸附—解吸特征进行了研究；李小春等[21]研究了有效应力对煤吸附特性的影响，并获得了考虑有效应力影响的Langmuir方程形式；刘彦伟等[22]研究了软硬煤粒瓦斯扩散速度、扩散系数的差异特征随粒径的变化规律，并分析了粒径对软硬煤瓦斯扩散行为产生差异性影响的机理；李志强等[23-25]研究指出煤屑瓦斯的扩散系数为与时间相关的函数，并通过实验的方法，获得了扩散系数的时变规律。

综上所述，国内外学者已针对瓦斯在煤屑内的流动规律开展了大量的研究，一般认为瓦斯在煤粒内的运移过程服从菲克扩散定律，即扩散速度与浓度梯度成正比。但煤本身也是一种多孔介质，在煤体内瓦斯含量降低的过程中，煤体自身的孔隙结构也会随之而发生改变[26]，李志强等[23-25]研究证实在煤屑放散瓦斯的过程中，其扩散系数为一个时变量。因而，在进行煤屑瓦斯放散规律的研究时，将经典模型中的扩散系数设定为时变参数将更能反映煤屑瓦斯放散的实际情况。并且，当前的研究成果大多将煤屑假设为球形煤粒[4-11,13-16,23-25]，但在研究的过程中，对大量煤样破碎后的煤屑运用ThunisA688扫描仪观测发现，大部分煤屑为圆柱体或长方体，粒径一般为0.20～0.25 mm，少量煤屑为球形。因此，未考虑时变扩散系数及煤屑形状对煤屑瓦斯放散规律的影响，势必将导致理论分析与实验测试结果的相互验证出现偏差。同时，由于大多数煤屑呈圆柱体和长方体状，且当煤屑粒径极小时长方体煤屑的外形接近于圆柱体，故研究圆柱体煤屑的瓦斯放散规律将更接近于实际。

鉴于此，笔者首先对煤屑瓦斯放散过程中扩散系数的时变特性进行分析，并以此为基础，建立基于时变扩散特性的圆柱体煤屑的瓦斯扩散方程，利用数学物理的方法求取方程的解析解，再结合实验测试对解析解的准确性进行验证。

1 煤屑放散瓦斯时变扩散特性的理论分析

瓦斯在煤屑内的扩散，其本质是瓦斯气体分子不规则热运动的结果，以浓度差作为驱动力，使得瓦斯气体分子自高浓度区域扩散至低浓度区域。扩散系数本质是反映瓦斯气体分子在煤屑内运移阻力大小的一个指标。在煤屑放散瓦斯的初期，瓦斯气体分子沿扩散方向的浓度值存在不连续平衡势差，随着瓦斯气体分子的运动和碰撞，最终浓度分布会达到较为连续的稳定状态。

根据分子动力学与统计学理论，对瓦斯气体分子在煤屑内的扩散过程进行分析。首先假设煤屑内的瓦斯为理想气体，并且瓦斯气体分子在煤固体表面上发生的碰撞为弹性镜面反射，则瓦斯气体分子的平均速率为：

(1)

式中：R为气体状态常数；T为热力学温度；M为气体分子质量。

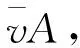
2 圆柱体煤屑放散瓦斯的数学模型

假设煤屑为半径R0、高度2h0的均质圆柱体。吸附平衡时，煤屑中的瓦斯浓度为C0，而后突然卸压至1个大气压，煤屑表面的瓦斯浓度为C1。瓦斯自煤屑内部向圆柱体的环形与轴向方向上扩散(如图1所示)，且扩散系数与放散时间相关，设时变扩散系数为Dt。

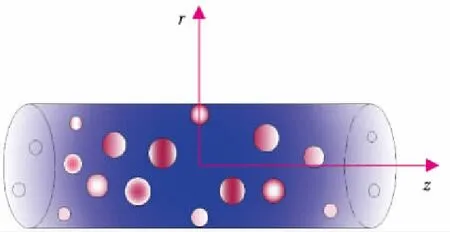
图1 圆柱体煤屑放散瓦斯示意图

圆柱体煤屑放散瓦斯的数学模型为：

(2)

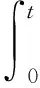
(3)

设式(3)中CN的解满足形式：CN=S(r)·H(z)·L(f)，且S(r)、H(z)、L(f)分别仅为r、z、f的函数。将CN=S(r)·H(z)·L(f)代入到式(3)中可得：

(4)

若式(4)成立，则等号左右两边均等于一常数，设其数值为-ε2，则可得关于f的解为：

L(f)=A2e-ε2f

(5)

式中A2为积分常数。

令-μ2使得式(6)成立:

(6)

则有：

H=B1cos(μz)+B2sin(μz)

(7)

式中B1、B2为积分常数。

将H(z)、L(f)的解代入到CN中可得:

CN=e-ε2f[B3cos(μz)+B4sin(μz)]·S(r)

(8)

式中B3、B4为A2分别与B1、B2的乘积。

将式(3)中的边界条件代入到式(8)中可得B4=0。故CN为:

CN=e-ε2f·B3cos(μz)·S(r)

(9)

由于式(9)中μ的取值存在无数多个，故根据解的线性叠加原理可得：

(10)

式(6)第一个等号右边的项，可写为：

(11)

式(11)为典型的零阶贝塞尔方程，其通解为：

(12)

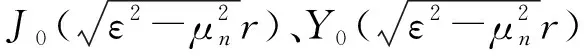
当r=0时，式(12)中的第二类零阶贝塞尔函数的取值将趋于负无穷大，因而CN也将趋于负无穷大。这势必与实际的初始边界条件相悖，因而积分常数N2的取值应为0。故CN为：

(13)

同样根据解的线性叠加原理可得：

(14)

将式(3)中的初始条件代入到式(14)中可得：

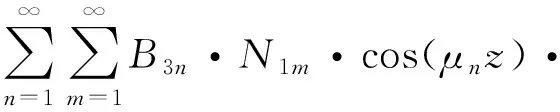
(15)

对式(15)进行积分处理，可得：

B3n·N1m=(C0-C1)·

(16)

将式(16)代入到式(14)中即为放散过程中圆柱体煤屑内瓦斯浓度的分布式。将煤屑的半径、高度代入到浓度分布式的解析解中，即可获得不同时间所对应的瓦斯放散量。

3 实验验证

实验所采用的煤样取自河南焦煤能源演马庄煤矿27131工作面，煤样的灰分为17.52%，挥发分为8.74%，真密度为1.65 g/cm3，视密度为1.57 g/cm3，极限吸附瓦斯量为43.685 1 cm3/g，瓦斯吸附常数b为 1.647 1 MPa-1。经破碎、筛分后，选用粒径为0.20～0.25 mm的煤屑，质量为20.003 g。应用MATLAB软件的统计绘图函数Wblplot进行威布尔分布检验后，采用矩估计法和经验方法对威布尔分布的相关参数进行求解，得到煤屑的稳定形状是直径为 0.18 mm、长为 0.24 mm 的圆柱。本次实验煤样的吸附平衡压力为0.83 MPa，实验温度为30 ℃，实验测定方法与文献[22-25]相同。扩散系数的求取与球形煤屑瓦斯扩散系数的计算方法类似，不同之处在于首先假定圆柱体煤屑的扩散系数为一定值，利用获得的浓度分布解与极限瓦斯放散量即可完成对实验煤样瓦斯扩散系数的计算。实验结果如图2所示。

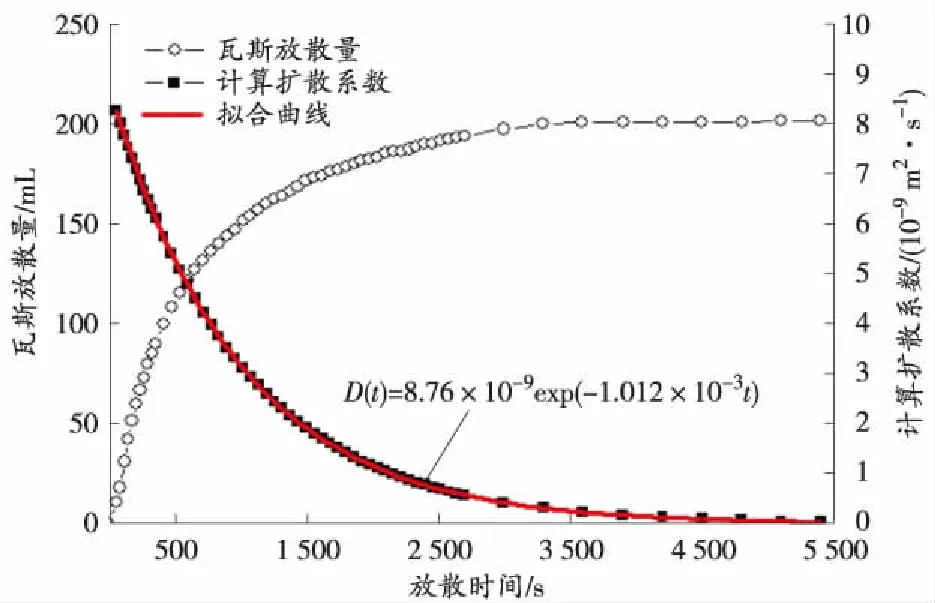
图2 不同时间煤样的瓦斯放散量与扩散系数

由图2可知，随着放散时间的延长，煤样的瓦斯扩散系数呈现衰减的特征，这与前人的研究成果一致。通过对不同时间扩散系数的拟合，发现二者极好地服从函数：

D(t)=D0exp(φt)

(17)

式中：D0为初始扩散系数，其值为8.76×10-9m2/s；φ为衰减系数，其值为-1.012×10-3s-1。

式(17)与李志强等[24-25]所提出的动扩散系数形式一致。应用式(17)所表征的时变扩散系数进一步对球形煤屑瓦斯放散规律进行检验对比，对比的球形煤屑的尺寸为直径0.20 mm和0.25 mm，结果如图3所示。

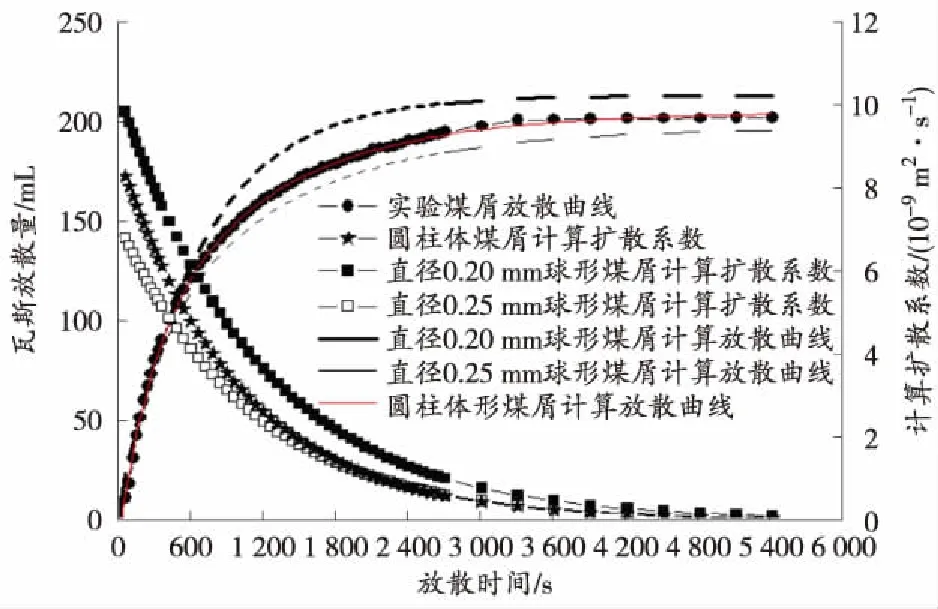
图3 圆柱体与球形煤屑放散曲线对比

由图3可知，基于直径0.20 mm和0.25 mm的球形煤粒的计算扩散系数与圆柱体煤屑的计算扩散系数变化特征相同，但具体数值不同，直径 0.20 mm 球形煤粒的计算扩散系数最大，圆柱体煤屑计算扩散系数次之。且采用球形煤粒的计算放散量与实际煤粒放散量误差较大，而应用基于时变扩散系数的圆柱体煤屑瓦斯扩散的数学模型计算值与实际较为吻合。这表明，煤屑形状的选取对于计算瓦斯扩散系数的影响较大，煤的物性参数对于其破碎、筛分后的粒度、形状影响较大，在研究煤屑瓦斯放散规律时，应针对煤屑的形状进行严格划分，以便使理论研究成果更接近于实际，有利于进一步厘清瓦斯扩散机理。这对于研究煤层瓦斯含量的井下快速测定、煤与瓦斯突出危险性预测指标具有极为重要的现实意义。

4 结论

1)对破碎煤屑形状进行观测，发现大多数煤屑呈现圆柱或长方体，且当粒径极小时长方体煤屑的外形接近于圆柱体，故研究圆柱体煤屑的瓦斯放散规律将更接近于实际。

2)建立了基于时变扩散系数的圆柱体煤屑瓦斯扩散的数学模型，采用数学物理的方法，求取了相应的解析解，可用于对试验数据的拟合，以及为井下瓦斯含量测定方法的研究提供理论依据。

3)通过实验室实验对获得的解析解进行了验证，结果表明：基于时变扩散系数的圆柱体煤屑瓦斯扩散的数学模型较球形煤屑更接近于实际。因此，在研究煤屑的瓦斯放散规律时，应根据破碎煤屑的大体形态对数学模型进行合理的选取，有助于进一步揭示煤屑瓦斯放散的机理。