基于正态信息扩散原理的极值型工程参数概率分布推断方法

宫凤强，王天成，黄天朗

(1.中南大学资源与安全工程学院，湖南长沙，410083；2.东南大学土木工程学院，江苏南京，211189)

在工程可靠度分析中，工程随机参数的最优概率密度或分布函数模型直接影响可靠度结果的准确性[1-2]，因此，对最优概率模型推断方法的研究始终是一项基础性工作[3-4]。在很多工程可靠度领域，经常遇到大量的极值型参数。所谓极值型参数，主要是考虑一系列最大(小)值参数，如建(构)筑物抗震设计中需要考虑的年最大地震荷载、海洋岩土工程中需要考虑的年最大风荷载等。当采用可靠度方法分析上述参数时，获取它们的最佳概率分布函数是首要步骤。目前，很多学者通常采用极值型分布对该类参数进行拟合检验。例如，张延年等[5]统计了中国159 个代表性城市在1951—2008年的历年最大风速，选取Gumbel(极值Ⅰ型)分布进行拟合分析；李凯平等[6]利用极值Ⅲ型分布拟合地震烈度；程思军[7]利用现场试验数据，对局部腐蚀钢筋的最大腐蚀深度进行概率统计，揭示Gumbel 分布可作为局部腐蚀钢筋的最大腐蚀深度概率模型。另外，一些研究者认为其他经典分布(正态分布、对数正态分布等)也可以用于拟合极值型参数的概率模型，如莫华美[8]研究最大积雪深度的概率分布时，认为对数正态分布代替极值Ⅰ型分布更具优越性；段忠东等[9]认为极值风速的最优分布为威布尔分布。从上述研究可知，极值型参数的最优概率分布并不一定是极值型分布，但是均从经典分布范围中选取。这种拟合方法存在以下2个不易解决的根本问题：1)区间不匹配。经典分布的定义区间一般为无限区间或半无限区间，但极值型工程参数的分布区间为有限数值区间，因此，利用经典分布拟合此类参数时在理论上无法满足累积概率等于1的要求。2)经典分布无法反映工程参数实际分布的随机波动性。经典分布均为单峰值型分布，但极值型工程参数的分布可能存在多个峰值，呈现一定波动性，因此，发展能够满足有限区间上累积概率等于1并能够体现实际分布随机波动性的概率分布推断方法十分必要。在这方面，很多专家提出了很多种推断方法。如苏永华等[10]提出了利用一般多项式推断岩土参数概率分布的方法；LI等[4]提出了正交多项式方法；张道兵等[11]运用最大熵原理估计了隧道衬砌结构参数的密度函数；李松辉[12]引入了车辆荷载效应的截尾分布模型。此外，HUANG等[13]在自然灾害风险分析中引入了信息扩散理论，目前该方法在岩土工程中得到了广泛应用。宫凤强等[14]利用正态信息扩散方法推断了小样本岩土参数的概率分布，取得了较好的拟合效果。周道成等[15]用正态信息扩散方法确定了河冰抗压强度概率分布，证明了正态信息扩散分布更加接近河冰抗压强度的真实分布，并优于经典分布的拟合方法；徐志军等[16]基于正态信息扩散理论，拟合了路基沉降的概率分布，并通过工程实例验证了此方法的正确性和有效性；黄达等[17-18]将正态信息扩散原理广泛用于推断岩体抗剪强度参数、岩体质量参数和粗粒土参数的单变量边缘分布，取得了良好效果；宫凤强等[19]利用正态信息扩散方法研究了Mohr-Coulomb 强度准则参数概率模型推断方法，其概率分布更加接近参数的实际分布规律。根据上述研究，本文作者提出基于正态信息扩散原理的极值型工程参数概率分布的推断方法，并考察该方法是否满足上述2个根本条件。在研究过程中，以样本个数分别为25和61的年最大标准风压样本和内摩擦角样本为例，分别采用正态信息扩散分布和Gumbel 分布进行拟合，对比分析2种分布拟合所得结果的优良性。在此基础上，利用模拟样本，考察样本个数对拟合精度的影响，并将正态信息扩散分布应用于2组核管道最大腐蚀深度的预测。

1 极值分布理论

极值理论研究的主要问题是极大(小)值的极限分布问题，是统计数学中的重要分支。设X1，X2，…，Xn为独立同分布的随机变量，分布函数为F(x)(称为底分布)，对自然数n，令Mn=max{X1,X2,…,Xn}，mn=min{X1,X2,…,Xn}，分别表示n个随机变量的最大值与最小值，则[20]

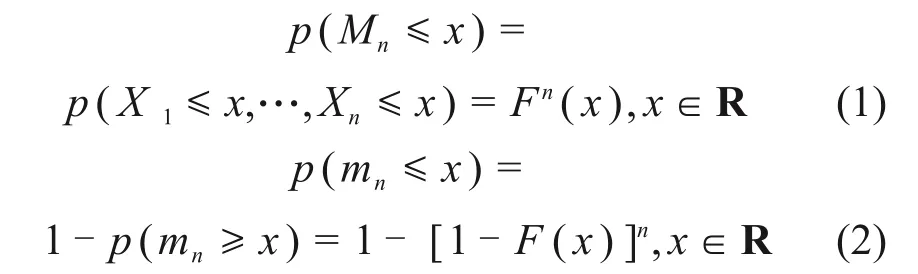
若已知分布函数F(x)，则可以根据式(1)和(2)精确求出最大值和最小值的分布函数。但在实际应用中，随机变量的分布函数F(x)往往是未知的，因此，很难直接用于统计分析。为求得原始样本的分布函数，必须考虑n→∞时分布函数的情况即极值渐进分布，简称极值型分布。

极值统计理论已经证明对于3种类型的连续型随机变量原始分布，根据其分布尾部的不同形式，当n→∞时，其极限分布只有3种类型，包括极值Ⅰ型(Gumbel)分布、极值Ⅱ型(Frechet)分布、极值Ⅲ型(Weibull)分布。其中，Gumbel 分布的概率密度函数和概率分布函数表达式见式(3)和(4)，其他2种分布的概率函数表达式见文献[20]。

2 正态信息扩散原理

设随机变量O的概率密度函数为f(x)，定义μ(x)在(-∞,+ ∞)上的1个波雷尔可测函数，Δn为常数且大于0，则称[13]

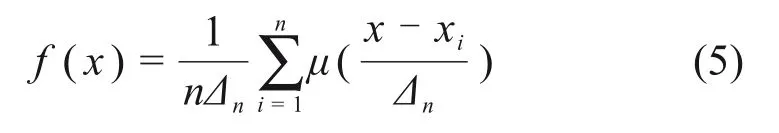
为总体密度f(x)的1 个扩散估计；μ(x)为扩散函数；Δn为总体密度f(x)的窗宽；n为随机变量的样本数；xi为样本观测值。根据信息扩散过程，μ(x)由下式确定：

式(6)满足式(5)对扩散函数的要求，且与概率论中正态分布的密度函数形式一致，称为正态信息扩散函数。将式(5)和式(6)联合求解，则随机变量O的概率密度函数f(x)的正态信息扩散估计为

3 截尾区间确定方法和实例样本

Gumbel 分布函数的定义区间一般为(-∞,+ ∞)，而样本工程物理力学参数的取值通常大于0 且其范围为有限区间。当用Gumbel 分布函数拟合这些数据时，必然存在区间不匹配问题。为了解决这个问题，基于“3σ”统计原则并考虑Gumbel 分布的不对称性，确定采用考虑偏度c的“3σ”分布区间截尾方法，具体的区间截尾公式见表1。

表1 截尾区间确定方法Table 1 Truncated interval determination method

选择高大钊[22]列举的年最大标准风压和张蕾等[23]列举的内摩擦角这2 种工程参数为例进行研究，具体数据见表2。

为了后续拟合检验计算的需要，对实际工程样本参数(如最值、平均值、标准差及偏度)进行统计，并计算相应的截尾区间左、右端点值，具体结果见表3。

4 2 种方法所得概率分布的对比分析

为了对比正态信息扩散分布与Gumbel 分布的拟合效果，从概率分布曲线、K-S检验值和累积概率3个方面进行具体分析。

4.1 概率分布曲线对比

图1(a)和图1(b)所示分别为2 组实际工程样本的累积概率分布曲线。从图1(a)可见：NID累积概率分布曲线与Gumbel 累积概率分布曲线在前半段几乎重合；在后半段，NID累积概率分布曲线完全沿着经验分布折线的变化趋势延伸，而Gumbel 累积概率分布曲线与经验分布折线的偏差较大。图2(a)和图2(b)所示分别为2组实际工程样本的概率密度函数曲线。从图2(a)可见，年最大标准风压样本的直方图反映了实际分布具有很大的波动性，而Gumbel 分布曲线呈单峰值型分布，显然无法很好地刻画实际分布的波动特性；NID概率密度分布曲线具有多峰值特点，更加贴近直方图的分布趋势。同理，对图2(b)的分析结果类似。综上分析可知NID概率密度分布比Gumbel分布更优。

4.2 K-S检验值和累积概率对比

表4 所示为2 组实际工程样本的K-S 检验值计算结果。根据K-S检验方法的特点，对2种工程参数的分布检验均在显著性水平为0.05(置信水平为95%)时进行。从表4 可见：在同一置信水平下，2组样本的K-S 检验法临界值分别为0.264 0 和0.174 0；NID 分布检验值的计算结果分别为0.127 2和0.043 8，而Gumbel分布检验值的计算结果分别为0.132 4 和0.054 5。显然，这2 组样本中NID 分布和Gumbel 分布的检验结果均通过临界值检验，但Gumbel 分布的检验值均比NID 分布的检验值高，这表明NID分布具有更优的拟合效果。

表2 实际工程样本数据Table 2 Sample data of actual engineering

表3 样本数据统计信息Table 3 Statistical information of sample data

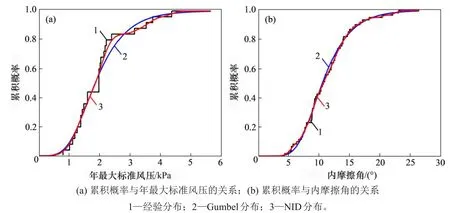
图1 实际工程样本的概率分布函数曲线比较Fig.1 Comparison of probability distribution function curves for actual engineering samples

图2 实际工程样本的概率密度函数曲线比较Fig.2 Comparison of probability density function curves for actual engineering samples

表4 实际工程样本K-S检验值和累积概率计算结果Table 4 Calculation results of K-S test values and cumulative probability for actual engineering samples

从表4还可见：根据确定后的截尾区间计算整个区间上的累积概率，对于Gumbel 分布，2 个实例样本所得到的累积概率分别为0.997 2和0.995 7，而NID 分布的累积概率均为1.000 0。上述结果表明在截尾区间下，Gumbel 分布无法满足累积概率等于1的先决条件。

5 样本个数对2 组分布拟合精度的影响

在实际工程中，所获得的样本很多都是小样本，很难考察不同样本个数对上述2种拟合方法在拟合精度上的影响。为了研究样本个数对2种分布拟合精度的影响，基于Monte-Carlo 方法抽取不同个数的样本，分别利用上述2种分布进行拟合，并根据K-S 检验值与累积概率2 种指标，评判2 种分布的拟合效果。

5.1 模拟样本的生成

以年最大标准风压样本为例，并以α=0.001 5和β=17 602.505 8(即9 602.505 8+8 000)的Gumbel分布函数作为母函数，利用Monte-Carlo 方法生成8 组样本，个数分别为 15，20，30，50，100，200，500 和1 000。表5 所示为模拟样本数据的统计结果(由于生成的模拟数据较多，文中没有给出具体的模拟样本数据)。

5.2 概率分布的拟合优良性检验

以样本个数分别为15，50，200 和1 000 的4组模拟样本为例进行说明，绘制概率分布函数曲线，见图3。从图3 可以看出：不论样本个数较少还是较多，相对于Gumbel 分布曲线，NID 分布曲线和经验分布曲线都更加接近。图3所示概率概率分布曲线还表明：不论样本数据的实际分布完全符合经典分布还是有一定的波动性，正态信息扩散方法均可以很好地刻画样本的实际分布。

参考4.2节的检验对比过程，得出模拟数据的K-S 检验值和累积概率的计算结果，见表6。从表6 可见：对于每一组模拟样本而言，NID 分布和Gumbel 分布均通过了置信水平为95%的临界值检验，但Gumbel 分布的检验结果均大于NID 分布的检验结果，这说明在不同的样本个数下，NID分布的拟合优良性更佳。此外，在截尾区间下，Gumbel 分布的累积概率始终小于1.000 0，但NID分布的累积概率恒等于1.000 0，并不受样本个数变化的影响。

根据表6 绘制模拟样本个数递增下Gumbel 分布与NID 分布的K-S 检验值变化曲线，如图4 所示。从图4 可见：在样本个数递增时，临界值和NID 分布的检验值均逐渐递减并趋于收敛，而Gumbel 分布的检验值在n=20 和n=500 的点附近存在先增后减的情况，即存在一定波动性。

同样，根据表6中的数据绘制模拟样本个数递增下Gumbel 分布与NID 分布的累积概率变化曲线，如图5 所示。由图5 可知：在样本个数递增时，Gumbel 分布的累积概率波动范围较大且毫无规律性，而NID 分布的累积概率始终为1.000 0，与样本个数的变化无关。

6 工程应用：核管道最大腐蚀深度的预测

为了进一步说明正态信息扩散分布推断方法的可行性与有效性，以2个核管道腐蚀深度的预测问题作为工程实例进行对比分析[24-25]。

1)某被腐蚀核管道在一定时间内的平面观测深度实测值分别为2.82，2.96，3.08，3.09，3.18，3.19，3.22，3.32，3.33，3.52，3.58，3.61，3.62，3.95 和4.12 mm。周国强等[26]认为其分布符合极值Ⅱ型分布并预测该核管道最大腐蚀深度为4.840 3 mm。用正态信息扩散分布拟合该组数据并计算相应的K-S 检验值，结果显示：极值Ⅱ型分布的检验结果(即以核管道最大腐蚀深度为变量的检测结果，量纲一参数)为0.115 0，NID分布的检验结果为0.106 4。这2 种分布的检验值均小于临界值0.338 0，显然，上述分布均通过了临界值检验。根据张博庭[27]提出的有限比较法可知，极值Ⅱ型分布的有限比较结果大于NID 分布的有限比较结果，这说明NID分布更适合作为此核管道腐蚀深度的概率分布。以NID 分布作为最大腐蚀深度的预测模型，计算得到该核管道最大腐蚀深度为4.284 9 mm。由此可知：选择拟合效果更好的NID分布作为预测模型，其最大腐蚀深度的预测结果会更加精确。

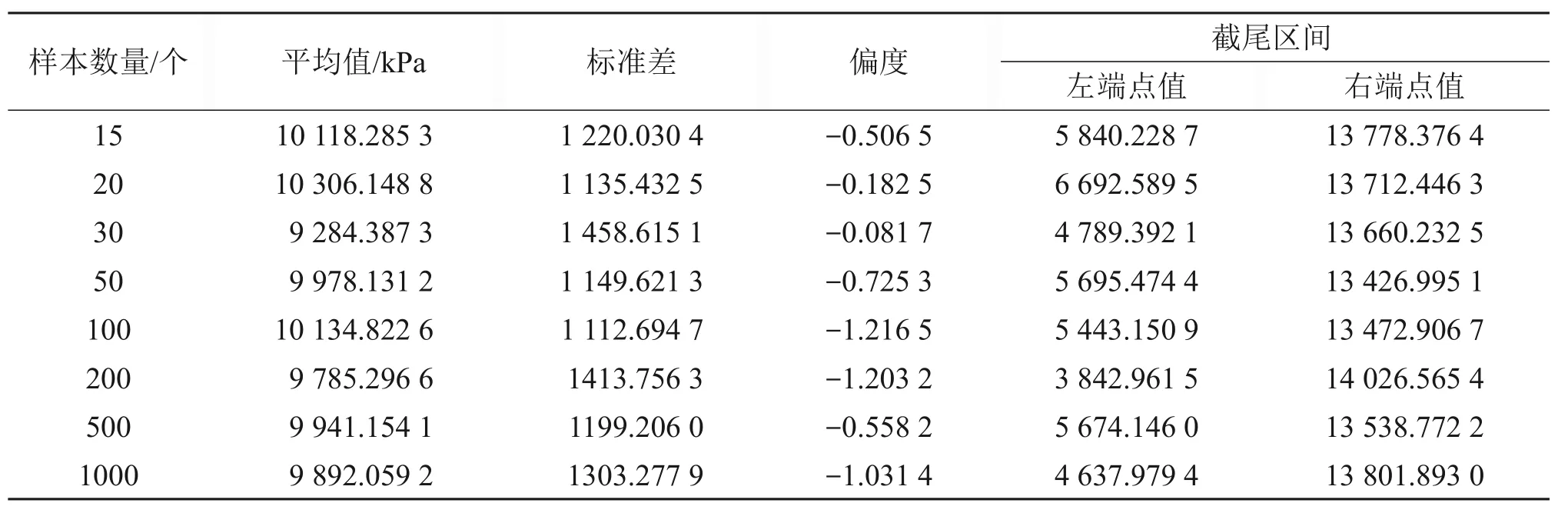
表5 年最大标准风压的模拟数据统计信息Table 5 Statistical information for simulated data of annual maximum standard wind pressure

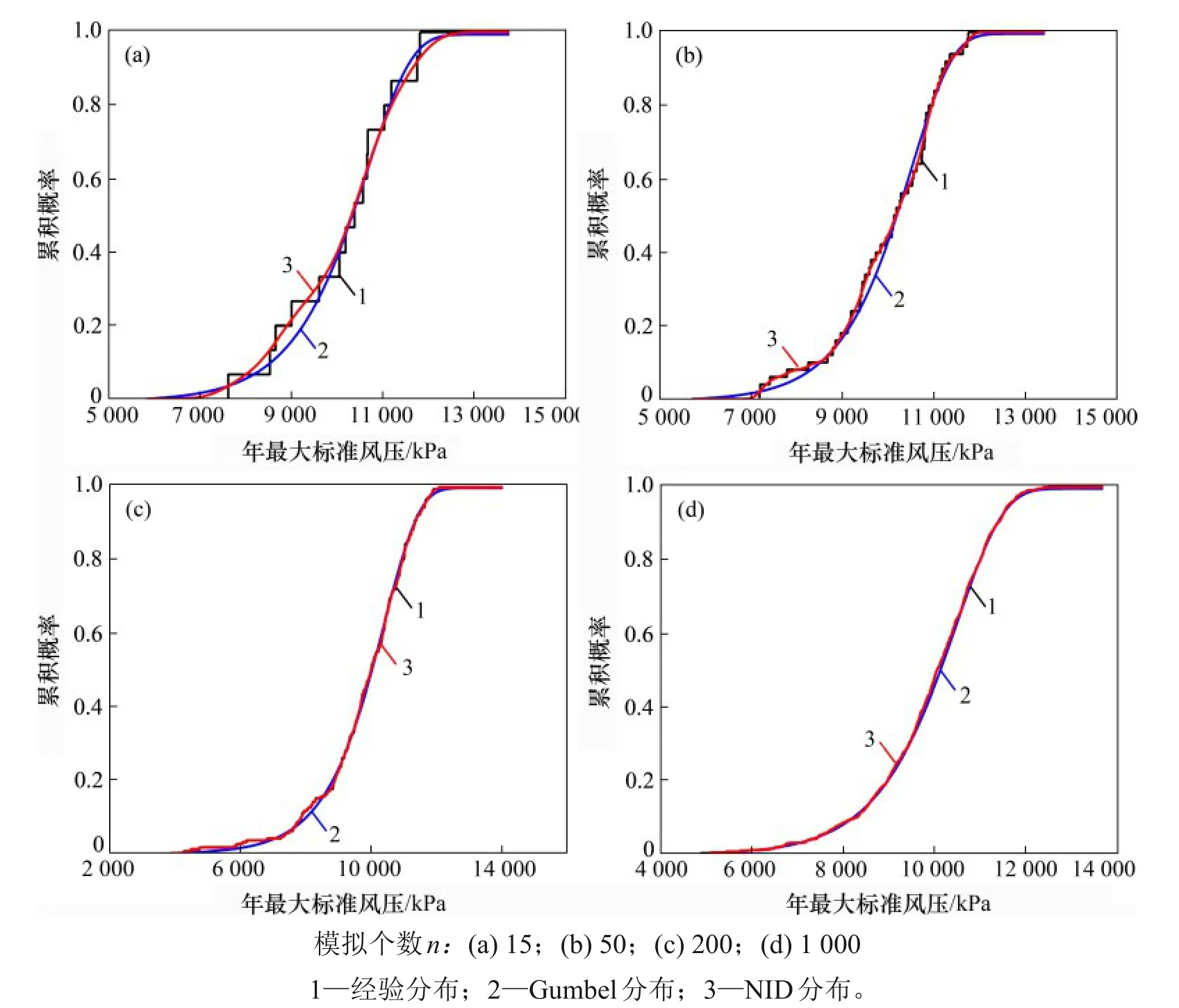
图3 模拟样本的概率分布函数曲线随样本个数增加的比较Fig.3 Comparison of probability distribution function curves for simulated samples with the increase of sample numbers

图4 模拟样本的K-S检验值随样本个数增加的比较Fig.4 Comparison of K-S test values for simulated samples with the increase of sample numbers

图5 模拟样本的累积概率随样本个数增加的比较Fig.5 Comparison of cumulative probability values for simulated samples with increase of sample numbers

为了更加清晰地看出NID 分布的拟合效果，绘制NID 分布和极值Ⅱ型分布的拟合曲线，如图6所示。由图6 可知：极值Ⅱ型分布的累积概率未达到1，而NID 分布的累积概率为1，这说明NID 分布函数能够较好地拟合核管道腐蚀深度的数据点分布。图7 所示为NID 分布与极值Ⅱ型分布的累积概率偏差的变化情况。从图7可明显看出：NID分布的最大偏差小于极值Ⅱ型分布的最大偏差，避免了局部偏差过大的情况，这表明NID 分布能够更好地拟合真实分布；另外，核管道腐蚀深度模型的优化能够更好地提高最大腐蚀深度的预测精度。

图6 实例1的NID分布和极值Ⅱ型分布拟合曲线Fig.6 Fitting curves of NID and extremum Ⅱ-type distributions for example 1

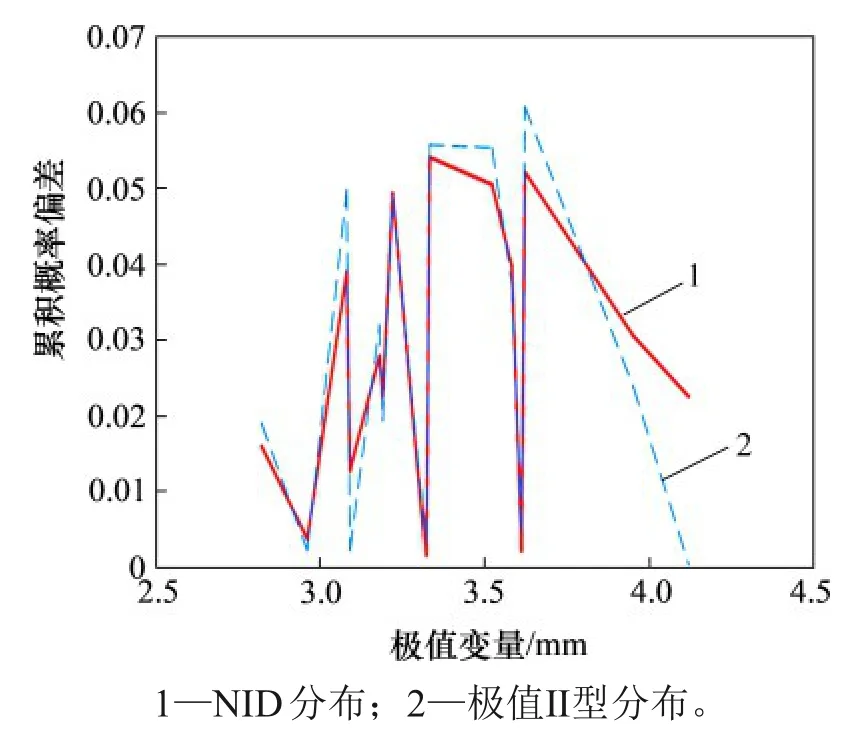
图7 实例1的拟合误差折线Fig.7 Fitting error poly-lines for example 1

2)某核电站设冷水系统除淤管道不锈钢部分运行1 a后的超声测量厚度，在同一条件下，其实测值分别为 2.9，3.7，3.9，3.9，4.6，4.7，4.8，5.0，5.4，5.5，5.7，5.9，6.0，6.3，6.3，7.0 和8.1 mm。周国强等[26]认为其分布符合极值Ⅲ型分布并预测该核管道最大腐蚀深度为9.3 mm。按照实例1 的计算过程，进行K-S 检验值计算，结果显示：极值Ⅲ型分布的管道不锈钢部分腐蚀深度检验结果为0.120 1，NID分布的检验结果为0.085 9。这2 种分布的检验值均小于临界值0.318 0。同理，这2种分布均通过了K-S检验，但极值Ⅲ型分布的有限比较结果大于NID 分布的比较结果。显然，NID分布比极值Ⅲ型分布更适合作为此核管道腐蚀深度的概率分布。利用NID 分布预测该核管道最大腐蚀深度为8.7 mm，表明由极值Ⅲ型分布预测的最大腐蚀深度比NID分布的大。与实例1进行比较可得出同样的结论，即选择拟合效果更好的NID分布作为预测模型，其最大腐蚀深度的预测结果会更加精确。

同理，绘制该样本的NID 分布和极值Ⅲ型分布的拟合曲线图，如图8 所示(其中，极值变量指核管道最大腐蚀深度)。由图8 可知：核管道腐蚀深度样本数据点大致分布在NID分布曲线的两侧，表明NID分布有较好的拟合效果。图9所示为该样本的拟合误差折线图。从图9可知：极值Ⅲ型分布的最大偏差大于NID 分布的最大偏差，说明NID分布更加接近真实分布。

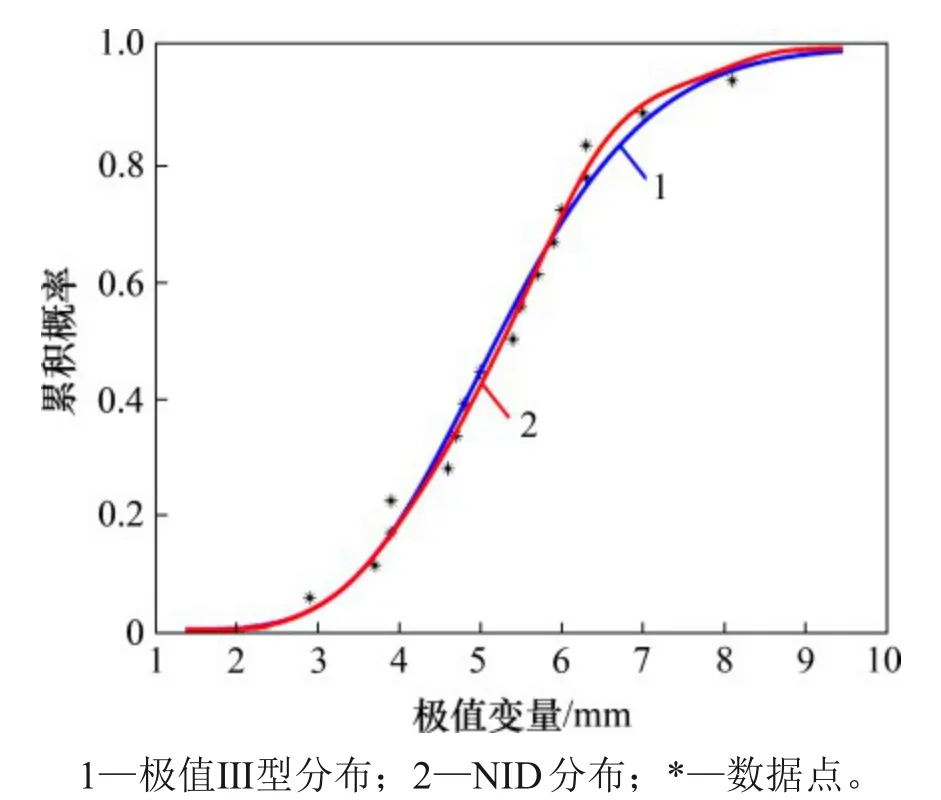
图8 实例2的NID分布和极值Ⅲ型分布拟合曲线Fig.8 Fitting curves of NID and extremum Ⅲ-type distributions for example 2

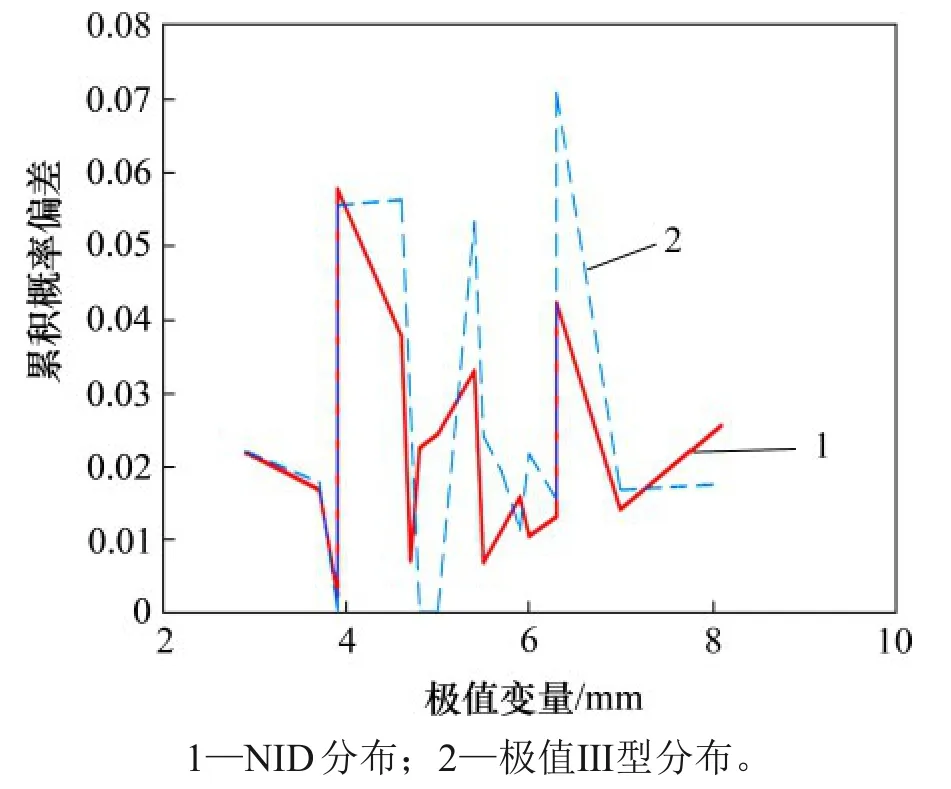
图9 实例2的拟合误差折线Fig.9 Fitting error poly-lines for example 2

7 结论

1)利用正态信息扩散分布和极值型分布分别对年最大标准风压和内摩擦角2组工程样本进行拟合，正态信息扩散分布的K-S 检验值比极值Ⅰ型(Gumbel)分布的K-S检验值小；正态信息扩散分布的累积概率等于1，而Gumbel 分布的累积概率小于1。正态信息扩散分布的曲线能够更好地反映真实样本的直方图或经验分布折线的波动变化。

2)在不同样本个数下，正态信息扩散分布与Gumbel 分布均通过了K-S 检验，但正态信息扩散分布的检验值均低于Gumbel 分布的检验值。随着样本个数增加，正态信息扩散分布的K-S检验结果具有更快的收敛速度和更好的收敛稳定性；正态信息扩散分布的累积概率始终等于1，并不受样本个数的影响，而Gumbel 分布的累积概率有较大的波动范围并恒小于1。

3)正态信息扩散分布预测模型比极值Ⅱ型分布或极值Ⅲ型分布的模型精度更高；由正态信息扩散分布预测的最大腐蚀深度比极值Ⅱ型分布或极值Ⅲ型分布的预测结果更加精确。

4)正态信息扩散方法在推断极值型工程参数的概率密度函数方面具有分布参数唯一、计算过程简便、累积概率恒定、拟合检验值低、对样本个数适应性强的特点。