基于节点蓄意攻击的因特网鲁棒性研究

杨 泉，丁 琳

(南华大学计算机学院，湖南 衡阳 421001)

0 引 言

近年来，复杂网络的鲁棒性问题引起了许多学者的极大关注，特别是，许多研究人员致力于级联故障的研究，这已经成为网络安全中最重要的主题之一。级联故障是一种连续故障，通常由一个或几个节点的随机故障或蓄意攻击触发，并最终导致整个网络严重受损。在现实生活中，级联故障多发生于基础设施网络，并经常引发各种灾难性事件，造成严重的经济损失。例如，一些国家的大规模停电[1-3]、一些大城市频繁的交通瘫痪和互联网崩溃[4-5]等。因此，对于现实网络抵制级联故障的鲁棒性研究变得越来越重要。

为了减少或预防级联故障的发生，许多研究者从不同的角度对级联现象进行了研究，得出了许多有价值的结论，主要集中在级联故障的各种建模方法[6-9]、级联机制和控制措施[10-12]、保护和攻击策略[13-15]、相依网络的级联建模[16-18]等。在以往的级联故障研究中，一个关键的问题是如何给节点或边分配初始负载。在早期的研究中，节点或边的初始负载通常定义为该节点或边的介数。应用介数，Motter等人[19]的开创性工作讨论了复杂网络上基于级联的攻击，并验证了对单个重要节点(高负载节点之一)的攻击可以触发大规模级联故障。此后，为了更好地控制和防御复杂网络中的级联故障，基于介数方法，Motter[10]引入并研究了一种无成本的防御策略，该策略在初始攻击或故障之后，基于有选择地进一步移除节点和边，并发现有意移除网络元素可以大幅度减小级联的大小。Crucitti等人[20]提出了一种基于网络上流的动态重新分配的简单级联故障模型，并且表明单个节点(高负载节点之一)的故障足以使整个系统崩溃。虽然在许多实际情况下，通过介数定义节点或边的初始负载能够很好地反映物理量的流动，但对于某些大规模的现实网络而言，这可能是不切实际的，因为介数考虑了网络的全局拓扑信息，而大规模网络的全局拓扑信息是很难获取的。因此，考虑到局部度的简单性以及网络权重，基于由边连接的2个节点的度的信息，Wang和Chen[6]提出了一种新的定义边的初始负载的方法，并提出了一个加权流局域重分配的级联模型。通过分析加权网络上的级联现象，他们发现当模型中的权重参数为1时，网络达到最强鲁棒性。在他们的工作的推动下，许多研究者从度的角度定义节点或边的初始负载，构造了不同的级联模型并应用到现实网络中。如，Wang等人[21]应用加权流重分配的级联模型研究了美国西部电网在2种攻击下对级联故障的响应，发现模型参数对网络的鲁棒性有着不同影响；Luo等人[22]应用局域负载重分配的级联模型分析了复杂电网上的级联故障，研究表明，与传统网络上的研究结果相比，电网在模型参数为1时并没有达到最强鲁棒性，而是模型参数越大，电网的鲁棒性越强。

然而，现有研究大多是关注电网或通用理论复杂网络的级联故障动态行为及其鲁棒性，而对通信网络的动态鲁棒性研究仍然相对较少。因此，本文考虑实际的因特网，使用节点度的函数形式表示节点初始负载，并基于故障节点的负载局域重分配原则，构建一个具有可调参数的级联故障模型，探讨因特网在蓄意攻击下的鲁棒性，并研究网络参数对因特网鲁棒性的影响。为更好地理解不同节点在级联故障中的作用，本文采用2种不同的攻击策略，即以降序方式来攻击网络中负载最大的节点和以升序方式来攻击网络中负载最小的节点。通过数值模拟，发现级联故障模型中的可调负载参数对受到攻击后的网络鲁棒性有着重要影响。

1 因特网级联故障模型

本文将因特网拓扑抽象成一个具有N个节点和E条边的无权无向的简单图，记为G=(V,M)。其中，V代表所有节点(顶点)的集合，M则代表所有边(链路)的集合。并定义一个N×N的邻接矩阵[aij]来表示节点之间关系，如果aij=1，表示节点i与节点j之间有边直接相连；如果aij=0，则没有直接相连的边。

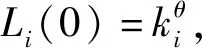
Ci=(1+α)Li(0)

(1)

Ci=αLi(0)+β

(2)

其中，α≥0和β≥0为控制节点容量的可调参数。

当因特网中的节点受到攻击时，该节点会发生故障并立即被网络删除，被攻击节点的负载将被重新分配给其他节点。而在故障节点负载的重新分配过程中，采用不同的分配方式将对网络的级联故障过程有着不同程度的影响。

在以往复杂网络的级联故障研究中，节点负载的重新分配有2种，一种是将故障节点负载分配给网络中其他节点的全局负载重分配策略；另一种是将故障节点负载分配给其相邻节点的局域负载重分配策略。

考虑到负载的重新分配是一个瞬时行为，故障节点的负载必须通过其相邻节点，因而故障节点的邻居节点将受到最严重的影响。因此，本文采用局域负载重分配策略，它分为2种情况：

1)将故障节点的负载按其邻居节点的初始负载比例分配到该节点的所有邻居节点。如果节点i发生故障了，则它的邻居节点j接收的负载比例为：

(3)

其中，Γi为节点i的邻居节点集合。

2)将故障节点的负载根据其邻居节点的剩余容量比例来分配给该节点的所有邻居节点。如果节点i发生故障，其邻居节点j所接收到的负载比重为：

(4)

其中，Lj表示节点j的负载。

由于级联故障的传播过程非常快，依据公式(4)的分配原则，需要不断与故障节点的邻居节点交换当前的剩余容量信息，这可能会加剧网络的崩溃。因此，本文简化负载分配方式，采用公式(3)来分配故障节点的负载。于是，故障节点i的邻居节点j所接收到的负载为：

(5)

如果节点j的总负载超过其容量，即Lj+ΔLji>Cj，则节点j会发生故障，其负载会根据公式(5)重新分配给它的邻居节点，这可能会触发更多的节点故障。当网络中所有节点的负载都不超过其容量时，级联故障才会终止。

在级联故障结束后，为了量化级联故障产生的破坏，本文采用归一化雪崩规模来表示网络的鲁棒性，即：

(6)

其中，Si表示雪崩规模，定义为由移除节点i所导致的故障节点数量，A和NA分别表示攻击节点的集合与数量。

2 攻击策略

在本文的级联模型中，对于一个给定的θ值，当α足够小，即每个节点的容量有限时，任意节点的故障都会导致整个网络的崩溃；而当α足够大，即每个节点都具有较大的额外负载处理能力时，网络不会发生级联故障且保持正常而有效地运行。因此，网络存在一个从崩溃状态逐渐转为正常状态的相变，即关键阈值αc。当α≥αc时，每个节点都具有足够大的容量来处理额外负载，网络不会发生级联故障并且正常运行；而当α<αc时，S迅速从0增长到1，并导致部分或整个网络的崩溃。显然，αc越小，网络抵制级联故障的鲁棒性就越强。

本文的目的是比较不同攻击策略对网络抵制级联故障鲁棒性的影响。因此，在上述的级联模型中采用了2种简单的攻击策略:

1)对具有最低负载的节点的攻击(LL):按照网络中负载的升序来选择节点，然后从具有最低负载的节点开始逐一删除(如果某些节点具有相同的最低负载，将会按顺序删除)。

2)对具有最高负载的节点的攻击(HL):与LL策略相反，这个策略是按照网络中负载的降序来选择节点，然后从具有最高负载的节点开始逐一删除(如果某些节点具有相同的最高负载，将会按顺序删除)。

3 数值仿真

在本文的实验中，考虑了一个具有N=3015和E=5539的AS级因特网(数据来源于http://snap.stanford.edu/)。因为在级联故障建模过程中考虑了2种不同的负载-容量模型，因此，在公式(1)下讨论了2种攻击策略对网络鲁棒性的影响，在公式(2)下研究了初始负载参数和容量参数对网络鲁棒性的影响。

3.1 2种攻击策略对网络鲁棒性的影响

为了对2种攻击进行对比，本文关注于临界阈值αc与级联模型参数之间的关系。而对于每种攻击策略，将分别选择50个节点作为攻击目标，并且每次的模拟结果都是对十多个因特网数据的结果取平均所得。由于级联模型中参数θ的作用，本实验考虑了2种攻击分别在θ≤0.5和θ>0.5这2种情况下对网络鲁棒性的影响。

图1显示了因特网在θ≤0.5时2种攻击策略下的归一化雪崩规模S与容限参数α之间的变化关系。可以看到，当θ≤0.5时，与HL策略相比，LL策略所引发的级联范围更广，对因特网造成的损害更严重。这种现象可以理解，当θ≤0.5时，网络中每个节点的初始负载都比较小，而且度越小的节点，其初始负载越小。由于故障节点的负载被重新分配给它的邻居节点，低负载节点因为其自身度很小，所以它的邻居节点就少，这意味着低负载节点被分配到更多的额外负载，因而需要更大的容量来处理额外负载，否则就会因为过载而发生故障。而高负载节点则相反，高负载节点因为其自身度很大，所以它的邻居节点很多，这意味着高负载节点会被分配到的额外负载就很小，因而只需要很小的容量就能处理掉额外负载而不会发生故障。但前文已表明，节点的容量是由容限参数决定的，容量越大，表示αc越大，则网络的鲁棒性越弱。因此，在这个情况下，LL策略能更有效地破坏因特网。

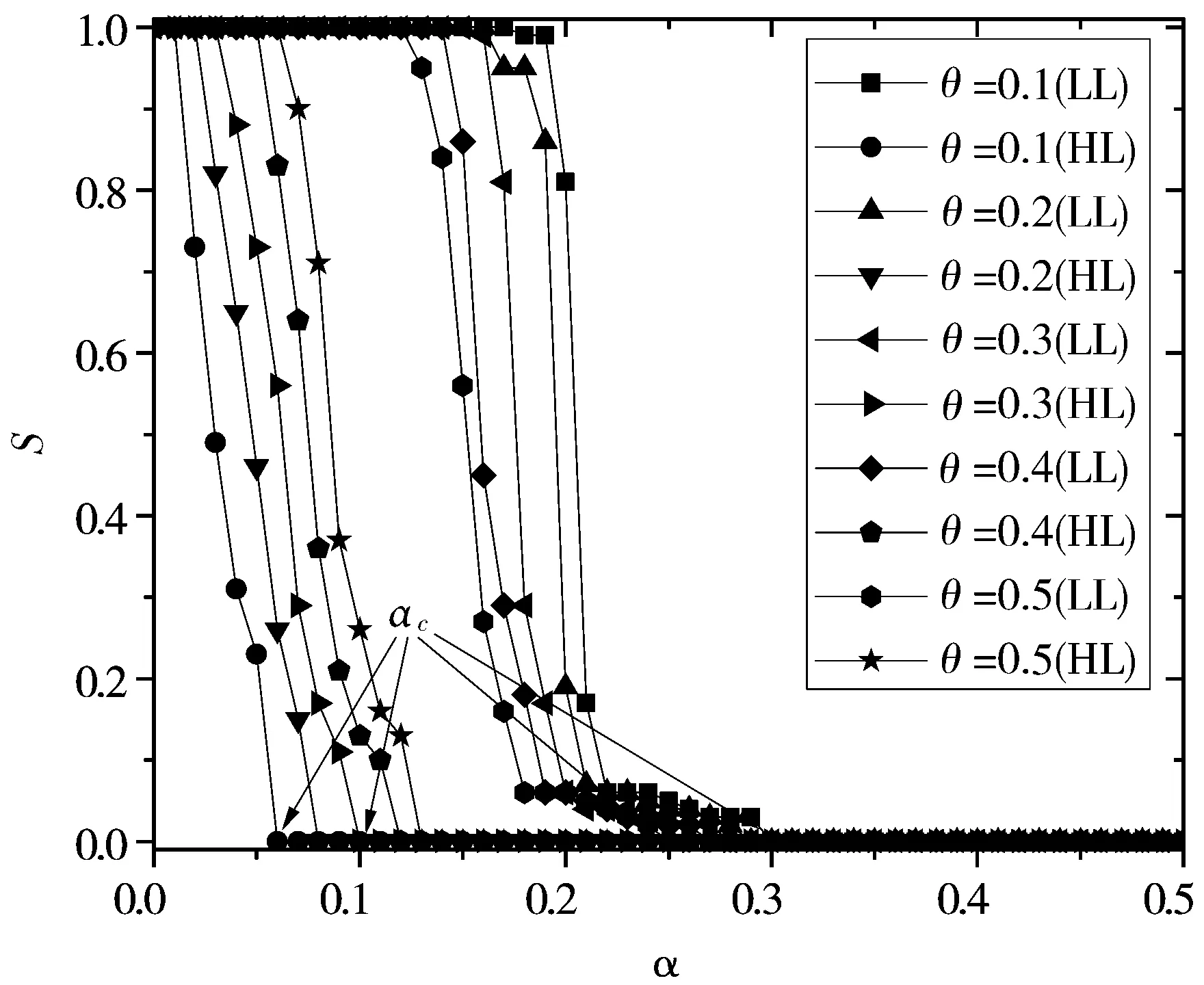
图1 θ≤0.5下的2种攻击策略比较

另外，图1还显示了随着θ的增大，2种攻击策略的影响差异就越小。可以看到，当参数θ的值逐渐从0.1增加至0.5时，LL策略的αc值慢慢变小，即网络的鲁棒性在逐渐增强，这表明在LL策略下，网络的鲁棒性与参数θ成正相关关系；而HL策略的αc值在慢慢增加，即网络的鲁棒性在逐渐减弱，这说明在HL策略下，网络的鲁棒性与参数θ成负相关关系。实验结果具有重要的意义，它可以根据现实网络中的不同情况，为保护有效选择的节点提供指导，以避免级联故障引发的灾难。

图2显示了因特网在θ>0.5时2种攻击策略下的归一化雪崩规模S与容限参数α之间的变化关系。可以看到，图2中存在一个特殊的点，即θ=0.7。当θ=0.7时，2种攻击策略下的αc几乎相同。而当θ>0.7时，HL策略能更有效地破坏因特网。这与之前的美国西部电网在2种不同攻击策略下的研究结果相同，即攻击最高负载节点和攻击最低负载节点[21]。

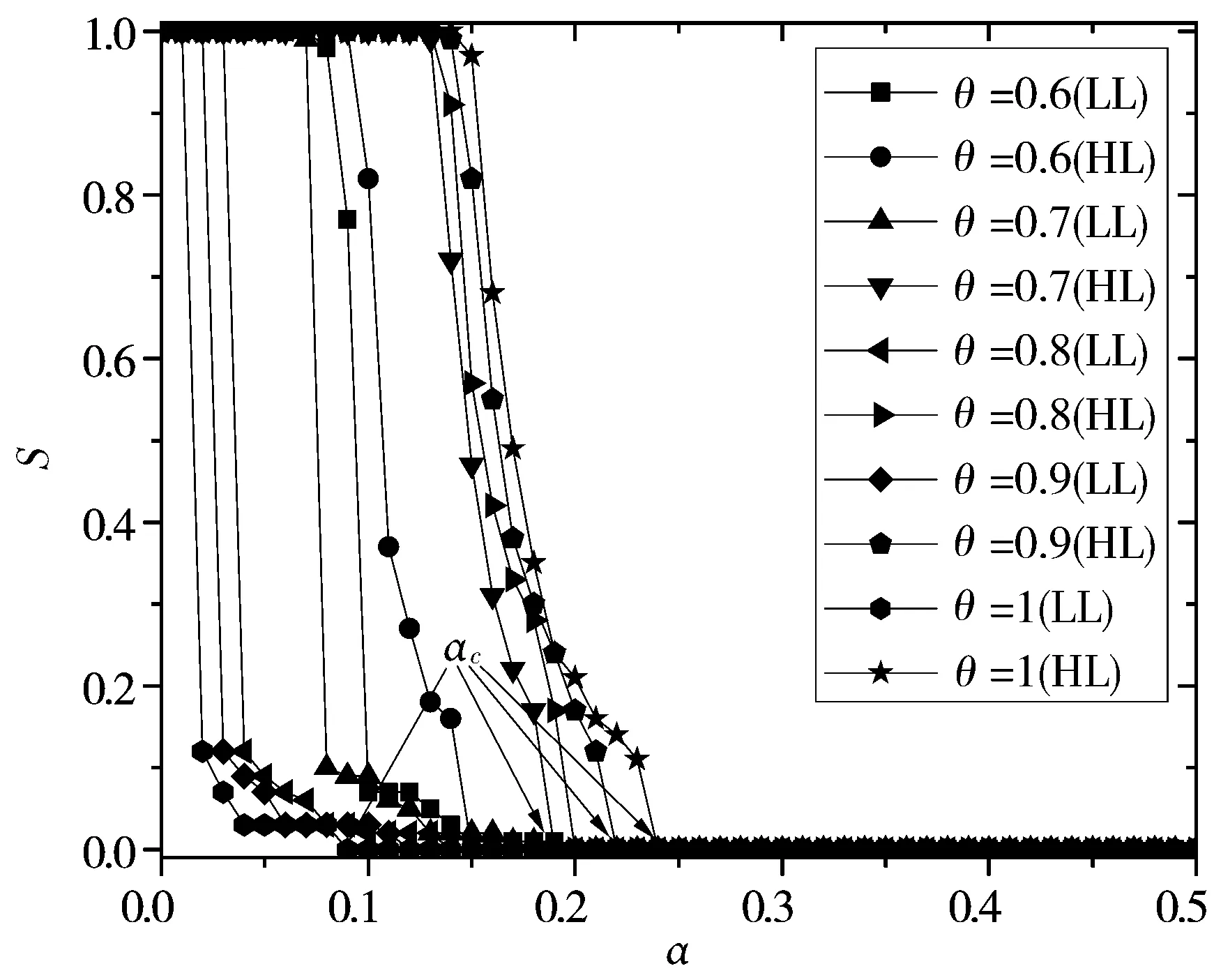
图2 θ>0.5下的2种攻击策略比较

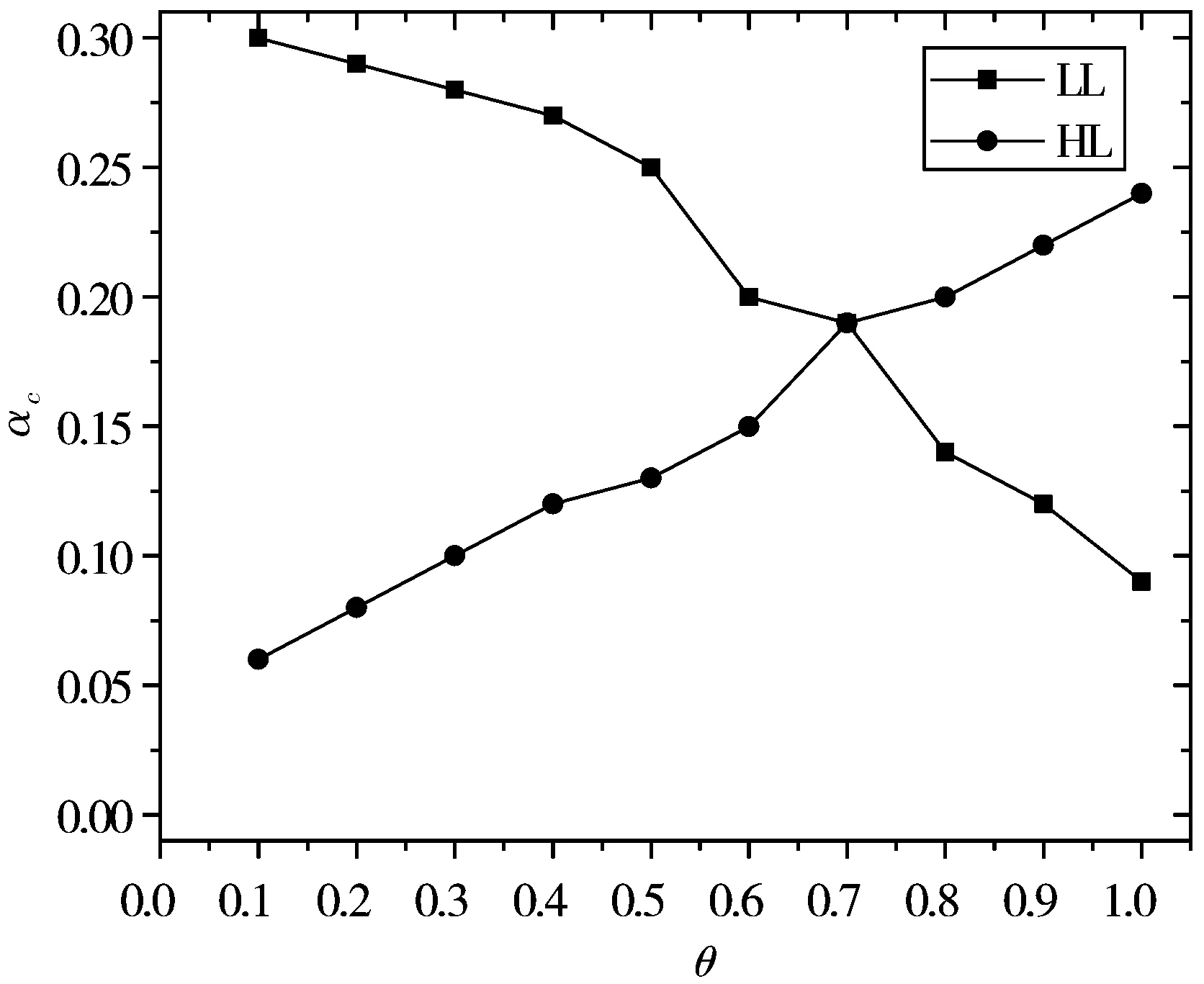
图3 2种攻击策略下的关键阈值αc与参数θ之间关系

此外，本文还进一步地研究了在2种攻击策略下的关键阈值αc与参数θ之间关系，如图3所示。可以直观地看到，在θ=0.7处呈现出2种攻击策略的相互转换。这与之前的很多关于2种不同攻击策略下网络的鲁棒性研究结果一致[21,24-25]，即当初始负载参数达到某一阈值时，2种攻击策略会对网络的鲁棒性产生相同的影响。然而不同的是，文献[24-25]的阈值为0.5，小于本文的0.7。这是因为文献[24-25]中使用的是不相关的无标度网络，并且网络的规模、平均度与实际的因特网也不相同，因而研究结果存在差异性。

3.2 参数对网络鲁棒性的影响

由于攻击策略对网络鲁棒性的影响，本文考虑了初始负载参数与容量参数在LL和HL下对网络鲁棒性的影响。设置β=1，这与以往研究中的研究方法是一致的[23]。与上文相同，对于每种攻击策略，分别选择50个节点作为攻击目标，并且每次的模拟结果都是对十多个因特网数据的结果取平均所得。

图4显示了因特网在攻击最低负载节点下，容限参数α和初始负载参数θ与归一化雪崩规模S之间的关系。从前文可知，0≤S≤1，并且S越小，表示网络的鲁棒性越强。从图4可以看出，α值越小，网络的鲁棒性越弱，当α=0时，无论节点负载如何变化，网络始终处于全崩溃状态。这是由于α值越小，节点所能处理的负载就越小，网络的级联故障就越严重。但随着α值的增加，S值不断减小，并在α=1时(注：这里的α=1是S达到最小时的一个临界值)，网络达到抵制级联故障的最强鲁棒性。

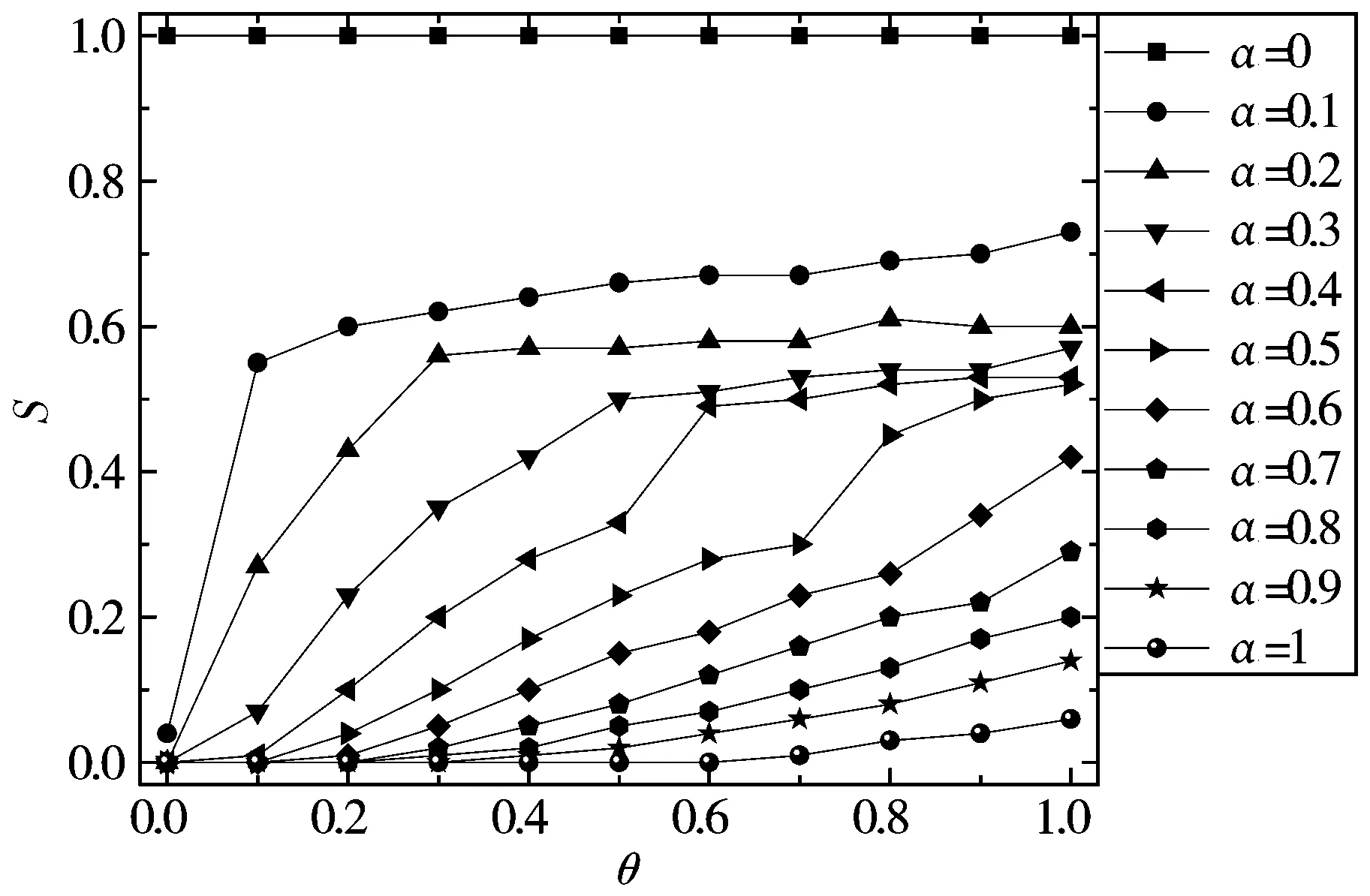
图4 LL攻击策略下,α与θ、S之间关系

另外，图4还显示了随着θ的增加，S也在不断增加。可以看到，当α值为0.1和0.6时，它的S从θ=0时的0.04、0逐渐增加至θ=1时的0.73、0.42，这表示在给定的α下，网络的鲁棒性随着θ的增加而不断减弱，说明节点的初始负载参数与网络的鲁棒性成负相关关系。

图5显示了因特网在攻击最高负载节点下，容限参数α和初始负载参数θ与归一化雪崩规模S之间的关系。从图5可以看出，随着α值的增加，网络的鲁棒性不断增强，并且节点的初始负载参数与网络的鲁棒性成负相关关系。这验证了图4的结论，也说明在LL或者HL策略下，减小节点的初始负载，同时增大节点的容量，能有效控制网络级联故障的发生。

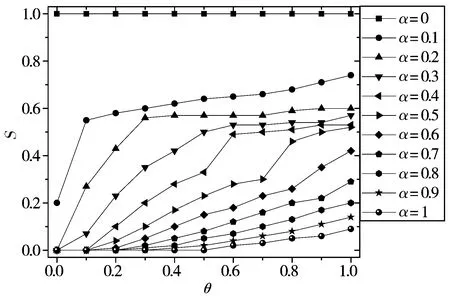
图5 HL攻击策略下，α与θ、S之间关系

4 结束语