车窗三维点云数据修复算法

骆 磊，马荣贵，马 园

(长安大学 信息工程学院，陕西 西安 710064)

0 引 言

三维光学扫描技术能快速获取复杂曲面的点云模型[1-2]，应用广泛。目前车辆轮廓检测主要使用激光扫描技术[3]，其过程为车辆低速通过龙门架，由安装在龙门架两端的测距雷达扫描车辆，获取三维点云数据。由于两端测距雷达水平方向距离车辆较近，并且高度较高，导致激光对车窗扫描时的入射角过大，测量点严重偏离反射面，在车窗处产生特殊噪声点。文中针对这类特殊噪声点，提出车窗三维点云数据修复算法。

对车窗处的点云数据重建有两方面工作，一是去除特殊噪声点，二是点云孔洞修复。在去除特殊噪声点方面，因为这种数据的获取方式现阶段只用来获取车辆的长宽高数据，而特殊噪声点向车体内侧凹陷，不影响数据的检测，所以普遍做法是对特殊噪声点不做处理。因特殊噪声点与正常点有着相似的性质，文中使用点云分割方式去除噪声点，文献[4]中使用谱聚类方法将点云模型过分割，对点云数据有很好的分割效果，但是存在构造相似度矩阵和确定尺度参数σ等问题，不能很好地适应于文中的车辆三维点云数据。文献[5]中采用主成分分析法和局部二次曲面拟合法对点云模型进行微分几何信息估算，并利用双阈值检测方法对散乱点云的特征信息进行提取，该算法可以将特殊噪声点分割出来，但是需要确定阈值。文中提出使用聚类算法确定阈值，并用拟合方式分割特殊噪声点。在点云空洞修复方面，已有很多算法[6-12]，文献[11]中提出一种基于八邻域深度差的算法提取点云孔洞边界，但点云数据的获取方式会导致车辆的三维点云数据上下疏密程度不同，不能有效提取出车窗边界。文献[12]中提出了一种基于SFM的三维点云孔洞修补算法，可以准确地恢复复杂曲面形状，但是需要较高精度的SFM数据集。文献[13]中提出了一种基于径向基函数的孔洞修补算法，该算法对复杂曲面有很好的修补效果。文中对八邻域深度差算法进行改进，提取边界，用径向基函数重建车窗数据。

综上所述，文中根据文献[4-5]提出结合聚类算法和曲面拟合的方法去除特殊噪声点，根据文献[11]提出改进的八邻域深度差方法提取车窗边界，根据文献[12-13]使用基于径向基函数的方式对车窗进行数据修复。主要创新部分在于结合了聚类算法和曲面拟合的方法去除特殊噪声点，并改进了八邻域深度差方法提取车窗边界。具体流程如图1所示。

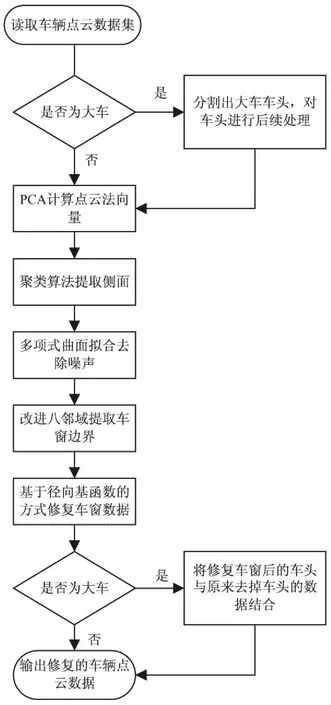
图1 车窗点云数据修复流程

1 相关数据说明

文中采用在龙门架装载测距雷达的方式，对通过的车辆进行扫描，获得点云数据。雷达测距数据经过初步提取，去噪，获得车辆点云数据，记点云数据集合为P，其中x轴方向为车辆宽度方向，车辆的最右端为0，最左端为最大值；y轴方向为车辆长度方向，车辆的最前端为0，最后端为最大值；z轴方向为车辆高度方向，车辆的最低点为0，最顶点为最大值；坐标系原点为车辆的右前底点，其中所有数据的单位均为cm。这里以图2所示的面包车为例，可以看出车窗处有许多噪声点，紧邻着车窗分布，另外点云数据由上到下，成密度由稠密逐渐变稀疏：

图2 汽车三维点云图

2 车窗数据修复

2.1 计算数据点法矢

车辆的点云数据信息量较小，只有三维坐标信息，为后续对点云数据进行处理，丰富点云数据的信息，对数据点进行法矢计算，这里用PCA(principal component analysis)算法[9-13]计算数据点的法矢。

PCA即主成分分析法，用来计算点云数据的法矢。对于道路的点云数据集合P，由于它是无序的，所以在对集合P进行处理之前，需要为其建立拓扑关系，文中使用k-d树(k-dimensional树的简称)[14-16]数据结构建立点云之间的拓扑关系。之后用PCA计算法矢，计算方式如下：

设集合P中的点pi的k邻域点集为Nk(pi)，构造关于点pi的3×3协方差矩阵，如式(1)所示：

(1)

其中，p为数据点pi及其k邻域所构成集合的质心，矩阵C表示点集Nk(pi)的点的分布情况，即邻域点与质心点p的偏离程度。矩阵C为对称半正定矩阵，所以有3个非负实数特征值，设为λ0,λ1,λ2，且λ0≤λ1≤λ2，其对应的特征向量分别为v0，v1，v2。最小特征值λ0对应的特征向量v0即可近似为点pi的法矢ni。

2.2 去除特殊噪声点

对含有特殊噪声点的车窗单独进行处理，为更加清晰地说明特殊噪声点，这里将车辆侧面与特殊噪声点分割出来，如图3(a)所示，其横坐标为车辆三维数据的y轴，其纵坐标为车辆三维数据的z轴，通过侧视图可以看到车窗下方的点云密度较大，是因为本应在车窗处的点由于光学原因，投射到车窗下方。通过车侧面的正视图如图3(b)所示，灰圈中的点云数据即为特殊噪声点，这类噪声点很多，而且连续，如果不去除非常影响车辆三维重建，具体的噪声点形式可以通过车辆点云数据的一个断面进行展示，结果如图3(c)所示，两个灰圈中的点则为前面叙述中的特殊噪声点，呈现向内侧下方凹陷的形状，其距离车辆侧面间隔一小段距离，文中利用这一点，使用聚类提取，拟合曲面的方法，将车辆侧面与特殊噪声点分割开来。

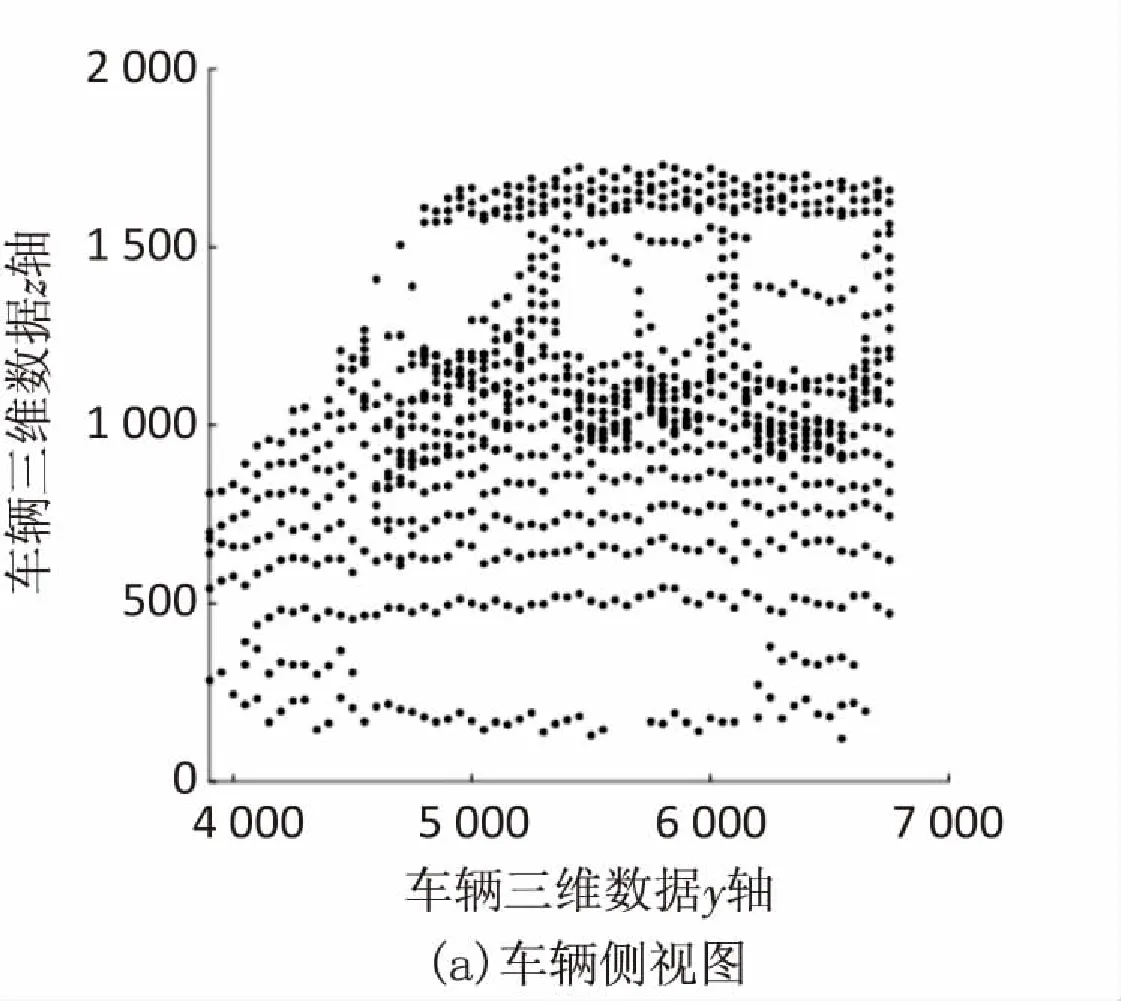
图3 车窗处噪声点说明图

通常情况下，大货车、钩车以及半挂等大型车辆，不像小车整体都有车窗，而是仅车头部分有车窗，所以在进行数据处理的时候，像小车这样前中后都有车窗的车辆，对其整体进行处理，而特殊大型车辆仅处理车头部分。聚类算法可以很好地将拥有同一类特性的点进行提取，经过分析，车辆侧面拥有相近的x值和相近的法矢，利用x值和法矢即可聚类提取车辆侧面。进一步，对于车辆侧面，如图3(b)所示，为中间向外微凸的拱形，因为斜向上的法矢和斜向下的法矢之间的差异会比较大，所以仅仅使用法矢不能将整个侧面提取[17-21]，但是这类差异又不是希望考虑的，又因为车辆侧面与其他面相比法矢的x方向差异最为明显，所以仅用法矢的x方向作为聚类时的数据即可。记车辆点云数据的x值为聚类数据集合的u值，法矢的x方向的值为聚类数据集合的v值，即集合Qcluster={(u,v)|u∈P,v∈n}。另外因为x信息与法矢的信息比例不同，所以要对x数据进行归一化，将范围限定在0到1，则u值的计算公式如式(2)所示：

(2)

其中，X为点云所有x方向数据的集合，x为集合X中的一个值。得到标准化的数据集合Qcluster后，使用多滑动窗口的均值漂移算法[22-24]确定中心点，其算法如下：

(1)在集合Qcluster中随机选取n个点作为初始中心点C1,C2,…,Cn，其半径为r的圆球作为滑动窗口。

(3)计算密度变化量与新密度的比值，如果小于额定值则认为没有变化，执行步骤4，否则再执行步骤2。

(4)将所有的窗口作比较，选择出密度最大的不重叠窗口，将其中心点作为结果。

因为对数据进行了归一化，所以滑动窗口的半径可以确定下来，半径r的取值越大则对车辆侧面数据的要求越宽泛，越小则越严格。文中r依据数据点的分布密度来确定，即数据点到距离其最近的四个点的距离来确定r值，公式如式(3)所示：

(3)

其中，X为点云数据中所有x值的集合，Di为数据点pi的最近邻4个点距离的集合。

对中心点数量的选取，过小则有可能无法确定到真正的高密度中心，过大则影响计算速度。通常情况下n取6到10就可以将密度最大的中心点确定下来，这里为了使结果准确稳定，取n=10。通过确定的聚类中心，可以得到车辆侧面的数据范围，其中Umax表示车辆侧面数据的x值上限，Umin表示车辆侧面数据的x值下限，Vmax表示道路数据法矢的x值上限，Vmin表示道路数据法矢的x值下限，计算公式如式(4)所示：

其中，r即为式(4)中确定的聚类窗口半径，利用上述约束条件，对车辆点云数据进行约束，提取出车辆侧面的数据信息。

但是通过聚类算法提取出的只是部分车辆侧面数据，仍有一些点受噪声干扰，其法矢的方向并不同于大部分点，所以不会被聚类算法提取，这里使用曲面拟合的方式，对现有的准确的车辆侧面点云数据进行数据拟合。曲面拟合[25-27]既可以将车辆侧面全部提取出来，也可以避免一些噪声点的干扰。根据实际观察，所有车辆侧面在竖直方向都有一定的弯曲，而水平方向基本较小，所以，这里做拟合函数x=f(y,z)，其中y、z均为2次拟合，此时R-square=0.873 7，拟合效果符合要求，如果再向上增加拟合次数，不仅R-square增长较小，而且有可能会出现过拟合情况，所以选用x与y均为2次的曲面拟合。为确认曲面拟合的效果，对多种车辆侧面进行曲面拟合，其拟合结果如表1所示。

表1 车辆侧面拟合效果对比

使用曲面拟合的方式对车窗进行修复，为验证曲面拟合的可行性，拟合的效果用R-square和RMSE作为判断标准，则四种车辆侧面的拟合效果如表1所示。从表1可以看出，四种车辆左右侧面拟合的R-square均大于0.8，而左右侧面拟合的RMSE均小于20 mm，说明使用的拟合函数可以很好地对车辆侧面进行拟合，且误差较小。

图4 车窗处噪声点说明图

利用拟合出的曲面，对车辆点云数据进行处理，同样以面包车为例，得到如图4所示的车辆侧面。如图4(a)所示，灰色的点为噪声点，黑色的点为车辆侧面的点，利用曲面拟合的方式，不仅能够把车窗处的噪声点去除，而且能够把在提取车辆数据时，掺入的地面点去除，去除效果如图4(b)所示，可以看出，车辆侧面效果很好，车窗处特殊噪声点都已经去除了。

2.3 提取车窗边界

8邻域深度差的方式在提取车窗边界时存在两个问题，因为车辆的点云数据由左右两侧龙门架上的测距雷达扫描获取，所以点云数据由上到下的疏密程度是不一样的，简单地使用8邻域深度差的话，会将密度稀疏的点云数据作为孔洞边界提取，所以这里需要将8邻域深度差算法进行改进。

改进的八邻域深度差算法首先对点云沿深度方向进行垂直投影，即对三维点云数据的yoz平面投影，对投影点进行栅格数据组织，统计投影点坐标的最大最小值ymin,ymax,zmin,zmax，根据栅格的划分次数m，计算每个栅格的大小为a*b，其中a，b的计算公式如式(5)、式(6)所示：

(5)

(6)

将各投影点分配到各个栅格并且对其进行编号:首先利用当前投影点的坐标(y,z)和栅格的大小a、b计算该点所在栅格的行r和列c，记该点所在栅格的编号为G(r,c)，其中r,c的计算公式如式(7)、式(8)所示:

(7)

(8)

对于任意栅格G(i,j)，统计栅格内投影点的数目，若投影点数目为零，则将该栅格的深度值设定为h=0;若栅格内投影点数目大于0，则将该栅格的深度设定为h=1。对于任意深度值不为0的栅格G(i,j)，计算其8邻域的深度值与其延伸方向的深度值的和s，如果存在结果s为0，则说明该栅格为边缘栅格，反之则不是。其中s的计算公式如式(9)所示：

s=h(i+c1,j+c2)+h(i+2c1,j+2c2),c1,c2∈{-1,0,1}

(9)

其中，h(i,j)表示栅格G(i,j)的深度值。

2.4 基于径向基函数的孔洞修复

文中利用孔洞边界点和它的邻域信息，建立基于径向基函数的隐式曲面，空间点云集合Q={q1,q2,…,qn}，分别对应约束值为{h1,h2,…,hn}，如果能构造函数f(r)使得每个点均满足等式F(qi)=hi，那么方程F(qi)=0就可以表示一个隐式曲面。该隐式曲面要求通过的点称为插值约束点，而不要求通过的点称为附件约束点，这里以车窗边界点及车窗边界点的5个邻域车窗点作为插值约束点，记为Q={q1,q2,…,qn}，在插值约束点处沿插值约束点的法矢方向0.3长度处，计算附加约束点Q={qn+1,qn+2,…,q2n}，则表达式如式(10)、式(11)所示：

F(qi)=hi=0,i=1,2,…,n

(10)

F(qi)=hi(i=n+1,n+2,…,2n)(取hi=1)

(11)

结合式(10)、式(11)构建基于径向基函数的隐式曲面：

(12)

其中，qj表示建立曲面所需的采样点，r表示建立曲面时通过的任意散乱点，ωi为对应每个采样点的权值，P(r)表示P(r)=p0+p1x+p2y+p3z,φ(r-qi)的径向基函数，一般情况下，在对空间散乱点进行插值时经常用的基函数形式φ(r)=|r|3。对于三维空间中的任意两个散乱点，表达式如式(13)所示：

φ(qi-qj)=|qi-qj|3=((qix-qjx)2+(qiy-qjy)2+(qiz-qjz)2)3/2

(13)

为求解权值和一阶多项式的系数值，除有两类约束点所给定的约束值条件，还需要满足正交条件：

(14)

由此建立线性方程组AX=B。因为稀疏矩阵A是插值约束点和附加约束点的插值条件决定的半正定矩阵，所以该方程有唯一解，X是要求的权值ωi和一阶多项式的稀疏矩阵(p0,p1,p2,p3)，B是约束值为hj的列向量，通过高斯消元法可以求出方程的解。

联立式(12)～式(14)，采用高斯消元法解方程组，求解出插值约束点的权值和一阶多项式的系数，从而到曲面的隐式方程。

(z-qjz)2)3/2+p0+p1x+p2y+p3z

(15)

之后采用梯度下降法对车窗点云数据进行填充，梯度下降法的一半形式为：

R1=R0-γ·F

(16)

3 实验结果分析

对四种车辆车窗重建的效果如图5所示，其中灰色部分为重建后车窗的数据点，黑色部分为车辆的数据点，所在坐标系的单位均为mm。图5(a)为面包车，一个侧面有三个车窗分别为前中后，这里以前车窗为例进行放大，通过放大图可以看到，车窗处已经没有特殊噪声点，且修复效果较好，车窗整体没有空白处，达到车窗重建的目的；图5(b)为半挂，可以看到修复效果较好，只是右上角有小块缺损，因为缺损处有两个点被提取为车窗边界点，所以会以此为边界，而将两个点上面的部分作为车辆点云数据不做处理；图5(c)为小型钩车，对于比较方正的车窗，车窗的修复效果很好；图5(d)为大货车，有两个车窗，两个车窗之间的部分和前方车窗部分，其点云数据部分缺损，但仍不影响车窗数据的重建且修复效果较好。

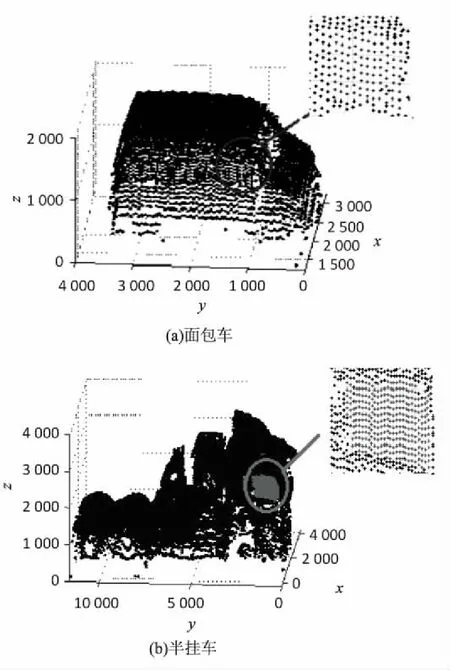
图5 四种车辆车窗修复结果

4 结束语

通过上述实验结果，可以得到结论：聚类算法结合曲面拟合的方法可以很好地去除车窗处由于光学原因产生的特殊噪声点，改进的8邻域算法能够对边界提取有一定的抗干扰能力，基于径向基函数的孔洞修补算法可以很好地重建车窗数据。综上所述，该算法可以对不同类型车辆的车窗进行数据重建，且效果良好。但仍有可以改进之处，比如为提高精度，可以先提取出车窗边框，以车窗周围点作为拟合点，进行曲面拟合去除噪声点，理论上可以提高拟合精度，需要后续进行实验验证。