双向交替折半插入排序法
王代星,袁琳琳
(1.贵州大学 教育教学评估中心、高等教育研究所,贵州 贵阳 550025;2.贵州职业技术学院,贵州 贵阳 550023)
0 引 言
插入排序是计算机内部排序中最简单的排序算法之一。它的基本思想是把第一个元素当作初始有序序列,从第二个元素开始,逐个将所有元素向前插入到该序列之中。插入排序主要有两个基本操作,即查找插入位置时的数据比较和插入时的数据移动,通常把数据比较次数和数据移动次数作为算法的时间复杂度。根据查找插入位置方式的不同,又分为直接插入排序和折半插入排序。折半插入排序也可视为直接插入排序的改进算法,通过折半查找方式,减少了数据比较次数,但数据移动次数没有改变。2-路插入排序[1]是折半插入排序的改进算法,能相对减少排序过程中数据的移动次数,但空间复杂度从O(1)增加到了O(n),时间复杂度受第一个元素影响。当第一个元素是最大或最小的元素时,算法的时间复杂度变得与折半插入排序一致。针对这些不足,文中提出一种改进算法,即双向交替折半插入排序算法。通过在待排序序列的两端交替地插入排序,使数据移动次数比折半插入排序降低了50%、比2-路插入排序降低了25%,避免了2-路插入排序效率受分界元素影响的缺点,排序在序列的中间点结束,空间复杂度恢复为O(1)。
1 2-路插入排序算法简介
对于长度为n的待排序序列r[0…n-1],另设置等长的同类型数组d,将r[0]赋给d[0],将数组d视为一个循环向量,排序在d中进行。将d[0]视作有序序列的中间元素,从r[1]开始,逐个将r中的元素插入到d中。具体插入方法是:对于待插元素r[i],若r[i] 图1 2-路插入排序示例 文献[2]提出了一种名为“双向插入排序法”的改进算法。其基本思想是:对于长度为n的待排序序列r[0…n-1],排序在两端进行。取r[0]、r[n/2]、r[n-1]三个元素中大小在中间的元素为分界元素,分别从右向左扫描和从左向右扫描待排序序列。在从右向左扫描时,将不小于分界元素的元素,向右侧有序序列插入;当遇到小于分界元素的元素时,停止向左扫描,将该元素插入左侧有序序列,然后开始从左向右扫描。在从左向右扫描时,将不大于分界元素的元素,向左侧有序序列插入,当遇到大于分界元素的元素时,停止向右扫描,将该元素插入右侧有序序列,然后又开始从右向左扫描。如此交替扫描和插入,直到处理完所有待排序元素为止。 双向插入排序法优于2-路排序法,空间复杂度为O(1),最终排序结果顺序存储在原序列中。但使用分界元素的不足之处仍未能避免。当分界元素碰巧为待排序序列的最大、最小,或次最大、次最小时,算法退化为单路插入,排序效率跟折半插入排序一致。与文献[2]类似的还有文献[3-5]提出的算法。 文献[6]提出了“循环插入排序法”。其算法的基本思想是:对于长度为n的待排序序列r[0…n-1],把r[n/2]元素作为初始有序序列,即把有序序列安排在整个序列的中部,待排序元素两侧,插入在中部有序序列的两端循环进行。设置两个指针,分别指向中部有序序列的低端和高端。扫描待排序元素,当待排序元素大于有序序列中间的元素时,在有序序列的高端插入,高端指针向右移动加1;否则,在有序序列的低端插入,低端指针向左移动减1。直到所有持排序元素扫描结束为止。该算法的优点是每次数据移动的次数都不大于有序序列长度的一半,能够有效减少数据的移动次数。但美中不足的是在排序过程指针越界时,要作循环处理;排序结束后,需要重新整理移动数据,需要1到n/2个数量不等的元素辅助空间。文献[7-8]与文献[6]的思路完全一样,只是有序序列安排在循环序列的两端。 文献[9]提出了“一种新的2路插入排序算法”,排序在序列的两端进行,待排序元素先与后端的最小元素比较,若大,则在后端插入;反之,则在前端插入。 其他的多路插入排序算法,有的增加了空间复杂度,有的增加了数据的比较次数,有的设置了一个或多个分界元素,比如文献[10-16]等,此处不再详述。 在没有特别说明或不影响理解的情况下,算法即指双向交替折半插入排序算法。 以数据非递减排序为例。对于给定长度为n的待排序序列r[0…n-1],为不增加辅助空间,排序在原序列中进行,即原地排序;为有效减少数据移动次数,保证数据最终按非递减排列,先在序列的左右两端按非递减排序,再逐渐向中间靠拢,同时保证右端有序序列的数据不小于左端有序序列的数据;为让大的数据尽早向右移,让小的数据尽早向左移,在扫描待排序数据时,采取从右向左和从左向右双向交替扫描的方式,分别将大的数据插入右部有序序列和将小的数据插入左部有序序列,保证左右两端的有序序列等长,排序最终在序列的中间点结束;在排序过程中,既要随时保证右端有序序列数据不小于左端有序序列数据,同时也要充分利用这一特性,减少数据的比较和移动次数。在两端有序序列中插入元素时,采用折半插入法,以减少数据的比较次数。 具体做法如下:初始化左右两端有序序列,比较r[0]与r[n-1],若r[0]>r[n-1],则交换r[0]与r[n-1],保证左端的初始有序序列不大于右端的初始有序序列。设置两个指针left与right,分别指向左端有序序列的最后一个元素和右端有序序列的第一个元素。初始时,left=0,right=n-1。首先,从右端向左端扫描,比较r[right-1]与r[right],若r[right-1]>r[right],则r[right-1]向右端插入,指针right减1;若r[right-1] 图2 双向交替折半插入排序示例 算法:双向交替折半插入排序 输入:随机序列r[0…n-1] 输出:非递减序列r[0…n-1] 方法: Step1:初始化。若r[0]>r[n-1],则r[0]与r[n-1]交换;左端有序序列指针left=0;右端有序序列指针right=n-1; Step2:从右端向左扫描。若r[right-1]>r[right],则r[right-1]向右端插入,right--;若r[right-1] Step3:从左端向右扫描。若r[left]>r[left+1],则r[left+1]向左端插入,left++;若r[left] Step4:若left Step5:输出r[0…n-1],算法结束。 以下的分析,皆以随机序列为例。 3.3.1 时间复杂度 算法的排序时间主要消耗在数据的比较和移动上。由于计算机硬件环境和程序语言的差别,一般不用绝对运行时间来衡量排序算法的效率,而采用排序过程中所发生的数据比较次数和数据移动次数来衡量。算法的数据比较次数,主要发生在查找数据插入位置时。本算法在排序过程中,把有序序列均等地分布在序列的两端,数据插入在两端进行,减少了后半部分元素在插入有序序列时数据的比较次数,平均每个元素减少了1次,总的比较次数减少了约n/2次。传统折半插入法平均数据比较次数为nlog2n,则本算法的平均数据比较次数不高于nlog2n-n/2。后文的实验数据也证明了这一点。算法的数据移动次数,主要发生在数据插入时。同样,由于数据插入是在两端等长的有序序列中进行,每一端有序序列的长度,都相当于传统的折半插入法排序时的有序序列长度的一半,故平均数据移动次数减半。传统的折半插入法的平均数据移动次数约为n2/4,则本算法的平均数据移动次数约为n2/8。后文的实验数据证明了,本算法的平均数据移动次数比传统的折半插入法下降了50%,比2-路插入法下降了25%。 3.3.2 空间复杂度 从前面的算法分析和算法描述可以得知,本算法只需要一个元素辅助空间,作为数据交换时的临时存储空间,故空间复杂度为O(1)。 3.3.3 算法的稳定性 由于插入排序是在序列的两端交替进行,同时为了保证右端的有序序列不小于左端的有序序列,元素会在两端移动,即序列左半部分的数据,有可能插入到右端的有序序列中,右半部分数据也可能插入到左端有序序列中,因此,算法是不稳定的。 通过实际测试,得出实验数据与结果,其中随机序列的统计数据,是执行了100次的平均数。另外,两数据交换位置,按两次数据移动统计。 表1给出了算法在不同的排序规模和三种主要数据序列状态下进行排序时实际的数据比较次数。当原序列为随机时,比较次数不超过nlog2n-n/2次;正序时,为2n-3次;逆序时,为nlog2n/1.9次。 表1 双向交替折半插入排序法的数据比较次数 表2给出了算法在不同的排序规模和三种主要数据序列状态下进行排序时实际的数据移动次数。当原序列为随机时,移动次数约为n2/8次;正序时,为0次;逆序时,为1.5n次。 表2 双向交替折半插入排序法的数据移动次数 下面比较了直接插入、折半插入、2-路插入和双向交替折半插入排序的实验数据。在图表中,双向交替折半插入排序简称双向交替。实验数据分别按随机、正序和逆序序列,给出数据比较次数和数据移动次数的对比。 4.2.1 对随机序列排序对比 表3给出了4种排序算法数据比较次数的对比。直接插入法的数据比较次数约为n2/4;折半插入、双向交替和2-路插入不超过nlog2n。由于双向交替法需要保证右端有序序列不小于左端有序序列,所以数据比较次数比2-路插入法要约高。通过表中数据计算,平均约高1.6%。 表4给出了4种算法数据移动次数的对比。直接插入和折半插入的数据移动次数是一样的,约为n2/4;2-路插入约为n2/6;双向交替约为n2/8。双向交替比2-路插入约减少了25%。图3显示了数据移动次数随着排序规模变化的趋势图,直接插入与折半插入重叠一致,双向交替增长最缓慢。 表3 对随机序列排序时的数据比较次数对比 表4 对随机序列排序时的数据移动次数对比 图3 随机序列数据移动次数对比 4.2.2 对正序序列排序对比 表5给出了4种排序算法数据比较次数的对比。2-路插入法不仅是4种算法中数据比较次数最多的,而且通过与表3比较,数据比较次数还要约高于在随机序列排序时,同样约为nlog2n次;双向插入为2n-3次;直接插入和折半插入为n-1次。 表5 对正序序列排序时的数据比较次数对比 表6给出了4种算法的数据移动次数的对比。2-路插入法需要移动数据2n次;其他算法无需移动数据。 表6 对正序序列排序时的数据移动次数对比 续表6 4.2.3 对逆序序列排序对比 表7给出了4种排序算法数据比较次数的对比。此时,直接插入的数据比较次数达到最高,约为(n-1)(n+2)/2次;2-路插入和折半插入相近,约为nlog2n次,跟随机序列排序时的比较次数悬殊不大;双向插入比较次数最少,约为nlog2n/1.9次,比2-路插入排序降低了47.37%。 表7 对逆序序列排序时的数据比较次数对比 表8给出了4种算法的数据移动次数的对比。此时,直接插入和折半插入的数据移动次数达到最高,为(n-1)(n+2)/2次;2-路插入为2n次;双向交替约为1.5n次,比2-路插入排序降低了25%。 表8 对逆序序列排序时的数据移动次数对比 通过“3.3 算法分析”和“4 实验数据与结果”得出,文章提出的双向交替折半插入排序法,在对随机序列进行排序时,数据比较次数不超过nlog2n-n/2次,数据移动次数约为n2/8次;在对正序序列进行排序时,比较次数为2n-3次,数据移动次数为0次;在对逆序序列进行排序时,比较次数约为nlog2n/1.9次,数据移动次数约为1.5n。与2-路插入法对比,在对随机序列进行排序时,数据比较次数约增1.6%,数据移动次数约减25%;在对初始序列为正序或逆序序列排序时,也有比2-路插入法良好的表现;空间复杂度为O(1),也比2-路插入法的O(n)少;且在排序时,当第一个元素为序列中最小或最大值的元素时,2-路插入法退化为单路插入,排序效率与折半插入排序一致,而双向交替折半插入排序法则没有这样的缺点。综上所述,双向交替折半插入排序法的综合性能优于2-路插入排序法。 总的来说,2-路插入排序及其改进算法,其数据的移动次数跟直接插入排序法还是一个数量级的,要彻底有所改进,只有改顺序存储结构为链式存储结构,比如文献[17]所述算法,但数据的比较次数又难以兼顾。实际应用应综合考虑数据比较和移动的代价。
2 具有代表性的其他改进算法
2.1 有分界元素的改进算法
2.2 无分界元素的改进算法
3 双向交替折半插入排序
3.1 算法思想
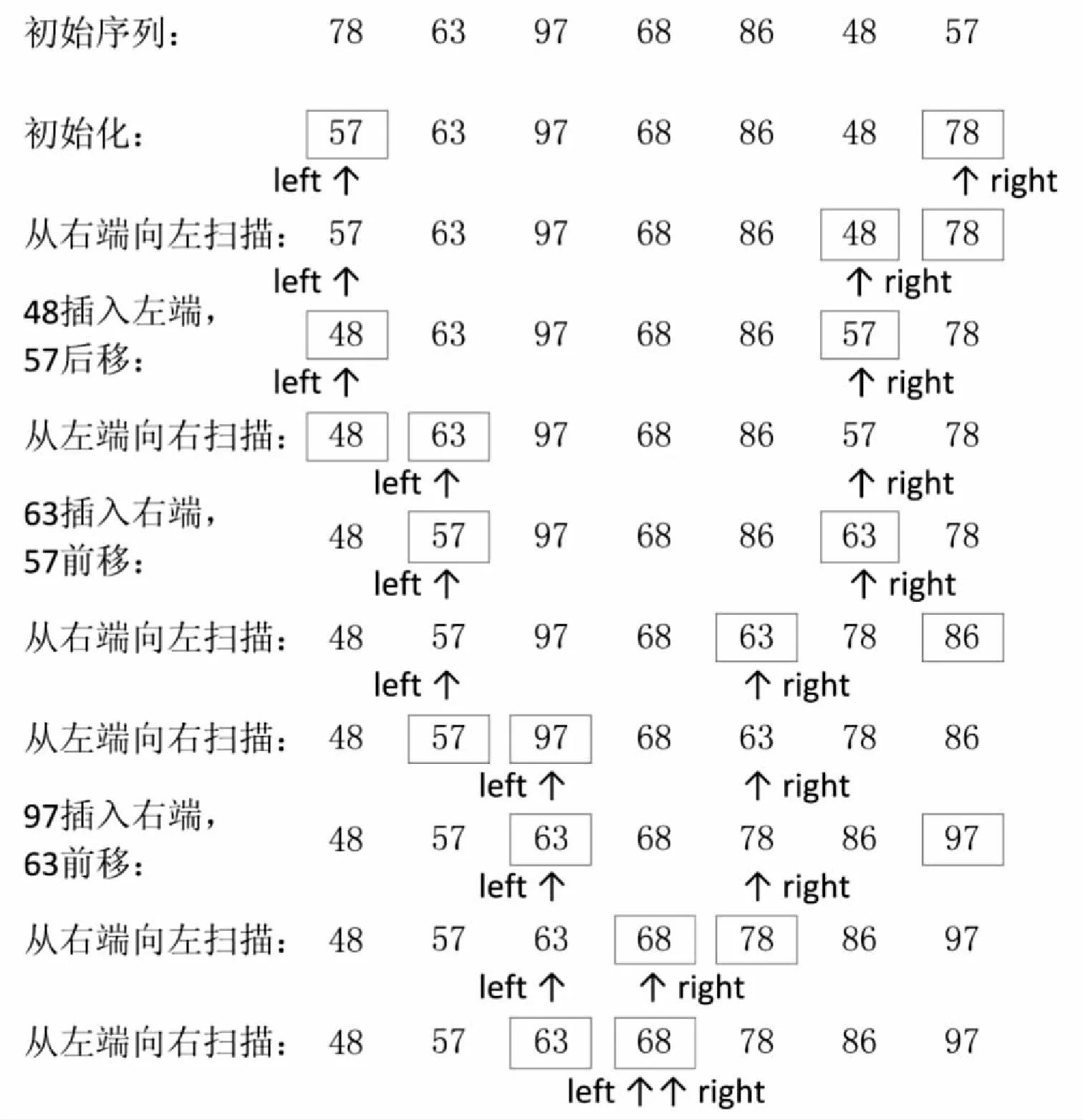
3.2 算法描述
3.3 算法分析
4 实验数据与结果
4.1 算法的数据比较和移动次数
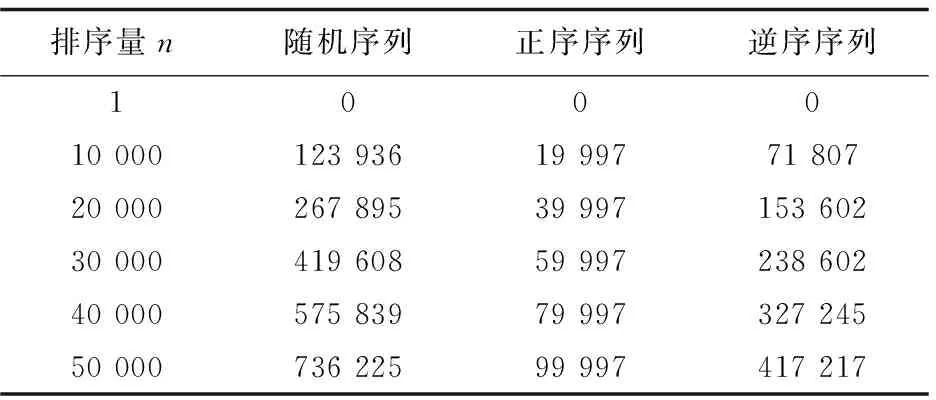
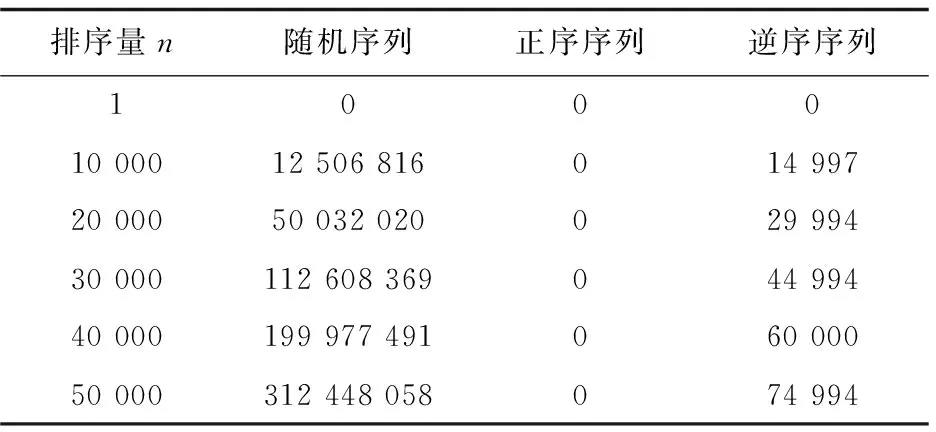
4.2 几种算法的比较





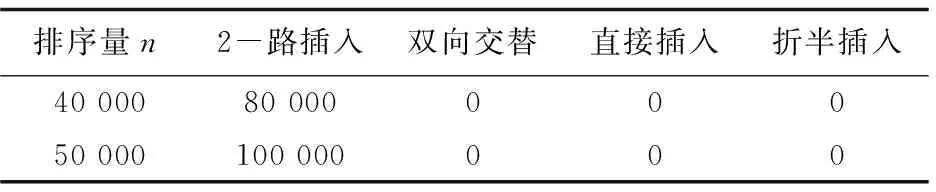


4.3 结 论
5 结束语

