大道至简,规避讨论
王晓


[摘 要] 分类讨论是解析数学问题十分常用的方法,但解析过程中对学生的分类能力、讨论思维有着较高的要求. 在实际解题时可以采用一定的策略方法来合理规避分类讨论,提高解题效率. 文章结合实例深入探讨数形结合、函数性质、分离参数、变换主元四种规避策略,提出相应建议.
[关键词] 规避;分类讨论;数形结合;函数;参数;主元
分类讨论是高中数学重要的解题思想和方法策略,可将复杂的问题拆分为若干个基本问题,解析时需分为“分类”和“讨论”两个过程,但对学生的解析思维有着较高的要求. 若分类的标准确定有误,很容易造成讨论的过程不完善,势必会造成解题错误. 从解法优化角度来看,在解题时若能转化思维角度或采用解题策略来简化甚至规避分类讨论,则可以提升解题效率,下面对规避策略加以探究.
渗透数形结合,规避分类讨论
数形结合在求解函数问题中有着广泛的应用,实际上该方法策略也可用于规避分类讨论,即求解某些代数类问题时,可以构造对应的函数,并绘制函数图像,利用函数图像的直观性来解题.该规避策略常用于涉及含参函数、方程、不等式等问题中.
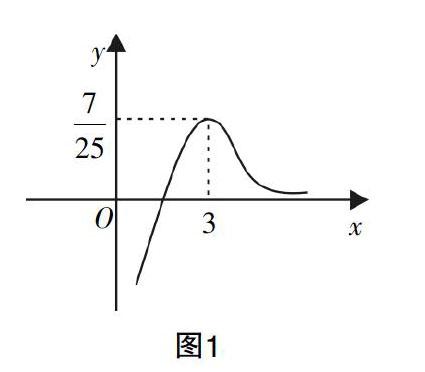
例1:ax3-x2+x+1=0是关于x的方程,已知该方程在(0,+∞)上的实数解有且仅有一个,试求实数a的取值范围.
分析:题干所给方程是一个含有参数a的关于x的一元三次方程,无法直接获得其解,常规解法是对a的取值范围加以讨论. 此时我们就可以采用数形结合的方法,基于方程构建相应的函数,通过研究函数的图像与x轴的交点个数来确定实数a的取值范围.
解:可将原方程变形为--=a,可设f(x)= --=(x>0),则f(x)的导函数为f′(x)=-. 分析可知在(0,3)上,函数f(x)单调递增,在(3,+∞)上单调递减,又可求得f(3)=>0,f(1)=-1,在(3,+∞)上f(x)>0. 从而可以绘制图1所示的图像,由图可知当a=或a≤0时函数与x轴有唯一的交点,即对应的方程在(0,+∞)上的实数解有且仅有一个,因此实数a的取值范围为aa=,a≤0 .
總结与指导:数形结合规避分类讨论的最大优势是图像直观,可以直接获得解题突破的关键信息. 但在学习时需要掌握解读函数图像的方法,能够从函数图像中提炼出曲线交点、变化趋势,值域、定义域,以及曲线之间的相对位置等内容,并能够用关系式来表示.
活用函数性质,规避分类讨论
函数性质在分析取值类问题中有着广泛的应用,对于一些涉及变量讨论的取值问题,则可以充分利用函数的性质来加以简化,规避讨论. 例如常用的函数对称性、单调性等. 一般利用函数性质来规避分类讨论时,需要根据题干性质提取原函数的关键性质,并用函数关系或不等式来具体化,逐步将问题转化为相应的方程组或不等式组.
例2:对于函数f(x),其在定义域[-1,1]上是偶函数,并且在区间[0,1]上单调递增,已知f(1+m) 分析:题干给出了函数f(x)的性质及单调区间,需要根据函数间的不等关系来求m的取值范围,常规的做法是讨论函数的定义域,确定每个区间上的情形,但该方法相对较为烦琐,此时就可以利用该函数的对称性来规避分类讨论. 函数f(x)是偶函数,则必然满足f(x)=f(-x)=f(x),后续只需要利用该对称性质来加以分析即可. 解:f(x)在定义域[-1,1]上是偶函数,则根据偶函数图像的对称性可知该函数满足f(x)=f(-x)=f(x),从而可将不等式转化为f(1+m) 总结与指导:函数性质是函数内容学习的重点,利用函数性质可以解决多类型问题,例如方程、不等式等问题. 而在学习时需要关注函数构建的方法,建立函数与方程、不等式之间的关系,掌握问题转化的技巧与思路. 合理分离参数,规避分类讨论 参数取值的不确定性是造成分类讨论的原因之一,因此在分析某些函数取值问题时,则可以考虑采用分离参数法,通过将参数与函数分离的方式来规避讨论. 在求解时首先对函数的参数进行分离,等价转化问题,一般将其转化为相应的不等式问题或函数取值问题,然后利用相关性质来对其取值加以分析. 例3:已知函数f(x)=-ax(x>0且x≠1),如果存在x∈[e,e2]使得f(x)≤成立,试求实数a的取值范围. 分析:函数f(x)内含有参数a,讨论特定条件下关于函数的不等式成立,而a的取值不确定,常规思路是设定分类标准,讨论对应条件下不等式成立的情形. 但该种思路相对较为烦琐,可以采用分离参数的方式,将参数a集中到不等式的一边,转化为函数的最值问题. 解:存在x∈[e,e2],使得f(x)≤成立,代入函数解析式,则有-ax≤,可将其变形为a≥-,则需要分析-的值域,可以构建函数g(x)=-,其中x∈[e,e2],则有a≥g(x)min. 通过分析g(x)的导函数可以确定函数g(x)在区间[e,e2]上单调递减,则g(x)min=g(e2)=-,即a≥-,所以实数a的取值范围为 总结与指导:分离参数是重要的数学方法,从表面上来看是将参数转移到符号的一侧,实际上是为了方便构建函数,利用函数的性质回避讨论. 需要注意的是在分离参数时要严格按照数学运算法变式,关注参数对应的取值. 灵活变换主元,规避分类讨论 对于某些含参不等式问题,如果从常规的角度来设定主元求解,有时需要对参数的取值加以讨论,其过程较为复杂,此时可以考虑采用变换主元的方法,即设定参数为不等式的主元,然后分析参数与未知数之间的变化,并借助相应的函数知识来对参数的取值加以讨论,从而获得最终答案. 例4:已知不等式mx2-2x-m+1<0,对于满足m≤2的一些m均成立,试求x的取值范围. 分析:上述为含参不等式,表面上是关于x的一元二次不等式,需要讨论满足成立条件下的m的取值. 为避免分类讨论则可以采用变换主元的策略,即将不等式视为是关于m的一元一次不等式,则对应的解集就为[-2,2],求x的取值范围,可以通过分析参数m与x的变化来完成. 解:根据不等式来设定函数,设f(m)=(x2-1)m+(1-2x),可将其设为是关于m的一次函数,对应的图像就为一条直线,根据题意可知当m∈[-2,2]时,直线位于y轴的下方,因此需要满足的条件为f(-2)<0,f(2)<0,可得不等式组-2x2-2x+3<0,2x2-2x-1<0,可解得 总结与指导:变换主元实际上是变换问题视角,在主元变换的过程中需要严格遵循函数、方程、不等式的设定要求. 在学习时需要引导学生关注知识本质,引导学生多角度看待问题,拓展解题视野. 解后深度反思,思考教学建议 分类讨论可以促进问题的条理性,但思维过程较为烦琐,需要确保讨论过程不“重”不“漏”,这也是在解析问题时要合理规避分类讨论的原因所在. 上述是对规避分类讨论四种策略的实例探究,下面基于突破过程提出两点建议. 建议1:关注问题转化的过程 从上述四种策略来看,规避分类讨论实际上就是转化问题视角,将对应问题转化为分析过程较为简洁的问题,例如转化为函数问题、不等式问题等. 因此在学习时需要关注问题转化的策略,学习知识之间的关联,如利用函数值域来分析不等式、方程取值. 一般问题转化时可以按照如下步骤进行:首先确定问题类型,思考对应的知识关联,结合知识联系点对问题等价转化,然后利用等价问题的性质定理来探究结论. 建议2:关注规避策略的思想 解題过程中所用的方法策略背后隐含的是数学思想,因此实际上就是在数学思想的指导下完成了思路构建,例如上述对问题转化就是化归转化思想的应用体现,而数形结合分析问题的过程中渗透着数形结合思想. 因此学习分类讨论的规避策略就需要立足对应数学思想,掌握数学思想的本质内涵,深刻理解思想方法解析问题的精髓所在. 数学思想与知识定理同等重要,在探究运用过程中可以提升自我的思维品质,因此在教学中需要教师重点引导,合理渗透. 总之,规避分类讨论的策略有很多,上述只是其中四种较为常用的,而规避过程实际上就是问题转化过程,该过程中需要学生深刻理解问题,破除思维定式,充分利用关联知识来合理转化. 而转化解题同样可以锻炼思维,因此对提升思维能力有着极大的帮助.

