落实三项举措 提高复习效率

李红梅

[摘  要] 应用题是高考必考题型，也是学生求解质量不高的题型，基于这个现状，文章提出了应用题复习的专题化设计的几个路径，复习中训练学生通过“圈读、解读、联读”等方法读全、读懂、读通题意，从而准确建模并强化运算求解的示范、训练，切实提升学生的应用题解题能力.

[关键词] 应用题;专题设计;阅读;运算

应用题教学是增强学生数学应用意识，提高数学建模和问题解决能力的重要途径. 应用题，贯穿整个基础教育学段，它不仅是实现数学育人、提升学生数学素养的重要内容，还是各类考试必选的题型. 应用题考查及题型创新，甚至成为高考命题设计的一大亮点. 然而调查发现，尽管应用题在高考配分上占有相当的权重（8.8%～10%），但在整个高三的复习安排中，应用题复习如何组织并未得到很好的落实，缺乏完整的专题设计;学生应用题求解的质量也普遍不高，2017年至2019年的三年之中，江苏省考生应用题平均得分率仅为0.40，还出现了得分率仅0.35的情况. 应用题，甚至成了一部分考生的“心理阴影”. 结合对应用题教与学的现状分析及本人的具体实践，要提高应用题复习的效果，必须精心落实好以下三项举措.

加强应用题复习的专题设计

专题复习是高三复习组织的基本形式. 专题通常以《课程标准》《考纲》为依据，从知识、方法、能力三个维度，立足于整个中学数学内容体系，进行整体设计. 通过系统的专题复习，使学生的认知结构更加清晰、完整，综合能力得到进一步提升. 在一定程度上，高三复习的专题设计及实施水平，直接影响学生的考场表现.

然而，纵观整个高三复习的现状，唯有应用题复习的专题化程度及实施质量是令人担忧的. 一是少见有应用题复习的专题设计，纵观现行的不知其数的高三复习资料，几乎没有哪本现成资料上有目标比较明确、专题比较突出、设计比较系统的应用题专题. 加之时间、精力、能力等诸多方面的原因，一线不少教师也无暇自主进行专题设计补充，往往只能停留于遇题讲题的离散状态. 二是应用题复习缺乏有力的“对症”性措施. 复习时，对学生在应用题方面究竟存在什么样的问题，查得不清、断得不准，对如何真正解决好学生存在的问题，办法不多、落实不力、训练不够.

应用题复习需要专题编设，需要有专题的复习安排. 应用题背景一般源自现实生产、生活，应用题大凡是出于考查数学知识、方法、能力的目的，通过逆向思维编制而成的. 应用题专题可以通过常见的模型为线索展开，如方程（组）型、不等式（组）型、函数型、统计（概率）型、线性规划型等;可以由背景属性为线索来组织，也可以由主要方法类型为线索展开，如平面几何图形性质分析、坐标解析法、数据分析法等;还可以从应用题求解的关键环节——阅读理解、模型建构、运算求解为线索组织. 应用题的专题编制可以在备课组内分工负责进行，在备课组集体对应用题复习的目标设定、内容组织、复习要点进行集体研究的基础上，按任务要求，进行合理分工、分头落实. 应用题专题复习，要在专门的集中的时间内进行，还可根据学生掌握的真实情况，采取集中专题训练与滚动式渗透性训练相结合.

突出应用题的阅读理解

阅读理解是应用题求解的基础. 数学应用题是所有数学问题中阅读难度最大的一类问题. 通常情况下，应用题语言是现实生产、生活中的语言，由于学生现实生活经历、经验的局限，需要学生对这种语言有较好的适应和准确的理解（生活语言数学化）. 应用题的文字阅读量较大，一般的应用题都在150字（符）以上，有的甚至超過200字. 而且应用题语句间，直接的逻辑联系不明显，学生要在3～5分钟内，读全——不遗漏任何一个信息点，读懂——理解每一句话的数学意义，读通——头脑中建立起每句话内在的关系和联系，不仅要注意力的高度集中，还需要有缜密的阅读思维，更需要较高的语言转化能力. 学生较多存在的应用题畏惧心理，首先就反映在难过应用题阅读关.

应用题阅读是有法可循的. 借助每一道具体问题，系统指导和培养学生“圈读”“解读”“联读”的习惯. “圈读”指的是指导学生在阅读过程中，及时进行标记（注），对题中重点、关键信息，尤其隐性、弱性信息进行标注;“解读”指的是在学生准确理解题中直接语言的基础上，对其语义的数学化理解及转化，它是阅读的关键;“联读”就是将题中各语句间的内在关系进行梳理，建立各信息点间的内在联系. 训练学生准确提取题中的“事件信息”“内容信息”和“问题信息”的能力，明确阅读的任务方向. 以下题为例：

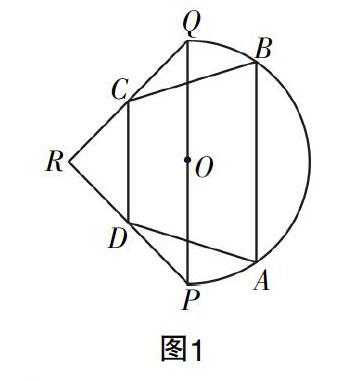
如图1，某市有一个健身公园，由一个直径PQ为2 km的半圆和一个以PQ为斜边的等腰直角三角形PRQ构成，其中O为PQ的中点.现准备在公园里建设一条四边形健康跑道ABCD，按实际需要，四边形ABCD的两个顶点C，D分别在线段QR，PR上，另外两个顶点A，B在半圆上，AB∥CD∥PQ，且AB，CD间的距离为1 km. 设四边形ABCD的周长为c km.

（2）求周长c的最大值.

该题中“事件信息”是要在一个由半圆及等腰直角三角形的组合图形内建一条四边形跑道. “内容信息”是半圆的直径是2 km，△PRQ是底边为2 km的等腰直角三角形，四边形ABCD是高为1 km的梯形. “问题信息”是求梯形周长的最大值. 本题的阅读难度在于读出四边形ABCD为等腰梯形和其中的一个主变量，从而建立起“周长”与该主变量之间的关系. 训练学生的“解读”能力，关键就是如何在不同的背景下，选择合适的主变量并找到相关量间的内在联系. 要准确“解读”题意，可从这几个方面进行分析：①对象的性状——是什么对象（图形结构、数量关系）;对象处于什么状态——确定的还是变化的. ②影响对象性状的关键因素——如本题中四边形ABCD的边还是角（大小、位置）. ③已知与所求间的内在联系——主变与因变的关系.

概言之，应用题阅读关键在于通过系统、持久的训练，使学生熟练掌握怎么读、读什么.

强化应用题运算实践

在不少时候，运算被误认为是一种“简单数学劳动”而被忽视. 尤其是在应用题训练中，无论是教还是学，往往习惯于以理解题意、建立关系为兴奋点，严谨合理的运算求解，通常被留着“课后”. 这种情形自初中“列方程（组）解应用题”开始，就被一直延续着，尤其到高中后，如果所列关系式的结构比较复杂，运算量较大时，为了所谓的节约课上的时间，都不愿在课堂上对具体的运算过程作充分的展开. 长此以往，造成了学生对应用题运算求解的重视不够、实践虚浮、能力不足，最终无论是学生平时的作业练习，还是考试的关键时刻，“列而不求”“求而多错”就成了一种常见现象. 连续几年的江苏高考分析报告指出，应用题运算求解失分所占比例一直很高. 分析中还发现，考生运算求解失分，主要由对“复杂”运算的畏惧心理、对运算路径缺乏合理的规划、对运算结果缺少严谨的“检验”（数据的背景意义关注不够）等原因造成的. 这些与学生平时缺乏扎实的运算实践都有内在的关系.

事实上，运算过程包含着多种数学素养成分——运算程序规划、最简路径设计、最优方法选择、换元转化思想等. 运算也是一种特定的数学思维，应受到高度重视. 面向高考的高三应用题复习，更要自觉强化运算求解环节的落实.

首先，要充分发挥好教对学的示范作用，课堂教学中要带着学生一起“算”. 要从运算程序的规划、法则的遵循、路径的选择、方法的优化、细节的推敲作全面展开. 要摒弃重结果轻过程的习惯，要在“算”的过程中挖掘和彰显数学运算所蕴含的智慧精彩. 要以“问题串”设计为抓手，使运算求解的过程成为“想着算”的过程. 如前所列题例中，若以CD长（设为2x）为主变量，则最终的关系式为c=2x+2+2（0

①根据运算式的结构特征及x的取值范围，通过什么途径，可使式子得到简化？（在嘗试比较后选择三角换元）所得简化式为c=2sinθ+2cosθ+2.

③你的下一步打算是什么？借助什么途径求得c的最大值？

其次，要严格对学生运算过程实践的要求，克服运算畏惧心理和惰性习惯. 平时的作业训练，要求学生提供具体的运算过程，并对“算法”选择作简要说明（因为习惯上的“化简、求解”的背后隐匿了太多虚空的东西）.

第三，要重视基于思维发散的路径优化训练. 应用题的解答是一项“大运动量”活动，运算求解只是其中最后一个环节，通常情况下，学生容易出现“体力不支”的现象而影响最后的运算投入. 路径探究，直接决定“模型”式的繁简及解题的运动总量. 还以前例为例，如果选择解析法：以O为原点，RO所在直线为x轴建立平面直角坐标系，设B（cosθ，sinθ），θ∈0

，，则比较容易地就能得出c=2sinθ+2cosθ+2. 同样，如果选择直线RO与OB构成的锐角θ为主变量建立模型，也能使求解的运算总量减轻.

最后，要强化运算细节的关注，应用题的运算求解，就运算对象而言，具有数据“大”及数据的实际意义规定的特点，如何通过“单位”转换将数据“化大为小”，如何始终关注数值的“取值范围”都是运算求解时特别重要的细节，细节往往决定成败.