带时间限制的托盘调配问题优化
陈 皓,程牟娟,李 平
(1.宜宾学院经济与管理学院,四川宜宾644000;2.西南交通大学交通运输与物流学院,四川成都611756)
在我国经济现代高速稳定的发展过程中,现代化物流的重要意义已经被大家所认知. 而物流标准化工具中,托盘作为物流产业基本搬运工具,在流通过程中被广泛的应用,与集装箱一起,被认为是世纪物流产业中两大关键性创新之一,被誉为“活动的地面”“移动的货台”.
但是,由于我国自然资源分布不均匀、地区经济发展不平衡、城市布局不尽如人意等因素,适合托盘运输的货源在地理位置布局及流量流向上存在明显的不平衡性,托盘物流在调运方向上存在明显的差异性. 因此,空托盘的空间调配问题,是我国现代托盘物流市场的一个重要理论研究方向,是现代物流托盘共用业务顺利开展的基础条件. 托盘调运一方面由于托盘供给量不足而产生物流等待时间较长;另一方面,一些托盘量富余的供给点由于富余的托盘存储,产生额外的仓储费用,更会影响托盘使用的效率. 于是就产生了空托盘在一段时间内,从托盘富足的供给地点运往稀缺地点的物流,随着这些空托盘的调用过程,产生一些无效的物流运输过程,造成物流生产的浪费. 但在托盘运输广泛发展的现代物流中,空托盘的调配问题也日益突显出来.
在共用托盘调配和空托盘回收方面的研究,国外起步相对较早,有大量的成果已经运用到了实践之中,也积累了相对成熟的理论研究. Jouglard 等人对英国托盘物流的实际流通情况进行研究,提出建设共用托盘系统的必要性,共用系统可以减少不必要的装卸环节,降低物流成本,提高物流效率[1]. Ray等人采集13 家美国大型零售公司的托盘使用情况后,开展了共用托盘租赁服务,并计算租赁托盘的费用收取情况,通过仿真计算出使用共用托盘系统的企业,比自主准备托盘运输的企业的低5美元[2].
相对来说,我国对托盘调运模型和托盘共用模式的研究起步较晚,但发展速度很快,也取得了一定成果. 李晓等人指出共用托盘的使用以及托盘租赁体系的建立,能进一步加速我国物流行业现阶段联合作业的运营组织,能有效地提高托盘的利用效率,降低物流成本,简化运营组织;并在理论基础上进一步对托盘租赁企业在进行物流利益分配时的分配策略进行了理论研究[3]. 章雪岩对托盘共用系统的概念模型进行了分析研究,就概念模型在物流市场的应用进行了理论分析,为深入研究共用托盘系统奠定了理论基础[4]. 游玲君在研究铁路空托盘调运过程中,针对铁路运输的特点,以供给、需求、能力、库存、租赁等多因素影响条件为约束条件,建立多目标规划模型,借助lingo 枚举性求解共用托盘调度优化问题[5]. 周康等人在对空托盘调度过程的研究中,将运输网络按节点进行拆分细化,考虑租赁成本、运输成本、库存成本、调运时间及总调运费用之间的关系,针对实际情况构建最优模型,同时考虑客户对托盘需求量和需求时效的约束,利用ILOG Cplex 优化软件对模型求解[6-7].
尽管国内外专家学者对托盘共用系统的运营模式、平台建立等进行了初步研究,奠定了理论研究的坚实基础,但仅有少许文献对托盘共用系统的调度模型进行分析;且由于租赁因素的存在,对托盘供给时间没有硬性要求,这与现代物流追求安全高效的理念不符. 本文针对托盘调运前提下,一定范围区域内存在托盘供需点失衡的情况,进行空托盘的统一调配方案进行定量化研究. 理论上来说,空托盘的调配不仅与集装箱的空箱调运有相似之处[8-9],但也具有制造成本相对低廉储备量较大,制造工艺简单易于生产商复制生产,自身体积较小调运较方便的特性. 因此,当空托盘的调运距离或费用较高或需求托盘的时间较为急切时,可以考虑在需求点附近直接租赁、购买甚者制造托盘来满足需求. 因此,本文充分考虑空托盘调运的费用、时间等影响因素,引入较大的惩罚系数和阶跃函数以空托盘调配费用最小和调用时间最短为目标,建立优化模型,以供给、需求、装卸、运输车等为约束,应用改进的遗传退火算法,对多目标优化进行满意解的计算.
1 模型构建
1.1 网络描述及符号说明
(1)有铁路运输网G=(V,E),表示铁路网中的车站节点和连接线路.
(2)V={vk|v1,v2,…,vn} 表示车站节点集,n表示车站节点数量;在节点中,VI={vi} ={v1,v2,…,vp} ,VI为托盘供应点的集合,VJ={vj} ={vp+1,vp+2,…,vn} ,VJ为托盘需求点的集合,p≤n.
(3)在托盘供应点vi(i∈I)的托盘供应量为Si;tiz表示单位托盘在节点i的装载时间;CLi表示单位托盘在节点i的装载成本;hoi表示节点vi托盘的库存成本;Miz表示节点vi处运输车量的最大储备数.
(4)在托盘需求点vj(j∈J),有属性vj=(xij,Cij);xij表示i→j的托盘运送量;Cij表示i→j的运输车;包含Cij={Kij,Qij,uij} 分别表示运输车单车容量、i→j间单车每公里平均运输成本、i→j间车辆运输速度.tjx表示单位托盘在节点j的卸车时间;CUj表示单位托盘卸载成本为.
(5)Dj表示需求点vj的需求量;ETj表示需求点vj期望最早到达时间,LTj表示需求点vj期望最晚到达时间;需求点vj可选择租赁托盘,Rj表示需租赁托盘数,rdj表示单位托盘租赁时的租金和运输成本,租赁时装卸时间和费用与2、3点中取值相同;ηj表示需求点vj缺少托盘时,单位托盘惩罚成本ηj(ηj≫rdj).
(6)在连接线路集合E中,E={emn|m,n=1,2,…,nm≠n} 表示连接车站节点间的线路集;emn表示连接线路的距离表示某流向托盘的运输路径与区间m→n的关联系数,取1 表示区间m→n在其运输径路上,取0为否.
1.2 目标函数
(1)总成本最少
托盘运输总成本决定了托盘配送的最优组织方案,构成托盘运输总成本包括托盘运输成本、剩余托盘的库存成本、托盘调运的装卸成本、托盘不足时租赁托盘的租金、托盘不足时的惩罚成本.
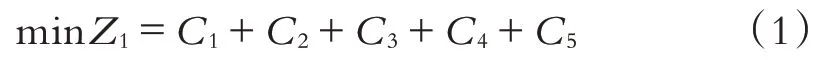
式中:C1是托盘运输过程中的运输成本(元);C2为剩余托盘的库存成本(元);C3为托盘调运过程中产生的装卸成本(元);C4为托盘供应不足时,需要另行租赁托盘产生的成本(元);C5是缺少托盘进行运输所产生的惩罚成本(元).
其计算方法如下:
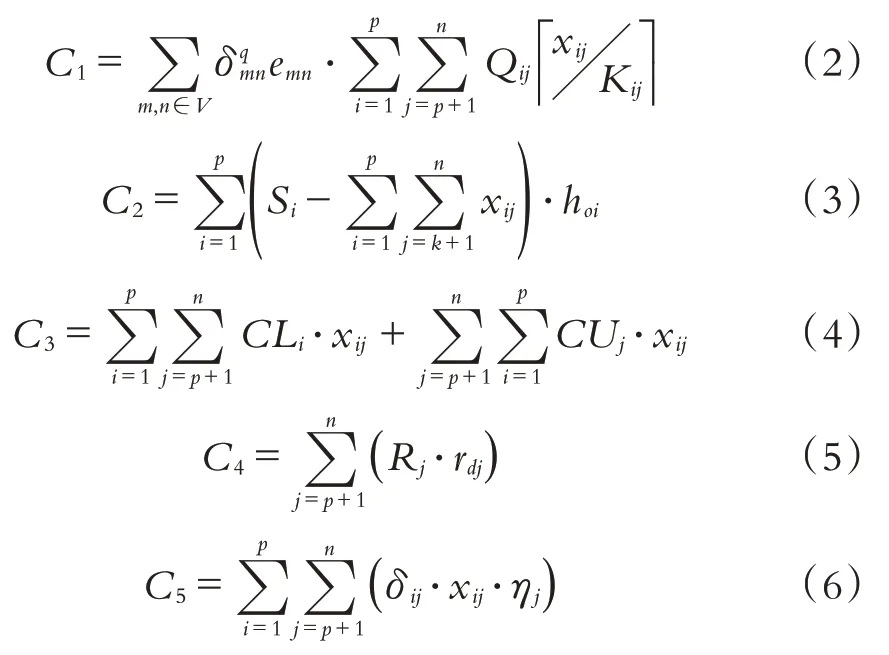
式中:表示向上取整.
(2)运到时限
这是托盘调配的一个重要影响因素,尤其是托盘运到时间晚于需求点的最迟需求时限时,会极大延误物流的正常组织.其计算公式为:

式中:Tj为托盘运到j站的实际时间(小时).
1.3 约束条件
(1)托盘供给约束,即需求点的总供给量xij之和小于供给点供应量Si之和:

(2)托盘需求约束,即托盘需求点vj的需求总量数不大于供给量xij与租赁量Rj之和:

(3)托盘供需点的装卸能力约束,即车站的装卸能力满足托盘送达时间应在最早期望送达时间和最晚允许送达时间之间:

由于租赁托盘可提前运输,缺少托盘的惩罚成本ηtj≫rdj,故租赁和缺少托盘不考虑装卸时效约束.
(4)供应节点发车能力约束,即节点vi使用的运输车辆数不大于该节点运输车量的最大储备数:

式中:K为单车车辆最大装载托盘数量,nmn为线路emn流向上现有的通行能力.
1.4 模型构建
综合以上内容,以产生的调配费用少和托盘需求点的时间延误小为双重目标,以供给、需求、装卸、运送能力为约束条件,建立多目标的托盘调配模型:

2 多目标模型算法设计
在解决一定规模的托盘运输优化问题中,由于既要考虑运输的时效问题,又要考虑运输费用,是多个子目标共同优化的NP 问题,且这些子目标之间并非正相关,很难找到一组解使得多目标优化模型的各个子目标同时达到最优,通常只能求得模型的Pareto最优解.
2.1 多目标优化的概念
对于具有多个目标的优化问题,min{Z1(x),…,Zn(x)},如果{x} ,{y} 分别为该问题的两组可解集,其对应的各子目标函数值记为{Z1(x),Z2(x),…,Zn(x)}和{Z1(y),Z2(y),…,Zn(y)}.
定义1当且仅当∀i=1,2,…n,Zi(x)≤Zi(y),且∀j=1,2,…n,Zj(x)≤Zj(y)时,可行解x对可行解y占优.
定义2在Pareto最优解中,如果有x★满足目标函数组{Z1(x★),…,Zn(x★)},对 于所有 的x,不存 在Zi(x)<Zi(x★),则称可行解为x★Pareto最优解.
2.2 算法设计
考虑到文本模型和求解的复杂性,拟采取遗传退火算法进行求解,其基本思路是,首先随机产生初始种群,执行基本遗传算子后,按照某种策略生成邻域种群,然后针对两种群个体分别执行Metropolics选择,并下降温度. 本文借鉴SA-GA 算法机理,对算子进行适当修改,应用于有时间限制的托盘运输调度问题[10].
(1)初始编码形成:为了解决该组合优化问题,选择数组P=(P1,P2,…,Pm)作为一个染色体,表示从1→m流向上的托盘运输路径,其中染色体的基因片段Pi为托盘运输所经过的路径,即Pi=(vi,…,vm).
(2)适应度函数:令最终目标函数都有两个适应度值,对于不联通路径或不满足时间约束,引入惩罚系数M(M为一个大数)和阶跃函数J( )
x.
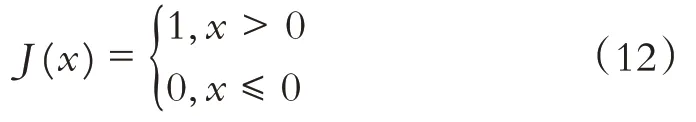
可将目标函数改进为:

(3)算子选择:本文采取按适应度值的大小来计算选择比例,适应度值越大的个体,被选中成为父代的概率就越大,每次按适应度比例随机挑选两个父体,进行下一步的操作.
(4)交叉方式:在数组P=( )P1,P2,…,Pm中,按照步骤(3)中方式,选择两个不同流向的托盘运输车,其走行径路代表的基因片段记为( )v1,v2,…,vm和随机选择两段基因中的某个公共节点此时交换两个基因片段在vi节点后的染色体,得到两组不同的子代染色体,分别记为交叉算法的进行如图1所示.

图1 交叉方式Fig.1 Cross mode
(5)变异算子:对于变异方式,采用随机选择部分路径节点,重新排列的方式. 即在径路的基因组上随机选择两个节点,保持节点外侧的基因序列不变,节点间的序列进行重新翻转排列、合并,新的基因就作为变异算子序列.
(6)模拟退火策略:在遗传退火算法中,采用遗传算法能较快的找到最优解的搜索方向,迭代得出最优解或满意解,而模拟退火在对局部最优解的邻域搜索功能,能提升算法跳出局部解获取全局最优的能力. 因此,结合遗传算法和模拟退火算法,可以进一步提高组合优化算法对最优解的求解能力. 在进行迭代的过程中,对完成遗传策略的子代种群,进一步选择当前个体chrom(i),按照(5)中的变异方式,产生一个邻域个体chrom(j),然后使用Metropolics 策略对当前个体进行替换:

式中:p(i→j)为当前个体chrom(i)被领域个体chrom(j)替换的概率,f(i)、f(j)为当前个体chrom(i)和变异个体chrom(j)的适应度,T为当前温度.
2.3 算法流程
利用组合遗传算法求解托盘调配优化选择问题的实施流程步骤如下:
步骤1:初始参数设计,包括初始种群数popsize,交叉概率和变异概率分别调整为Pjc、Pby,终止的子代代数Maxend.
步骤2:按照式1 中的方案生成初始种群pop,设置当前代数n←1.
步骤3:计算初始种群中个体的染色体适应度值,按照式3中“轮盘赌”规则,生成父代个体的种群.
步骤4:按式4、式5 中的规则,进行交叉算子和变异算子操作,获取新的子代种群.
步骤5:根据式11 中的计算,在子代种群中选择一个chrom(i),生成其领域的chrom(j),并更新当前的迭代代数为n←n+1.
步骤6:当迭代代数n满足n≥Maxend时,算法终止,否则转步骤3进行循环计算.
步骤7:对算法终止时,输出的种群最优的染色体进行解码,解码后的方案即为托盘调配的最优方案.
3 案例分析
设计有铁路网G=(V,E),其中V=(v1,v2,v3,v4,v5,v6),E={Emn}. 有六个托盘节点,其中两处为托盘供应点,记为v1、v2;四处为托盘需求点记为v3、v4、v5、v6. 节点之间均为双向连接,路网拓扑图及路段属性如图2、表1所示.
供 应 点v1、v2的供应量为S1= 5000 片,S2=5500片,存储成本CL1=CL2= 0.15元,托盘装车时间为t1z=t2z= 0.0006 h,车站运输车量空闲数M1z=M2z= 4 辆,所有运输线路的运输速度uij=60 km/h. 供应点v1、v2车辆发车、路线、容量、运输成本等属性如表2 所示. 需求点运到时限、租赁成本、卸载时间等属性如表3所示.

图2 路网拓扑图Fig.2 Road network topology

表1 路段属性表Table 1 Road section properties
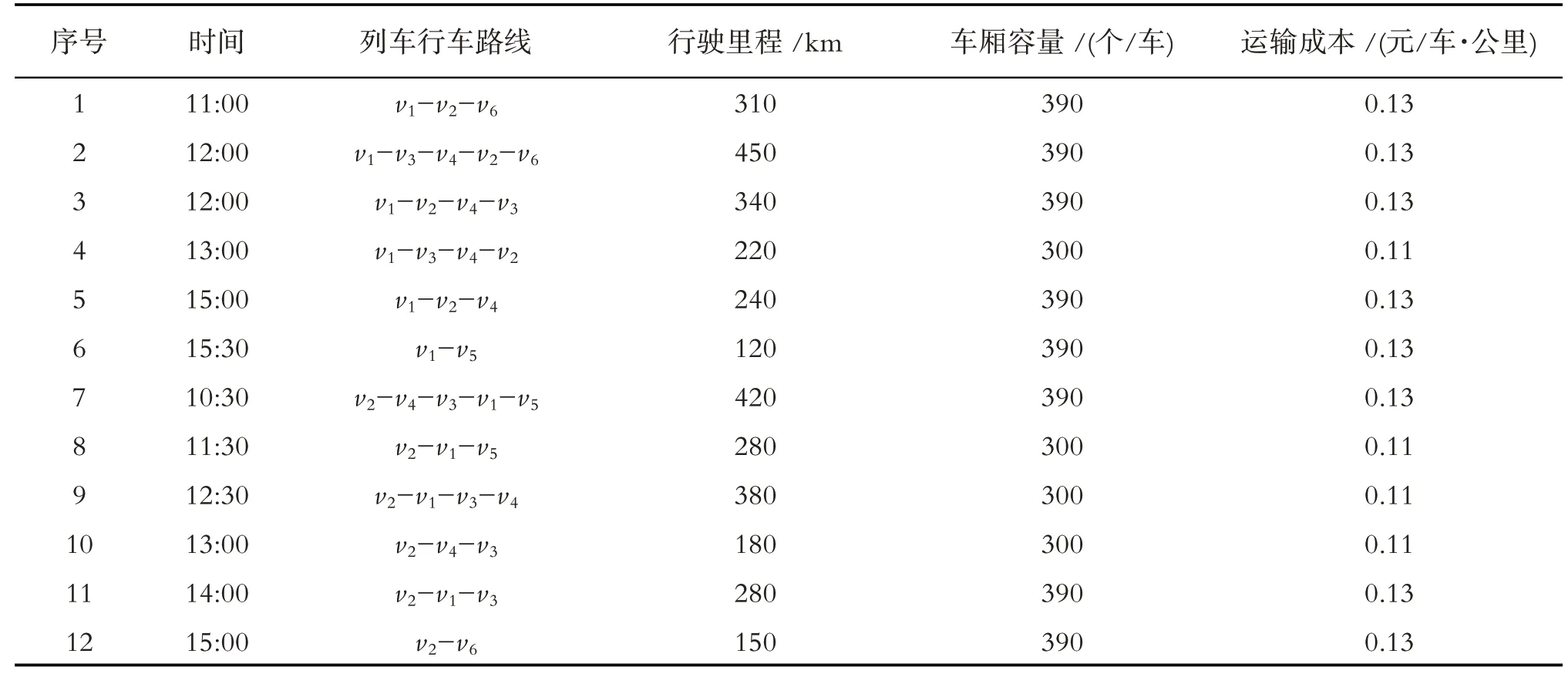
表2 各供应点运输情况Table 2 Transportation of each supply point

表3 各需求点需求情况表(成本单位:元/片)Table 3 Demand of each demand point(yuan/piece)
3.1 算法求解
将前文所述的模型,按以往经验进行调整,确定组合优化算法的参数值设计为:种群popsize=60,交叉概率Pjc=0.75,变异概率Pby=0.05,初始温度T0=999,结束温度Tend=0.01,温度衰减参数α=0.87,终止迭代代数Maxend=100,每次对物流最优径路求解并对出发-到达时间进行调整. 当对任意一个父代执行完选择、交叉、变异方式后,遗传部分停止,转入模拟退火Metropolics 选择. 整个计算过程基于MATLAB 7.0 软件求解,最终得到目标函数最优的染色体为:

其中,每组基因表示[供给点,运输序号,需求点,托盘调配个数].
解码后满意解如表4所示.
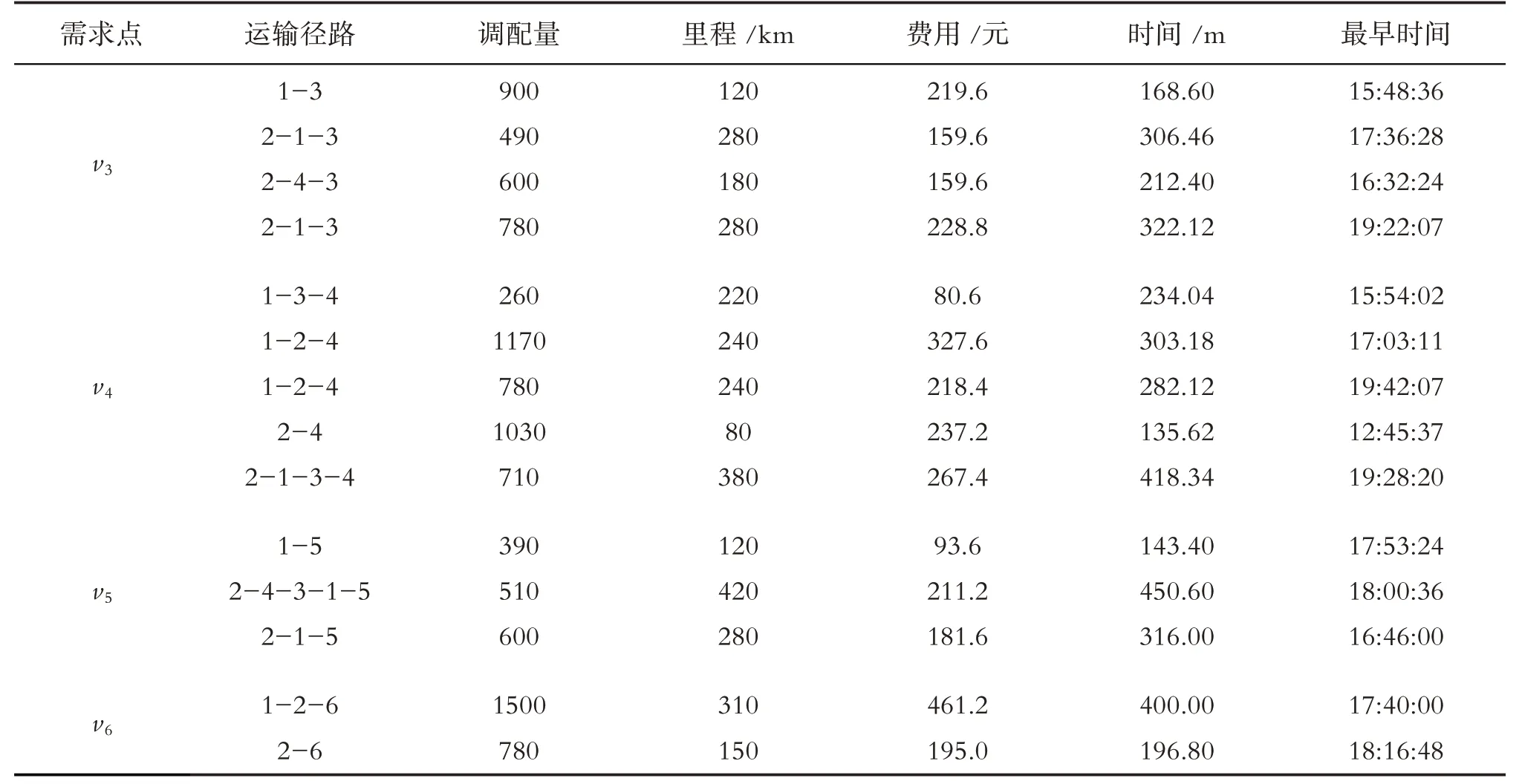
表4 托盘调配方案选择结果Table 4 Selection results of pallet deployment scheme
此外,在v3还需租赁托盘430个,租赁费用6 837元,此时目标函数适应度值为:Z1=9878.4 元,Z2=88.72分钟.
3.2 算法对比
将本文方法与基本遗传算法在求解有时间限制的托盘调配问题进行对比. 在不改变遗传算法种群popsize、交叉概率Pjc、变异概率Pby、迭代代数Maxend的基础上,遗传算法获得的最优的染色体为:

此时,在v3节点上仍需租赁托盘430 个,目标函数适应度值为:Z1=9981.2 元,Z2=88.72 分钟. 可以看出,利用本文的改进遗传模拟退火算法,比基本遗传算法在解决托盘调配问题上,更易获得最优解或近似最优解.
4 结论
本文改进型遗传脱货算法适合于小规模托盘调配的物流组织优化,如果供给和需求节点较多时,可先将大规模地区划分为若干小区域后再进行调配优化. 同时,本文算法中还可以根据实际情况,补充其他约束条件,如来往返线路距离不等、不同车辆和不同经路上运输速度不等、需求点的托盘需求权重不同等. 一般情况下约束越多,问题就越复杂,求解起来就越困难,但往往也越符合实际情况.

