极限平衡和数值方法在边坡工程中的应用

秦鹏飞

（郑州铁路职业技术学院铁道工程学院，河南郑州 451000）

边坡及边坡稳定是土木、水利、矿山、交通等工程建设中需要研究和解决的难点问题，由于人为因素的干扰和自然因素的侵袭，近年来我国多个省份和地区发生了严重的滑坡事故。边坡的稳定性分析和治理研究具有重大的学术意义和工程价值，一直受到岩土工程工作者的广泛关注和重视［1-5］。作为边坡稳定分析主流和发展较快的分析方法，刚体极限平衡法和计算机数值分析方法目前已取得了许多重要的研究成果［6-7］。本文旨在对边坡稳定性分析方法最新进展及工程应用进行分析述评，希望能为推动边坡工程治理的精细化管理和精细化水平作出贡献。

1 刚体极限平衡法

刚体极限平衡法是以刚体极限平衡理论为基础，假定滑动面发生刚性滑动破坏而进行边坡失稳分析的物理方法。其求解思路是以摩尔—库仑的抗剪强度理论为基础，将潜在滑动面范围内的坡体按一定比例剖分为若干条块，然后根据条块间的极限平衡条件建立静力平衡方程，进而根据方程计算坡体的安全系数并评价坡体的稳定性［8-9］。滑动面可以假定为折线形或圆弧形，根据所假定滑动面形状的不同而采用不同的计算方法。

1.1 简化Bishop法

简化Bishop法较Fellenius平面应变问题分析方法的优势在于考虑了条块间的水平作用力，因而计算结果具有更高的准确度。简化Bishop法假定滑面为圆弧形（见图1），它在计算中忽略了条间的竖向剪力作用，是非严格条分法，但在均质土坡稳定性的分析中，简化Bishop法的计算精度与考虑竖向剪力的严格法基本一致，因而在工程分析中具有广泛的适用性。简化Bishop法是目前《建筑边坡工程技术规范》推荐采用的计算方法，计算公式：

式中，Mr和Ms分别为抗滑力矩和滑动力矩；Ni为土条i底部的法向力；Wi为土条i重力；ci、φi为土条i抗剪强度参数；αi为土条i底部的倾角；li为土条i长度。

苏振宁等［10］采用积分中值定理推导了任意滑面简化Bishop法的安全系数计算式（式（2）），使简化Bishop法适宜于非圆弧滑面的计算，拓展了它的工程应用范围。

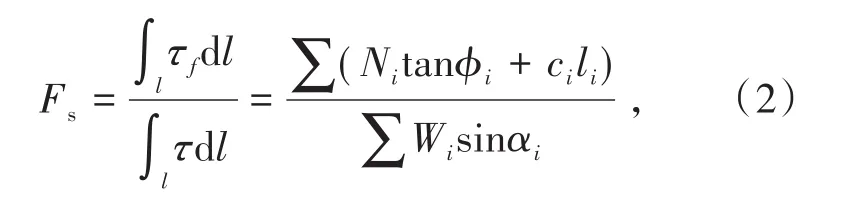
卢玉林等［11］假定浸润线为抛物线形式，推导了渗流作用下粘土边坡安全系数的简化Bishop法计算式（式（3）），并通过计算机程序实现了数值解。算例表明该方法具有较高的可靠性，可为渗流作用下边坡的稳定分析提供参考。

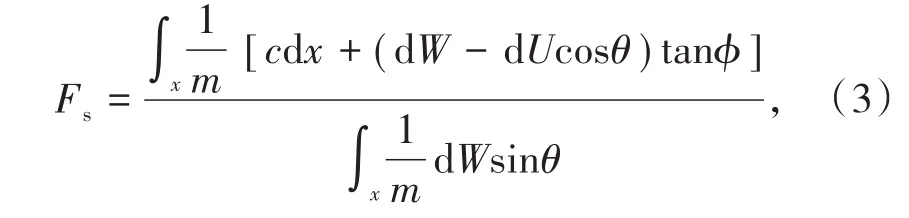
式中，m为隐式系数；m=cosθ(1+tanφtanθ/F)；W为土条自重；U为水土压力。

1.2 Morgenstern-Prince法

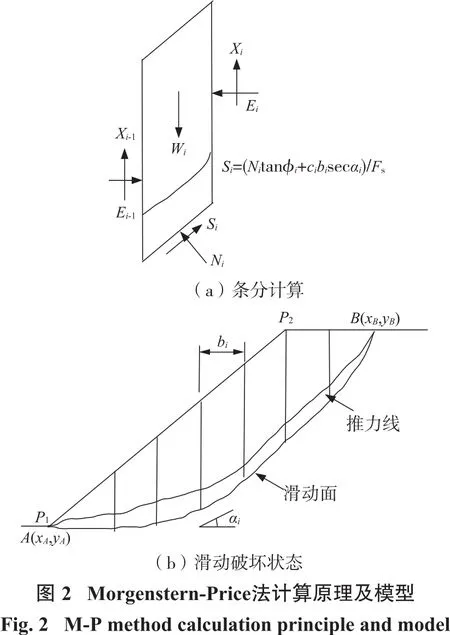
Morgenstern-Price法是严格条分法，其每一条块均能严格满足力和力矩的平衡条件，且M-P法不要求滑面是圆弧形的，适宜于更一般情形下边坡的稳定分析计算（见图2）。M-P法建立的平衡方程数目较多，为便于计算在平衡分析中引入了条间力函数f（x），并假定条块剪切力X与法向力E满足关系式X=λf（x）E，λ为比例常数。当f（x）取常数1时，Morgenstern-Price法与严格分析法Spencer法等价。

朱大勇等［12］对传统M-P法安全系数Fs的计算方法进行了改进，建立了易于编程的安全系数Fs和比例常数λ的迭代计算公式（见式（4）、式（5）），只需经过简单迭代便可得到快速稳定的收敛解。

式中，R为抗滑力；T为下滑力；ψ为传递系数；Kc为地震影响系数；Q为坡面上外荷载；ω为其与竖线夹角。

邓东平等［13］通过改变条分数、边坡高度和边坡角度等参数，采用M-P法对圆弧和任意滑面形状边坡的稳定性进行了计算，结果发现条间力函数f（x）取0.1、0.5、1.0或半正弦函数对计算结果影响不大；梁冠亭等［14］采用改进的M-P法对抗滑桩支护边坡的稳定性进行了计算，通过引入自适应遗传算法准确地搜寻到了坡体最危险滑动面的位置，并分析得到了支护结构的受力规律及其与边坡稳定性的关系。

1.3 通用条分法

通用条分法（General Limit Equilibrium method）是基于静力平衡方程的一般形式及其边界条件，严格考虑所有力和力矩的平衡所建立的条分方法。通用条分法所得结果是理论意义上的最严格解，能广泛应用于任意形状滑面的边坡稳定分析和安全系数的计算。通用条分法力和力矩的平衡方程计算见式（6）、式（7）所示。

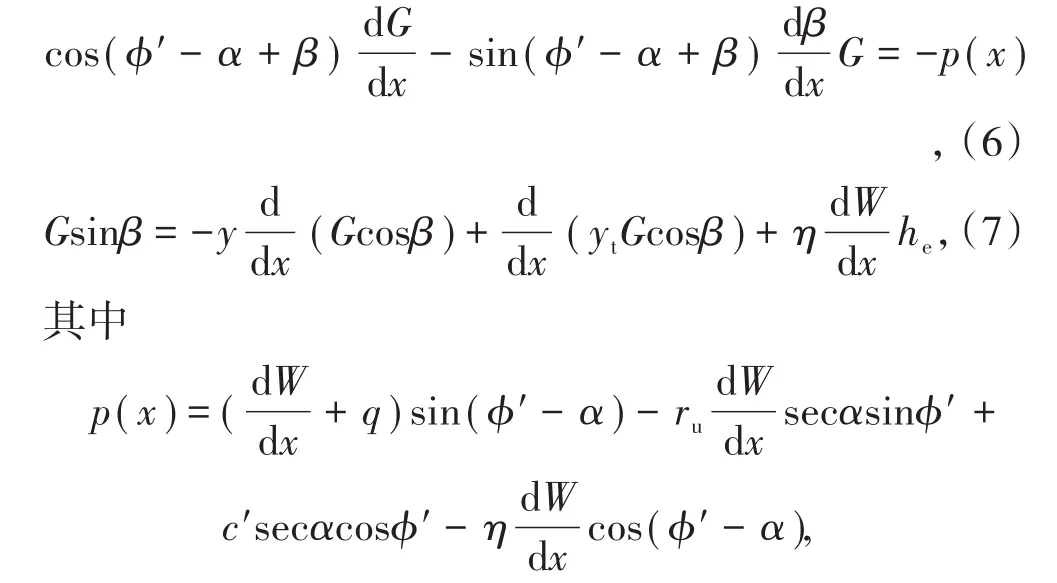
式中，G为土条垂直侧边上的总作用力；W为土条自重；α为坡面倾角；β为作用力G与水平线的夹角。

陈祖煜等［15-18］在分析Fredlund普遍极限平衡法的基础上推导出边坡稳定静力微分方程的闭合解，并编制了相应的求解计算程序STAB，为通用条分法的工程应用作出了重要贡献。各种极限平衡分析方法基本原理见表1所示。

2 强度折减数值计算法

强度折减数值计算方法（Strength Reduction Numerical Calculation Method）可以考虑边坡失稳破坏过程中土的应力—应变关系，随着高性能计算机技术的发展和岩土强度理论的进步，数值计算方法如有限 元 法（Plaxis、ABAQUS）［19-22］、离散元法（PFC、3DEC）［23-25］、边界元法（BEM）［26］和拉格朗日元法（FLAC）［27］等已取得了许多积极的研究成果，并在工程分析中发挥着举足轻重的作用。

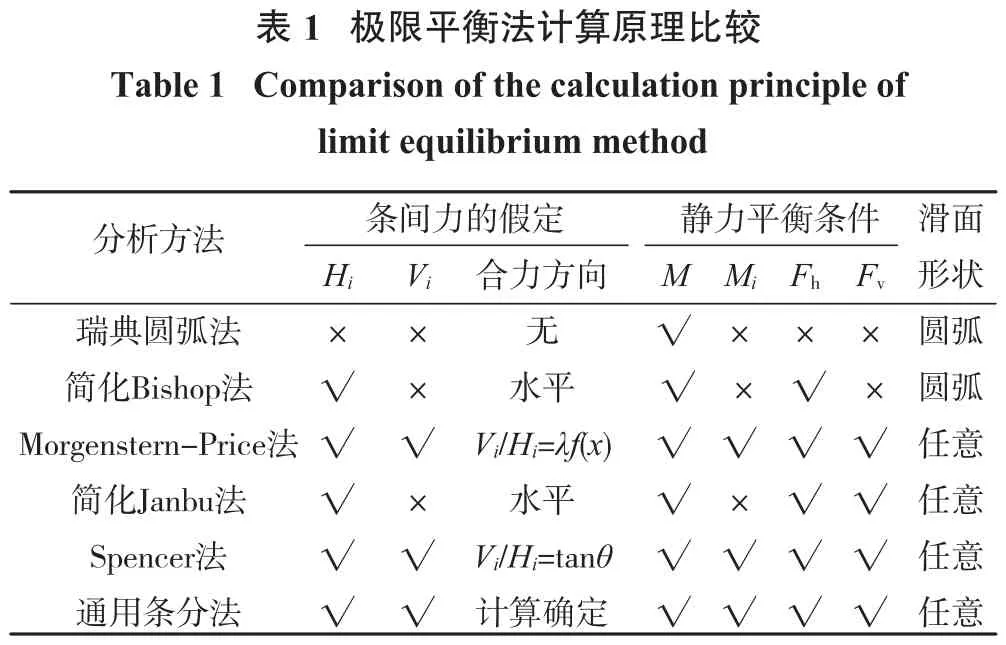
注：M为整体力矩平衡，Mi为条块i力矩平衡，Fh为条块水平方向力的平衡，Fv为条块垂直方向力的平衡，θ为滑动面平均坡度。

2.1 计算原理

强度折减数值计算方法的基本原理是，将岩土材料的黏聚力和内摩擦角等抗剪强度参数进行折减（式（8）），用折减后的参数进行边坡的稳定性分析计算。不断降低强度参数直至边坡失稳破坏为止，破坏时的折减数值即为坡体的安全系数。

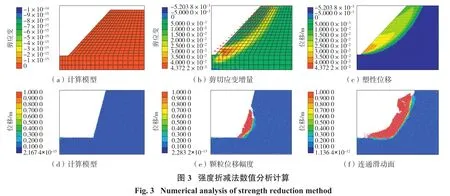
式中，c和cF分别为折减前后土体的黏聚力；φ和φF则为折减前后的内摩擦角；F为强度折减系数。强度折减法不需要作繁琐的条分计算，也不需要假定潜在滑动面的位置和形状，程序可严格依照实际地质条件分析坡体滑动破坏的自然过程［28-29］。图3分别为采用FLAC3D和PFC2D计算得到的某黏质土坡安全系数、剪切应变增量云图及速度矢量图等，计算结果可以为相关工程的设计和安全评判提供可靠的参考和依据。

2.2 失稳判据

强度折减法通常以位移突变、塑性区贯通和数值计算不收敛作为边坡失稳的判据。具体来说：①坡顶的竖直位移或坡脚的水平位移突然大幅度增加，则认为边坡失稳；②坡脚至坡顶的塑性区范围不断扩大直至贯通，则认为边坡失稳；③程序计算无限制运行，无收敛迹象则认为边坡失稳［30-32］。

对于严格遵从弹塑性本构关系的理想岩土体边坡，上述3种失稳判据具有较好的一致性，而对于成分复杂的高陡边坡这3种判据则存在较大偏差。为解决失稳判据选取上的争议，陈力华等［33］提出考虑“张拉—剪切破坏的强度折减法”，主张将坡体渐进破坏过程中的抗拉强度同幅度折减（见式（9）），结果表明考虑张拉强度折减的计算方法在失稳判据上具有较高的一致性和准确性；

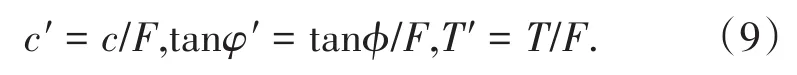
周正军等［34］指出边坡的失稳破坏模式与所采用的岩土屈服强度准则密切相关，目前广泛应用于边坡稳定分析中的Drucker-Prager准则和Mohr-Coulomb准则不能准确反映土体的抗拉强度，应予以适当折减和修正；李永亮等［35］指出岩土本构模型和计算参数、迭代计算算法及收敛容差等均会影响边坡的稳定性，为准确衡量边坡的失稳破坏状况应联合多种判据进行综合分析，对于均质、非均质、土—岩组合边坡和岩质边坡，建议分别采取①（主）+②（辅）、②（主）+①（辅）、②（主）+①（辅）和③（主）+①（辅）相结合的边坡失稳分析方法；等。

2.3 折减方法改进

边坡失稳破坏过程具有渐进性和局部化特征，物理机制表现为坡体局部强度降低，岩土材料出现应变软化，应力转移进而引起塑性区贯通。赵炼恒等［36］指出强度参数c和φ在边坡失稳过程中不是同时折损的，采用单一折减系数F进行等比例折减存在较大的不合理性，为此他基于双强度（c、φ）折减的方法提出边坡安全系数的隐式函数表达式（见式（10）），并编制非线性规划程序迭代求解，对准确求解安全系数具有参考价值。

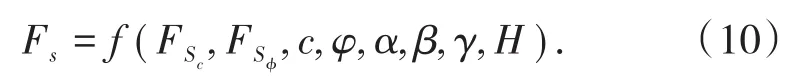
陈国庆等［37-38］指出坡体真实失稳破坏过程中只有滑动带的强度参数受损减小，而强度折减法忽略了滑动区和未滑动区土体强度的差异性致使计算获得的塑性区偏大，为此提出动态、整体相结合的强度折减法，即由动态强度折减法搜寻确定滑动面，由整体强度折减法计算安全系数，为强度折减法作出了重要改进。李世贵等［39］以岩土材料的极限剪应变作为坡体失稳破坏的判据，建立了模拟边坡破坏的极限应变—动态局部强度折减法，并采用离散元程序UDEC进行模拟和验证，结果表明该方法在坡体稳定性评价和渐进性破坏分析方面具有较高的可靠性。

3 结语

本文阐释了以简化Bishop法、Morgenstern-Price法和通用条分法为代表的刚体极限平衡法的基本原理、主要特点和功能优势，并从计算方法、失稳判据和折减改进等方面对强度折减数值方法进行了分析，阐述了2种方法在工程应用中的研究进展。边坡工程分析方法的进步，必将推动边坡工程治理向着精细化水平迈进。