基于自适应鲁棒的电液伺服转台双马达同步控制

郑 宇，张志龙，施卫科，张 健，安 东，孙京阳

(中国运载火箭技术研究院 空间物理重点实验室，北京 100076)

引言

转台是航空航天半实物仿真系统的重要装备[1]，主要用来惯导系统在空中的位姿，以对其追踪性能进行测试。转台一般有三个自由度，分别模拟惯导系统的俯仰、偏航和滚转。对于大型转台，外部还扩展了两个自由度，作为红外目标模拟器，即大型五轴转台。这种大扭矩转台一般采用卧式布局，外框由2个液压马达同时驱动，其扭矩大，可以实现很高的加速度和很快的响应速度。然而由于存在外框的机械耦合和中框偏心旋转带来的惯量扰动，对外框2个马达的同步控制带来很大挑战。国内外学者对此进行了大量研究[2-8]。其中自适应鲁棒控制器[9-10]结合了自适应控制器和滑模控制器的优点，即能够应对系统的不确定参数，同时对非结构不确定性有很强的鲁棒性[11-12],是提高转台双马跟踪和同步性能的有效手段。

然而，自适应鲁棒的控制效果很大程度上依赖于建模精度。目前针对转台的同步控制方法均是将由中框偏心旋转带来的惯量扰动作为干扰来进行处理，不能有效的改善2个马达的跟踪和同步性能。为此，本研究推导了转台的详细动力学模型，该模型考虑了外框机械耦合和中框惯量扰动对2个马达的影响。基于该模型，提出了变惯量自适应鲁棒同步控制算法。通过Lyapunov方法证明，选择合适的控制器增益，该算法可以保证系统的跟踪误差和同步误差同时收敛到一定邻域。最后基于Simulink仿真，通过与传统的PID控制器对比，验证了该算法的有效性。

1 转台建模

1.1 建模假设

图1为所研究双马达驱动电液伺服转台的结构简图，是典型的三自由度卧式转台。转台采用O形外框，由2个液压马达同时驱动绕俯仰轴运动；中框为U形，由1个液压伺服马达单端驱动绕偏航轴运动；内框由力矩电机驱动绕滚转轴运动。零位时，O形外框位于垂直平面内。

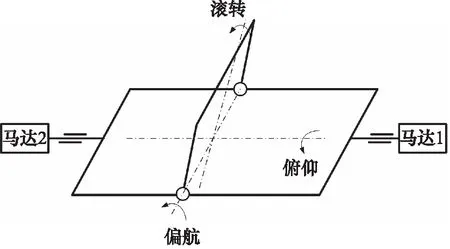
图1 卧式转台结构简图

由于本研究主要考虑外框2个马达的同步控制，为简化建模流程，给出如下假设：

假设1：忽略内框沿滚转轴旋转的偏心影响；

假设2：将中框运动等效为质点绕偏航轴的旋转运动；

假设3：认为马达1与外框刚性固连，马达2与外框的连接刚度为K；

假设4：由于马达的频宽远高于转台的机械频宽，因此忽略马达的动态特性。

对于假设3，由于外框的刚度很大，可以用马达1的转角来近似外框的转角。实际使用中，为马达1安装旋转编码器测量外框角度和角速度；马达2与外框的连接轴上安装力矩传感器，测量其与外框的角度差。

1.2 转台动力学模型

简化后的系统模型如图2所示，其中J1，J2，Jo分别为马达1、马达2、外框的等效旋转惯量；m为中框与内框的等效质点；d为中框等效质点的偏心距；α1，α2分别为马达1、马达2绕俯仰轴的旋转角度；β为中框绕偏航轴的旋转角度；T1，T2分别为马达1、马达2处的合力矩。

图2 坐标系

建立如图坐标系，其中原点O位于外框中心；Y轴平行于俯仰轴并指向马达1；Z轴通过圆心并垂直向上。

建立沿Y轴旋转方向的力矩平衡方程：

(1)

(2)

其中J′=J1+Jo+m(sinβd)2为转台与马达1的等效总惯量；g为重力加速度。式(1)为转台与马达1的力矩平衡方程；式(2)为马达2的力矩平衡方程。

1.3 摩擦力模型

仅考虑2个马达的黏性摩擦力矩和库伦摩擦力矩：

(3)

其中,τfi为马达i的摩擦力矩；cfi为黏性摩擦系数；bfi为库伦摩擦系数；Sgn(·)为符号函数。因此合力矩可以表达为：

Ti=ui-τfi

(4)

其中，ui为马达i的力矩输入。将式(3)、式(4)带入式(1)、式(2)，并将结果写成矩阵形式，得到系统动力学模型：

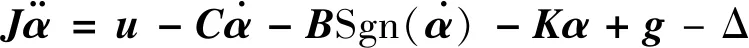
(5)

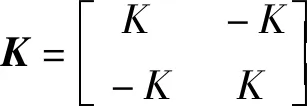
从系统模型(5)可以看出，其惯量矩阵是时变非线性的，等效总惯量J′体现了中框旋转造成的惯量扰动对系统的影响。

重新定义如下状态变量：

(6)

由此可得系统状态方程如下：

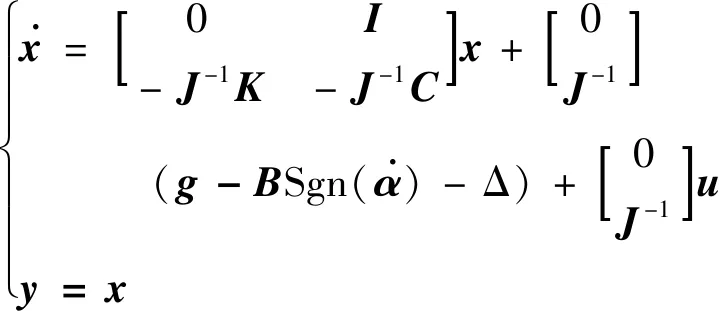
其中,x=[x1,x2]T，y为系统输出。定义系统误差变量：

(7)

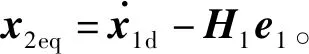
(8)

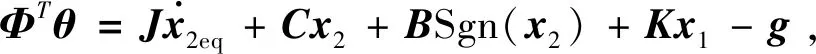
假设5：系统所有的不确定性参数和集中不确定性都是有界的，即满足：

(9)

其中,θmin=[θ1min,θ2min,…,θ8min]为不确定性参数的下界常数向量；θmax=[θ1max,θ2max,…,θ8max]为不确定性参数的上界常数向量；δ为已知正向量，始终为2个向量各元素的比较。

2 变惯量自适应鲁棒同步控制(ARSCI)

针对转台实际工作中，外框两侧马达由于机械耦合、变惯量干扰等原因造成的不同步问题，本研究所设计控制器旨在保证转台外框跟踪性能的基础上，进一步减小两侧马达的同步误差，从而提高转台的运动性能。

2.1 不连续映射与参数自适应律

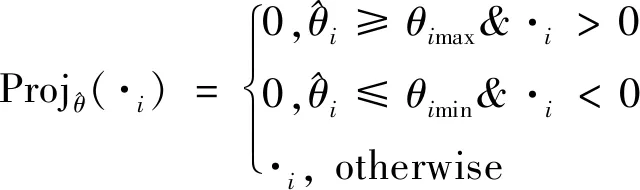
(10)

其中，i=1,…,8。采用如下自适应律：

(11)

其中，Γ为正定的自适应律参数矩阵，τ为需要后续章节设计的自适应函数向量。对于任意自适应函数τ，不连续映射式(10)均具备以下性质：

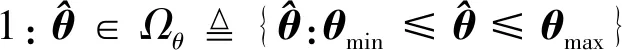
2.2 自适应鲁棒同步控制器设计

给定如下控制率：

u=ua+us,us=us1+us2

(12)

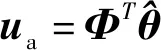
(13)

其中,ε为任意小正数，代表了对集中不确定性的抑制水平。由文献[13]可以给出非线性鲁棒补偿项的一种表达形式：

其中,ξ为正向量，其每个元素满足：

ξi≥||Φi||||θM||+δi

其中,Φi为Φ的第i列；θM=θmax-θmin；δi为δ的第i个元素。

系统控制框图如图3所示。

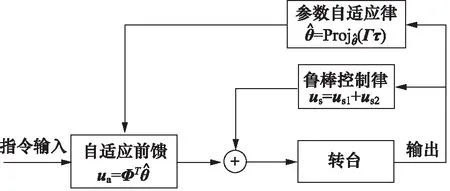
图3 控制框图

2.2 控制器性能分析

设计如下Lyapunov函数：

V(t)=eTΛ1e

(14)

其中

显然,Λ1和J均为正定矩阵，因此V(t)也是正定的。

对控制律(12)给出如下定理：

给定如下自适应函数：

τ=ΦTe2

(15)

且设定合适的参数矩阵H1，H2使得如下矩阵Λ2正定：

则控制律(12)保证：

(1) 系统所有状态变量有界，且李雅普诺夫函数满足如下约束：

(2) 如果不存在集中不确性参数，即Δ=0，则系统所有状态变量渐进收敛，即当t→∞时，e→0。

证明：对Lyapunov函数(14)两边求导，并带入式(8)和控制律(12)可得：

利用不等式(13)可得：

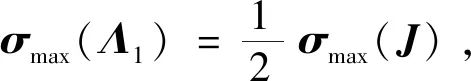
为证定理(2)，重新定义以下Lyapunov函数：

对上式两边同时求导，假设Δ=0，并带入自适应律(11)和自适应函数(15)可得：

由不连续映射的性质2和不等式(13)可得：

由此定理(2)得证。

值得注意的是，定理(1)表明，无论自适应函数如何选取，只要选择合适的增益，所设计控制器都能保证所有系统状态收敛到一定领域内。自适应参数的收敛方向是确保所有系统状态收敛到此领域，而不是朝向其真实值。

3 仿真研究

3.1 仿真对比

设置以下两组仿真，以验证所提算法的有效性：

(1) PID：2个马达均采用PID控制器。控制器参数为：KP=15000，KI=1000,KD=30000；

(2) ARSCI：采用变惯量自适应鲁棒同步控制。控制器参数H1=diag(5000, 5000)，H2=diag(2000, 2000)；自适应参数矩阵Γ=diag(0.01,0.01,0.001,1e6,0.1,0.1,1,1)；不确定性参数初始值θ0=[40.6，0.6，0.6，8000，5，5，40，40]；不确定性参数上界θmax=[46，16.25，1，15000，10，10，100，100]；不确定性参数下界θmin=[35.5，0，0.5，5000，2，2，20，20]。

输入曲线分别采用0.5 Hz低频和2 Hz高频正弦曲线：

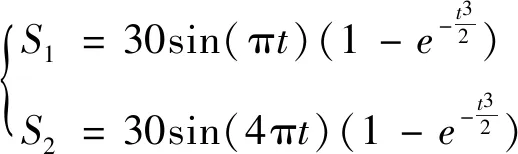
运动过程中，中框做转角为30°的1 Hz正弦运动。仿真参数见表1。

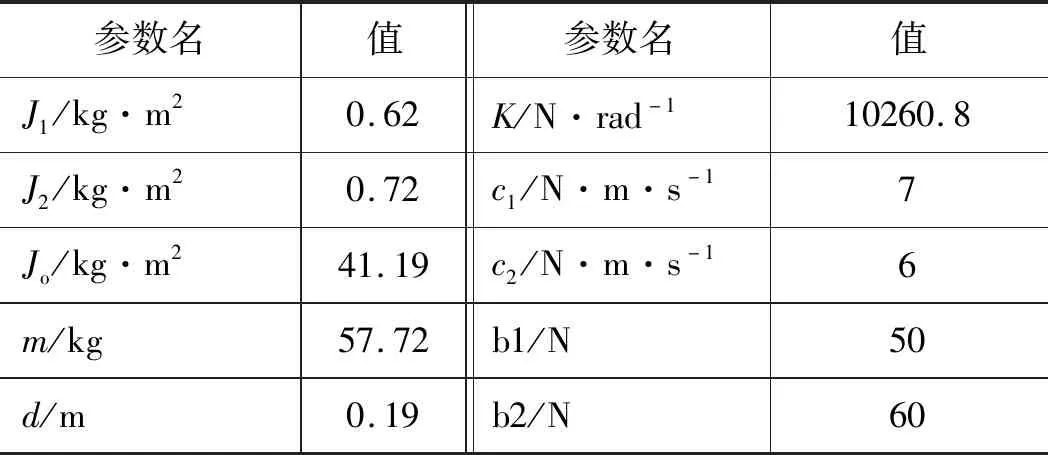
表1 仿真参数

3.2 仿真结果

图4和图5分别给出了低频输入指令下，PID控制器和ARSCI控制器的外框跟踪误差曲线，即αd-α1。PID控制器下，最大跟踪误差0.2°，且呈周期性变化；虽然ARSCV控制器的初始跟踪误差为0.2°，但15 s 后迅速收敛至0附近，这是因为在仿真模型中，集中不确性为0，符合定理(2)的结论。

图6和图7为低频输入指令下，PID控制器和ARSCV控制器的同步误差曲线，即α1-α2。PID控制器，最大同步误差为0.2°；ARSCI控制器最大同步误差0.1°，且迅速收敛到0。由此可见低频输入下，ARSCI的跟踪和同步性能均显著优于传统的PID控制器。

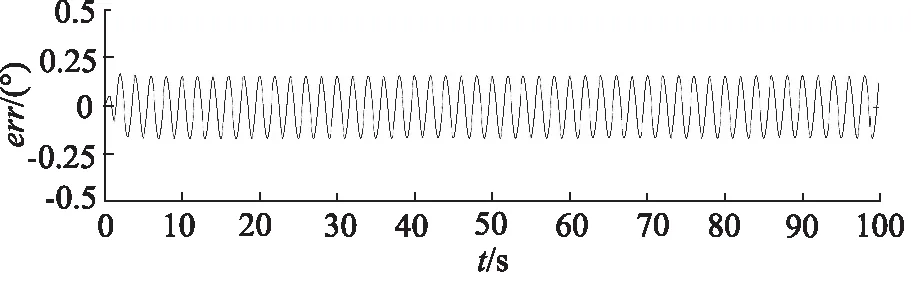
图4 低频与PID控制器下的跟踪误差

图5 低频与ARSCI控制器下的跟踪误差

图6 低频与PID控制器下的同步误差

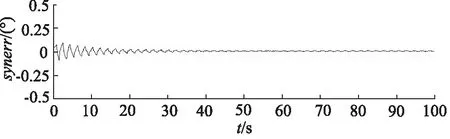
图7 低频与ARSCI控制器下的同步误差

图8和图9为高频输入指令下，PID控制器和ARSCI控制器的外框跟踪误差曲线。与图4相比，高频下PID控制器的跟踪误差显著增大，而ARSCI控制的跟踪性能没有显著变化。

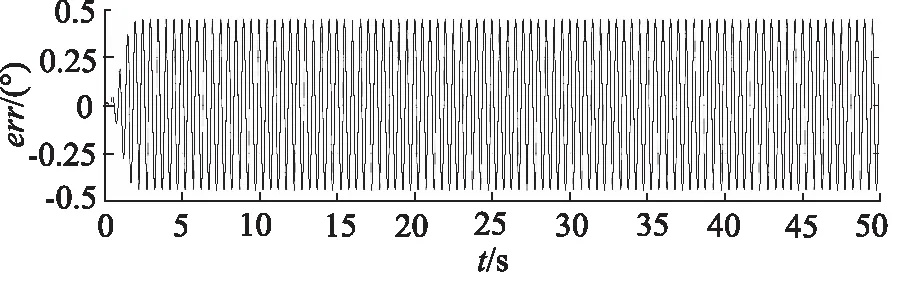
图8 高频与PID控制器下的跟踪误差

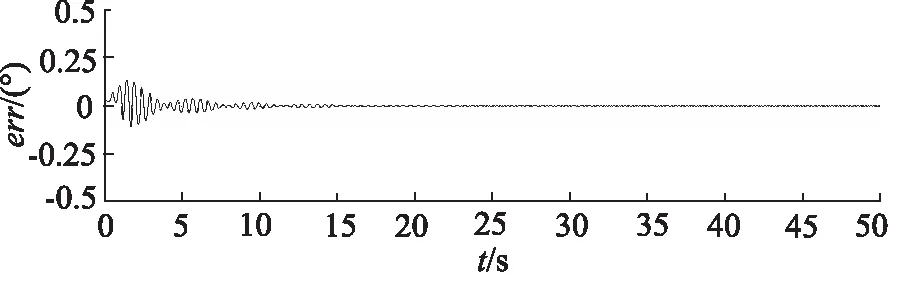
图9 高频与ARSCI控制器下的跟踪误差

图10和图11分别为高频输入指令下，PID控制器和ARSCI控制器的同步误差输入。可见传统PID控制器在不改变控制器参数的情况下，高频性能迅速衰减。而ARSCI的跟踪和同步性能在低频和高频输入下均能保证优异的性能。

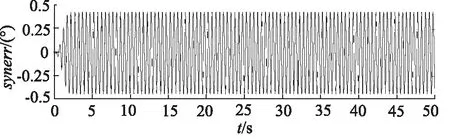
图10 高频与PID控制器下的同步误差

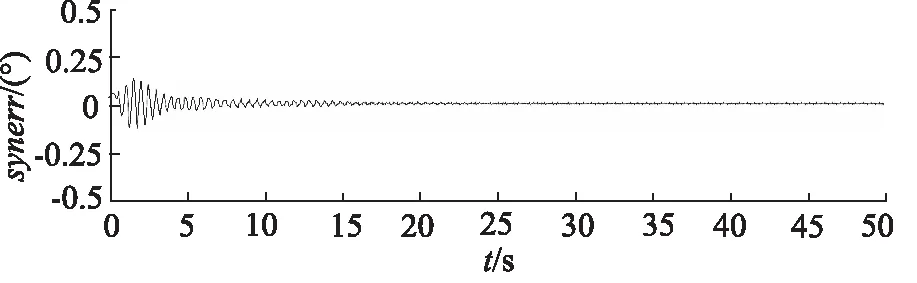
图11 高频与ARSCI控制器下的同步误差

图12和图13分别给出了低频和高频输入指令下，ARSCI控制器不确定性参数在自适应控制率下的收敛情况。可见，随着时间的推移，所有不确定性参数均收敛到特定值。但是收敛值并不是参数的真实值。根据所给出的定理，参数的收敛方向是确保系统状态变量收敛。

图12 低频下ARSCI不确定性参数变化

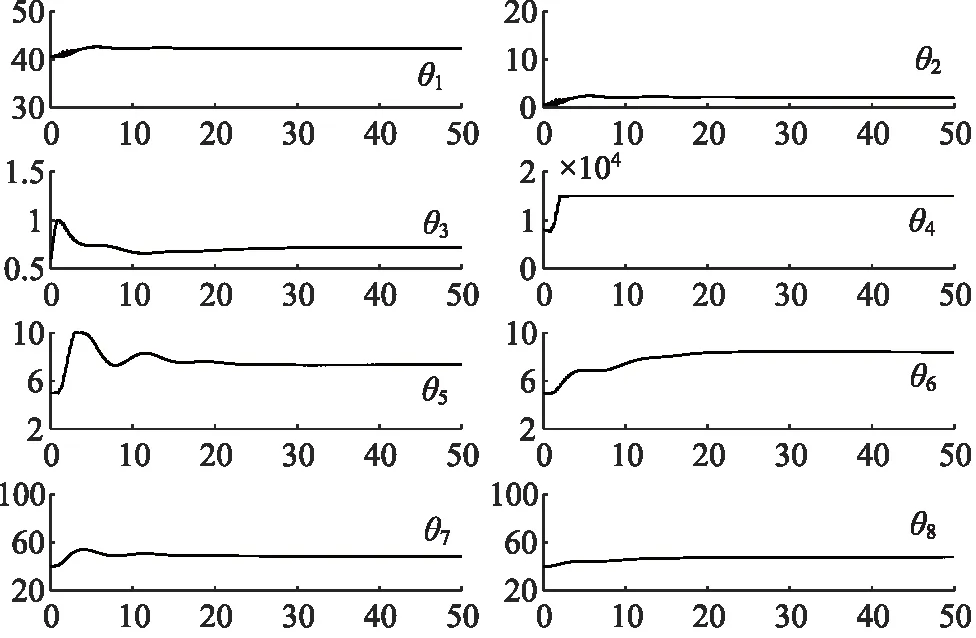
图13 高频下ARSCI不确定性参数变化

4 结论

本研究针对卧式电液伺服转台外框马达的同步问题，推导了转台的详细动力学模型。该模型考虑由中框旋转造成的惯量扰动对外框驱动马达的影响。根据所推导的模型，提出了变惯量自适应鲁棒同步控制算法，通过Lyapunov方法，证明所提控制算法的稳定性。仿真研究表明，所提算法在低频和高频下，均能保证系统的跟踪和同步性能，且随着时间的推移，跟踪误差和同步误差均收敛到一定领域。

同时，从仿真结果也可以看出，所给出的自适应控制率保证不确定性参数向系统误差减小的方向收敛，显然该方向不一定是不确定性参数的真实值。如何能够在确保系统误差减小的同时，保证不确定性参数收敛到真实值，是本研究未来的主要工作。