基于扩展干扰观测器的主动升沉补偿系统自适应鲁棒控制

范 珂，李世振，刘延俊，

(1.山东大学 机械工程学院，山东 济南 250100； 2.山东大学 海洋研究院，山东 青岛 266237)

引言

近年来，海上施工作业的需求不断增加，例如海上风机吊装、油气开采、救援等。在海上作业时，由于条件严苛，相关起重系统必须满足精度、安全、效率等作业要求。船体升沉运动导致的动态负载会严重影响起重机的使用寿命和操作精度[1-2]。

为了补偿升沉运动，减小动态负载，国内外学者进行了一些相关研究。DRISCOLL等[3]设计了基于蓄能器被动补偿装置来补偿线缆的动态张力和负载的垂直运动。被动补偿装置能耗小，但控制精度低，难以达到现代海上作业的精度要求，主动升沉补偿系统可以极大地提高补偿精度，因此被广泛用于海工装备中。主动升沉补偿系统，主体由电液伺服系统和运动测量单元(MRU)组成。电液伺服系统自身具有强非线性和建模不确定性，例如输入饱和、摩擦、液压油弹性模量随温度变化等[4]。不确定性的存在会使基于标称系统设计的控制器失稳或性能降阶[5-6]。此外，严苛多变的海上环境带来的外部干扰因此传统线性控制策略难以满足系统高性能要求，需要设计能有效抑制不确定性的先进非线性控制器。KUACHLER S等[2]设计了基于输出反馈线性化的非线性控制器并应用于海上吊机中，但是该控制器并没有考虑建模不确定性及外部干扰，极大影响了控制精度。DO K D等[7]设计了基于李雅普诺夫直接法的非线性控制器，用于双作用液压缸的电液系统中。NEUPERT等[8]设计了基于干扰解耦控制器的绞车式升沉补偿系统。ZHAO B等[9]提出一种应用于直流电机的积分鲁棒控制器，可处理任意连续可微且有界的建模不确定性。文献[10]采用滑模控制处理电液系统的不确定性。上述控制器为抑制外部干扰不可避免地要增大反馈增益，导致抖振甚至失稳，并且滑模控制器和李雅普诺夫再设计法只能处理匹配的不确定性[11]。采用干扰观测器对外部干扰进行估计，进而作为前馈项在非线性控制器中进行实时补偿，可以有效地抑制外部干扰。文献[12]中提出了一种非线性干扰观测器用于机械臂的运动控制中。这种非线性干扰观测器需要建立外部干扰的精确模型，然而海上环境多变，海浪为不规则波，电液系统参数变化等使得外部干扰无法建模。

针对以上问题，本研究提出一种基于反步设计的自适应鲁棒控制器，并应用于主动升沉补偿系统中如图1所示。电液系统摩擦、时变的内泄漏系数等因素使得系统方程存在不匹配的不确定性，反步法则可以放宽匹配条件[13-14]。将外部干扰及建模不确定性视为总扰动，利用扩展状态观测器估计其作用并实时补偿。扩展状态观测器不需扰动的精确数学模型，不需传感器直接测量扰动的作用。基于不连续投影设计自适应律以保证参数估计有界性。设计非线性鲁棒反馈项提高系统的鲁棒性，并减少与自适应控制律之间的耦合。最后，仿真结果验证了所设计控制器的有效性。

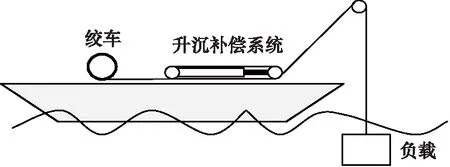
图1 主动升沉补偿系统

1 系统建模

采用MRU测量负载升沉运动，以生成控制器的期望轨迹。如图2所示，主动升沉补偿系统(AHC)的电液系统由阀控液压缸组成。AHC以MRU信号作为期望轨迹主动补偿有效负载的垂直运动，并克服系统摩擦力。目标是使活塞杆精确跟踪期望轨迹。下面建立AHC系统的非线性动态模型。

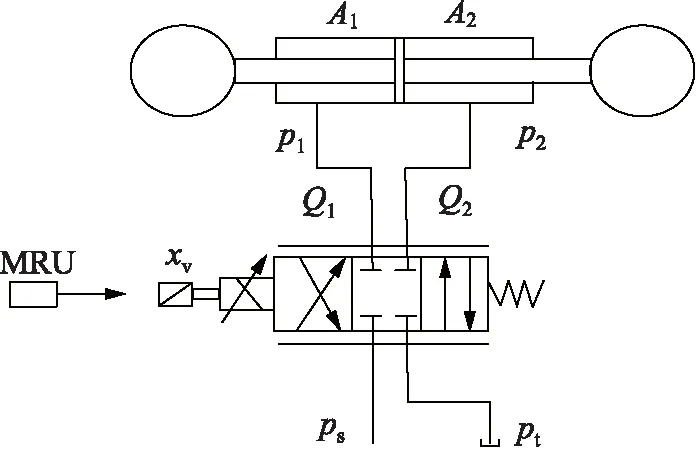
图2 AHC液压原理图

系统动态方程为

(1)

式中，m—— 等效质量

xp—— 液压缸位移

p1,p2—— 液压缸两腔压力

A1,A2—— 液压缸两腔有效作用面积

bH—— 系统等效阻尼系数

Fd—— 负载所受由水动力产生的拖曳力

负载所受拖曳力为[14]:

(2)

式中，ρw—— 水密度

Aload—— 入水区负载的等效截面积

Cw—— 入水区阻力系数

忽略外泄漏的影响可得液压缸动态方程：

(3)

式中，Vt—— 伺服阀与液压缸之间管道及液压缸总容积

βe—— 油液的有效体积弹性模量

Ct—— 压力引起的液压缸总内泄漏系数

pL—— 液压缸两腔压力差,pL=p1-p2

QL—— 负载流量

其与阀芯位移xv的关系为：

(4)

式中，Cd—— 阀口流量系数

w—— 阀口面积梯度

ps—— 供油压力

ρ—— 油液密度

xv—— 阀芯位移，为负值时，表示反向

函数sgn(·)定义为

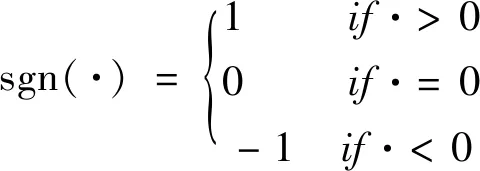
(5)

由于所选用的伺服阀的频宽远高于系统频宽，故可将伺服阀动态简化为一阶环节

τvxv=-xv+kvu

(6)

式中，τv—— 伺服阀时间常数

kv—— 伺服阀增益为正常数

u—— 控制指令

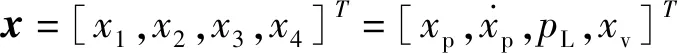
(7)

给定参考运动轨迹为xd(t)，控制目标是设计输入u使得输出y=x1在系统存在不确定性及外部干扰的情况下实现对xd(t)的精确跟踪。

2 控制器设计

2.1 参数化状态空间模型

(8)

假设1：不确定参数及外扰动均有界且满足

θi∈Ωθ=[θiminθimax],i=1,2,3

|d|≤δ

(9)

其中，δ为正常数。从式(8)中可以看出：不确定性存在于状态空间中不包含u的方程中，因此存在未匹配不确定系数，需采用下述反步法解决；函数h实际代表伺服阀的非线性静态增益。

2.2 扩展干扰观测器

基于非线性的扩展状态观测器建立扩展干扰观测器估计不确定参数θ2。

(10)

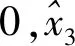
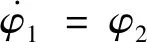
=-β1tanh(β2φ1)-αφ2

(11)

定义李雅普诺夫函数为:

(12)

=β1tanh(β2φ1)φ2+φ2(β1tanh(β2φ1)-αφ2)

(13)

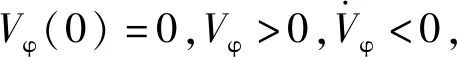
2.3 参数自适应律

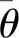
(14)

采用自适应律：

(15)

τ为自适应函数：

τ=φz2

φ=[α1aCx21 0]T

(16)

本研究只对θ1进行估计，θ3由观测器进行估计，α1a由下面(19)式求解。

2.4 自适应鲁棒控制器反步设计

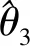
第一步：定义误差变量z1=x1-xd，然后定义滑模面：

(17)

其中，kp为任意正值反馈增益。上述可知，要使误差z1渐进收敛于0，需使z2渐进收敛于0。对式(17)求导并联立式(8)得：

式中，x3为虚拟系统输入，因此针对x3设计一个虚拟控制函数α1以稳定z2：

α1=α1a+α1s

α1s=α1s1+α1s2,α1s1=-k1s1z2

(19)

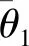
定义虚拟控制函数α1与虚拟控制之间误差变量为z3=x3-α1，将式(19)代入式(18)得：

(20)

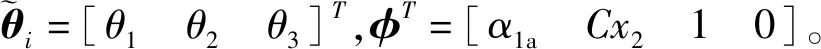
设计αs2并使其满足如下有界条件：

z2α1s2≤0

(21)

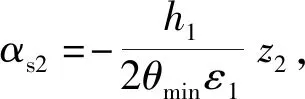
(22)

(23)

第二步：使x3以给定瞬态性能跟踪第一步中设计的α1，即z3=0，根据式(8)定义负载流量QL=h(x3,x4)x4为第三个方程的虚拟输入。针对QL设计控制函数α2，令z4=QL-α2为控制输入偏差。

α2=α2a+α2s

(24)

(25)

定义如下李雅普诺夫函数：

(26)

(27)

α2=α2a+α2s

α2s=α2s1+α2s2,α2s1=-k2s1z2

(28)

式中,k2s1为设计参数大于0。α2s2满足如下有界条件:

z3(α2s2-H)≤ε2

z3α2s2≤0

(29)

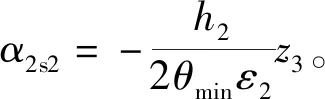
第三步：针对u设计一个实际的控制函数使负载流量QL以给定瞬态性能跟踪第二步中的α2。利用相同的基于李雅普诺夫函数的反推设计方法得:

(30)

定义李雅普诺夫函数如下

(31)

(32)

所以得实际控制函数为:

u=ua+us

us=us1+us2,us1=-k3s1z4

(33)

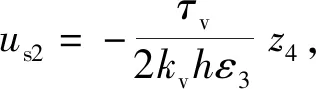
z4us2≤0

(34)

式中,ε3，k3s1为正的设计参数。

控制器控制框图如图3所示。

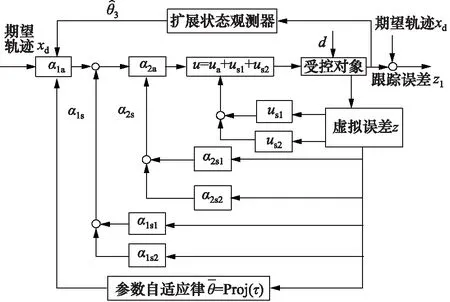
图3 控制框图

3 仿真验证

进行仿真实验以验证基于本研究提出的扩展状态观测器的自适应滑模控制器。设系统参数p1-p2=10 MPa,A1=A2=2.5×10-4m2,τv=kv=0.8,bH=80 N·s/m,Vt=1.5×10-3m3,Cw=0.5，m=100 kg,βe=20 MPa,Ct=8×10-12m5/N·s，控制参数kp=100,k1s1=5,k2s1=3.5,k3s1=3,h1=ε1=1.2,θmax=[70,30,50]T，θmin=[50，-20，-30]T，系统的参考输入信号由MSS海洋模拟工具包生成。采用AMESim与MATLAB联合仿真的形式，将本研究提出的ESOARC控制器与传统PID控制器对比，以验证提出的控制器的性能。

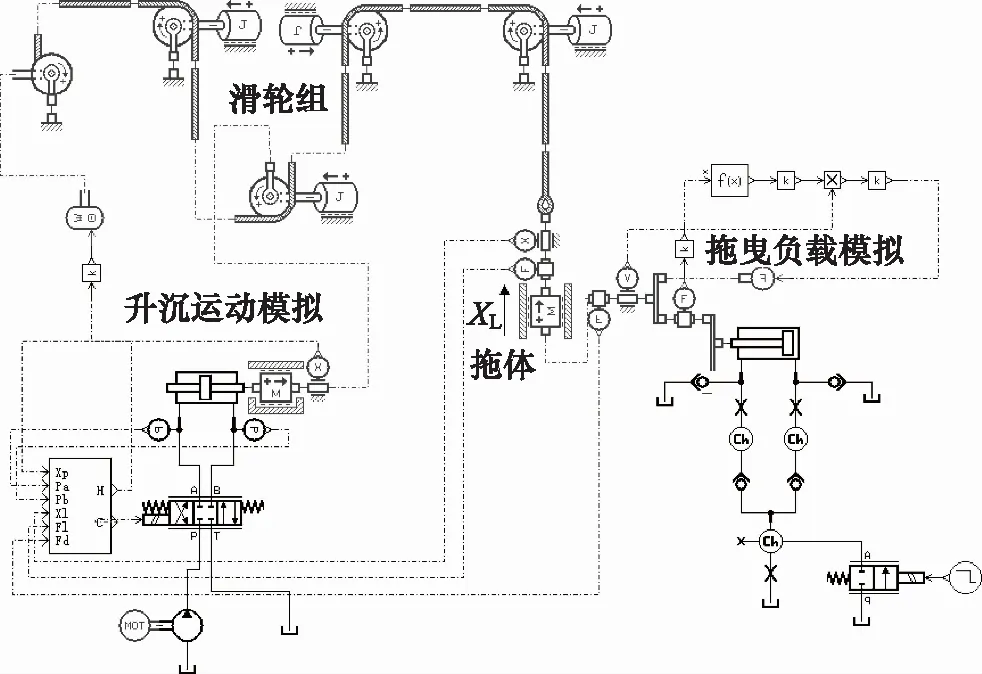
图4 AMESim模型

AMESim和Simulink模型如图4、图5所示。

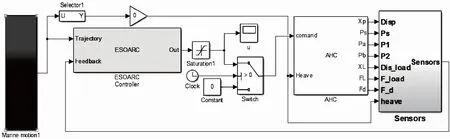
图5 Simulink控制模型

仿真结果如图6所示。由图6可知，本研究提出的ESOARC相比PID控制器具有更好的控制效果。对比2个控制器的稳态误差可知，ESOARC的稳态误差远小于PID控制器的稳态误差。 对于AHC系统而言，2个控制器的相位滞后差别不大，主要差别在于对于参考输入的幅值跟踪上。由于参考输入信号模拟真实海浪，其周期性较弱。从图6b中可以看出在模拟海浪幅值有较大变动的时候，PID控制器的稳态误差明显增大，以致无法满足系统有效补偿升沉运动的需求。如图6a所示，ESOARC控制器稳态误差始终保持在较小的范围内，说明了ESOARC控制器的鲁棒性强于PID控制器。图6d为基于扩展状态观测器的干扰估计曲线，可以看出估计值渐进地收敛于干扰的真实值。

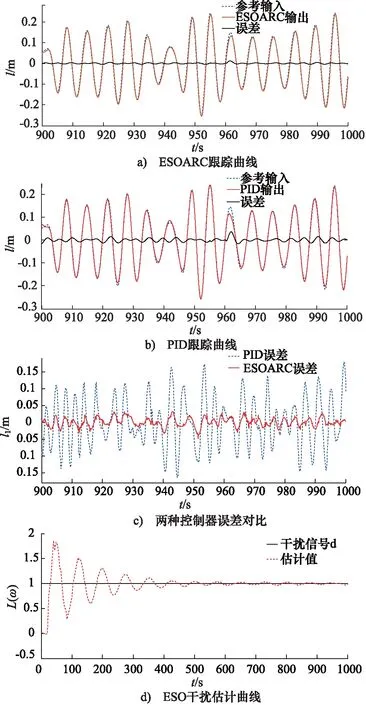
图6 仿真结果

4 结论

(1) 针对复杂多变的海上环境以及电液系统本身的强非线性和不确定性，结合自适应控制和鲁棒控制的优点设计了自适应鲁棒控制器，相比传统PID控制器性能有明显提升。反步法很好解决了系统中未匹配不确定的问题。离散映射方法则解决了自适应控制在于鲁棒控制结合时参数发散的问题。

(2) 基于扩展状态观测器的干扰估计不需要任何干扰的模型信息，避免了传统观测器对噪声模型敏感的问题。