粒子群优化BP算法在温室农作物所需空气湿度中的应用

郭丽丽，刘 勇，*，令狐琛，孙海洋

(1.黑龙江大学 电子工程学院，哈尔滨 150080，2.黑龙江东部节水设备有限公司，黑龙江 绥化 150000)

0 引 言

本文提出将改进的粒子群算法与BP神经网络结合，将其应用在农作物空气湿度的预测中。1986年，Rumelhart等[1]提出了BP神经网络算法，系统地解决了多层神经网络中隐单元连接权的问题，并在数学上给出了完整的推导，同时也得到了广泛的应用，但是基于梯度下降的BP算法存在容易陷入局部极值、收敛速度慢等无法克服的缺陷；1995年美国学者Kennedy等[2]提出的粒子群优化算法PSO引入神经网络的训练当中，受到了研究者们的广泛关注；邱曾帅[3]对温室大棚的空气湿度通过建立数学模型，应用非线性控制理论中输入输出精确状态反馈线性化处理；宋晓萌[4]将物联网技术、模糊PID控制引入到草莓温室大棚环境监控系统中,从低成本、精准控制、操作简便等方面入手,实现草莓温室大棚的智能监控；王耀东[5]提出构建了基于改进粒子群神经网络的地震预测模型，采用了惯性权重和学习因子动态调整策略平衡算法，得到了较低的平均误差率；张二梅[6]从弹药贮存可靠性的特点出发，建立了粒子群与神经网络结合的预测模型，该方法加入了动量项和变学习率参数，实现了弹药贮存可靠性评估与预测的功能；李松等[7]人提出了改进粒子群算法优化BP神经网络的短时交通流预测，在算法中加入自适应变异算子，对实测交通流具有更好的非线性拟合能力和更高的预测精度；郑玲[8]提出了基于神经网络的电影票房预测模型，引入遗传算法优化BP神经网络的权值和阈值，实验结果平均绝对误差低于15%，预测效果良好。

本文将PSO算法中的惯性权值进行改进，与BP算法结合应用在农作物空气湿度的预测中，目的是通过智能算法控制农作物不同生长时期对空气湿度的需求，Korner等[9]和王佳琦等[10]的研究表明温室内湿度的变化会影响生农作物的生长状态与产量，在湿度很高的情况下，农作物容易被真菌病害所腐蚀，直接影响农作物的质量和产量，相反湿度过低的情况下，会造成农作物的严重失水而导致作物生长不良甚至死亡，所以对空气湿度的有效控制是必要的，而且大棚内空气温度和湿度具有一定的耦合关系，在把空气温度稳定的情况下，将BP智能算法运用到空气湿度中。

1 BP神经网络

BP(反向传播)神经网络即输入信号正向传播、误差反向传播，此过程不断迭代，最后使得误差信号减小到更接近期望值。BP神经网络具有很强的非线性逼近能力、并行分布式处理能力、自学习和自适应能力等特性，受到了广泛的使用[11-12]。设输入层有n个单元，网络的输入模式为x=(x1,x2,…,xn)T，隐含层有h个单元，隐含层的输出为y=(y1,y2,…,yh)T，输出层有m个单元，输出为z=(z1,z2,…,zm)T，目标输出为t=(t1,t2,…,tm)T，隐含层到输出层的传递函数为f，输出层的传递函数为g，可得：

(1)

式中yj为隐含层第j个神经元的输出，w0j=θ,x0=-1

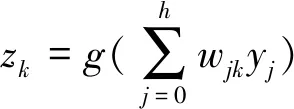
(2)

式中zk为输出层第k个神经元的输出，此时网络输出和目标输出的误差为：

(3)

然后进行权值和阈值的不断调整，使ε值减小。

wjk(t+1)=wjk(t)+ηδkyj

(4)

上式为隐含层到输出层的权值调整迭代公式:

wij(t+1)=wij(t)+ηδjxi

(5)

上式为输入层到隐含层的权值调整迭代公式。

2 改进粒子群优化算法

虽然BP算法已被广泛应用，然而，基于梯度下降的BP算法存在容易陷入局部极值、收敛速度慢等无法克服的缺陷，因此，一个全局优化的算法自然而然地被引进到神经网络的训练中，PSO粒子群算法的计算速度快且算法本身涉及的参数少，这种算法被广泛地应用于各个领域，所以在解决实际问题中展示了其优越性。为了更好地提高算法的收敛速度和精度，本文还提出了非线性权值递减策略，试验结果表示效果最佳[13-14]。

假设在一个维度为d的目标空间，粒子群的个数为n，则粒子群中第i个粒子的位置和速度均可用一个d维向量表示，

Xi=(xi1,xi2,…，xid)

(6)

Vi=(vi1,vi2,…，vid)

(7)

为了平衡算法全局搜索和局部搜索能力，解决算法收敛度不高且已陷入局部极值的缺点，1998年，Shi等[15]将惯性权重引入PSO算法，对粒子群算法进行了改进，该算法能够保证较好的收敛效果，进化过程：

Vij(t+1)=wVij(t)+c1r1[Vij(t)-Xij(t)]+c2r2[Pgj(t)-Xij(t)]

(8)

Xij(t+1)=Xij(t)+Vij(t+1)

(9)

其中i=1,2，…，n,j=1,2，…，d,n为粒子群中粒子的数量，d为目标空间的维度;c1和c2为学习因子;r1和r2均为随机数，取值范围为[0,1]；w为惯性权重，式(8)中第一部分为粒子先前的速度，用于保证全局收敛性；第二、三部分则使算法具有局部收敛能力。可以从式(8)看出惯性权重w为在多大程度上保留原来的速度：w较大，则全局收敛能力较强；w较小，则局部收敛能力较强。

标准粒子群算法常用的是Shi等人提出的线性递减权值策略表达式：

(10)

搜索过程是一个非线性的复杂过程，本文将线性递减权值策略改成非线性递减权值策略，来增强局部和全局的搜索能力，可以表示为：

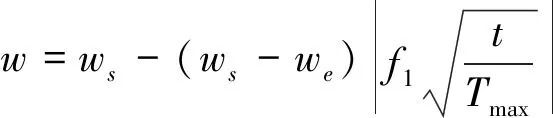
(11)

其中，Tmax为最大进化代数；ws为初始惯性权重值，we为进化到最大允许迭代次数的惯性权重，t为当前迭代次数，f1为控制因子，取ws=0.95，we=0.4。当t=0时，函数值等于初始权值ws，当t=Tmax时，f1取不同的值会得到不同的下降效果，f1取值较大时会使w在算法早期较快减小到接近we，迫使算法早期陷入局部搜索；取值较小时，会使得t=Tmax时，w仍远大于we，经实验测试f1取值为0.9时，实验效果最好，本文中f1取值为0.9，实验结果表示该改进策略可以较好的维护全局搜索和局部搜索的平衡。

3 粒子群BP神经网络结合原理

3.1 粒子群算法优化BP神经网络的算法步骤

1)初始化参数：BP神经网络拓扑结构，粒子个数n=30，粒子维数d=21，最大迭代次数Tmax=1 000，学习因子c1=c2=2，惯性权重ws=0.95、we=0.40，学习率lr=0.05，目标误差goal=0.000 1,粒子的最大速度vmax=1和最小速度vmin=-1等参数。

图1 整体算法流程图Fig.1 Overall algorithm flow chart

3)根据式(8)和式(9)更新每个粒子的速度与位置，并判断更新后粒子的速度与位置是否在限定范围内。

4)检查算法迭代停止条件，若结果理想，则停止迭代输出BP神经网络的权值或阈值，使得BP网络更好地减小误差，否则转步骤2)。

算法流程见图1。

3.2 粒子群优化算法与神经网络仿真分析

以黑龙江省绥化市大棚温室草莓的种植为例，研究大棚内草莓不同生长时期的空气湿度需求。草莓的开花期对空气湿度比较严格，湿度过大过小都会造成授粉不良，此时空气相对湿度控制在40%左右；草莓的保温初期为防止草莓进入休眠期，需要的温度相对高一些，此时空气相对湿度控制在85%～90%；草莓的果实膨大和成熟期，受温度影响较大，湿度可控制在60%～70%。

根据这些控制要求，本文以草莓开花期的空气湿度做试验，用优化的智能算法来控制，构建了一个3层BP神经网络应用到大棚空气湿度的预测中，其中输入层节点为2个，隐含层节点为5个，隐含层的激活函数为‘tansig’，输出层节点为1个，输出层激活函数为‘logsig’。应用中把太阳光照和棚内空气温度两个参数作为输入变量，草莓所需要的的最适宜空气湿度作为输出变量来进行仿真测试，仿真试验选取了冬季温室草莓的30个数据，前20个数据为训练数据，后10个数据为测试数据，为了更好地体现结果的优良值，将BP网络算法、线性PSO-BP网络算法和非线性PSO-BP网络算法的结果进行对比，仿真结果见图2～图4。3种算法的平均误差率见表1。

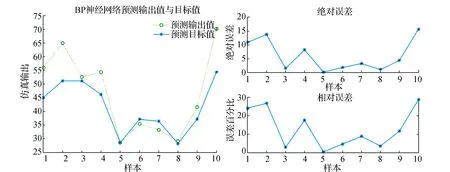
图2 BP网络预测输出和目标输出相关误差图Fig.2 Error map between BP network prediction output and target output

图3 线性 PSO-BP网络预测输出和目标输出及相关误差图Fig.3 Error map between linear PSO-BP network prediction output and target output

图4 非线性PSO-BP网络预测输出和目标输出及相关误差图Fig.4 Error map between nonlinear PSO-BP network prediction output and target output

由表1可见，非线性PSO优化后的BP神经网络在训练误差上比其他2种算法小很多，表明非线性PSO-BP算法具有很强的学习能力和泛化能力；由图4和表1可见，传统BP容易陷入极值尤其是样本的目标输出值超过了预测输出值，误差率也是3种算法最高的；线性PSO-BP网络和非线性PSO-BP网络整体看训练效果相近，但非线性PSO-BP网络比线性的误差率小，非线性PSO-BP网络训练效果最好；非线性PSO-BP网络相对误差最小，精确度最高，全局搜索能力也较好。综上所述，本文提出的优化方案是可行的。

表1 3种算法平均误差率比较

4 结 论

针对农业种植空气湿度的预测，本文提出了用粒子群算法PSO优化BP神经网络的智能优化算法。该算法融合了种群活动机制与反向传播神经网络的思想，在一定程度上提高了算法的全局搜索能力、收敛精度和速度，这样以便较快地控制农作物不同生长时期对空气湿度的需求，使农作物拥有一个较好的生长环境。