多Euler-Lagrange系统有限时间跟踪控制
林晓涵, 史小平,*, 邹世琦,李师轮
(哈尔滨工业大学 a. 控制与仿真中心;b. 航天学院,哈尔滨 150001)
0 引 言
在多智能体协同飞行控制中,目标跟踪控制在近年得到了国内外学者广泛的关注和研究。而多Euler-Lagrange系统可求解较复杂的非线性质点系统,且具有表达式简洁、应用时只需计算系统的动能和广义力[1-4]等优点,被应用于无人机[5]、航天器编队飞行[6]、机械臂[7]等非线性物理系统。因此基于Euler-Lagrange动力学模型的多智能体系统跟踪控制具有明显的通用性和研究意义[8]。
多Euler-Lagrange系统跟踪控制问题是多智能体协同控制中重要的组成部分,具有实际的应用意义和研究前景,目前主要的研究方法包括自适应控制[9]、复杂逻辑控制[10]、H∞控制[11]等,其中滑模控制因其结构简单、响应速度快、强鲁棒性的优点被应用解决多Euler-Lagrange系统控制问题。文献[12]在系统存在模型不确定性和外界干扰的情况下,选取合适的有限时间滑模变量,提出了分布式有限时间包含跟踪控制算法。文献[13]考虑多Euler-Lagrange系统在含有障碍物情况下的跟踪控制问题,并基于改进的非奇异终端滑模面设计了有限时间控制算法,使跟踪误差有限时间内收敛到目标位置。然而,在实际应用中由于所提出的控制律具有不连续性等特点,滑模控制会引起不可忽略的抖振现象,因此高阶滑模控制的提出既保留了经典滑模控制的优点,又提高了系统的控制精度和控制性能。文献[14]基于超分观测器对具有干扰的二阶积分系统设计了连续的控制器。文献[15]在考虑外部干扰和内部不确定性的情况下,对航天器非线性系统的姿态跟踪控制设计了有限时间二阶滑模控制算法,并引入线性修正项提高闭环系统的动力学性能。
在多Euler-Lagrange系统的跟踪过程中,为了快速完成控制目标任务,使系统在有限时间内收敛到平衡点,所以有限时间控制具有重要而有效地工程应用意义。文献[16]考虑输入饱和且存在误差约束的情况下,为含有不确定性的多Euler-Lagrange系统设计了分布式有限时间跟踪控制律,并利用神经网络对系统未知项进行实时在线补偿。文献[17]进一步考虑速度信息无法测量的情况下,利用齐次性原理为系统设计了分布式有限时间跟踪控制算法,实现了对期望目标的跟踪控制。文献[18]引入一阶和二阶分布式滑模估计器分别保证在有限时间内对速度和位置准确地估计,并提出相应的有限时间分布式编队控制算法,实现多智能体系统有限时间跟踪控制。
上述文献都只考虑了某一部分的作用情况,而对于考虑出现抖振现象的多Euler-Lagrange系统协同跟踪控制则很少考虑。由于引入非奇异终端滑模面所得到的控制器避免抖振现象的出现,且超螺旋滑模可以避免抖振现象的发生。因此本文利用非奇异终端滑模面与超螺旋算法相互结合,实现有限时间跟踪控制的目的。在本文中首先提出相应代表系统智能体数学描述的多Euler-Lagrange系统方程,并对有限时间理论的相关引理进行分析;其次,选取合适的非奇异终端滑模面,并结合超螺旋滑模控制提出了一个超螺旋非奇异终端滑模有限时间控制器,通过选取合理的Lyapunov函数方法,证明了多Euler-Lagrange系统有限时间收敛。最后,通过仿真结果表明本文所提出方法能够有效地实现控制目标。
1 数学基础和问题描述
1.1 多Euler-Lagrange系统模型
本文假设多Euler-Lagrange系统由n个智能体组成,其中第i个智能体的动力学模型为:
(1)

在本文中,多Euler-Lagrange系统满足以下假设和性质:


(2)
性质3多Euler-Lagrange系统模型不确定性和干扰是有界的:
(3)
其中dm为已知常量。
定义Euler-Lagrange系统的跟踪误差向量为e=q-qd=[e1,…,en]T,其中qd∈Rn为期望跟踪轨迹,根据式(1)可得到跟踪误差动力学模型:
(4)

1.2 相关引理
考虑系统如下形式:

(5)
其中f:U0→Rn为定义在x=0的开邻域U0∈Rn上的一个连续函数。
引理 1[19]对于系统(5),若存在一个连续可微的正定函数V(t),使如下微分不等式成立:

(6)
其中λ1为正实数,σ∈(0,1),则原点为系统的局部有限时间平衡点,且收敛时间t满足如下不等式:

(7)
其中x0为系统状态的初始值。
2 控制器设计
控制目标:针对多Euler-Lagrange系统有限时间的跟踪控制问题,提出适合系统的非奇异终端滑模面,并引入连续超螺旋高阶控制项,设计了基于超螺旋高阶的非奇异终端滑模控制方法,使多Euler-Lagrange系统能够消除抖振现象的发生,同时在有限时间内实现对期望目标的跟踪。
选取非奇异终端滑模面为:

(8)
其中s(t)=[s1,s2,…,sn]T,α,β>0为已知常量参数。

证明1:若s(t)=0,式(8)可以写为:

(9)
选取如下Lyapunov函数:
(10)
对式(10)关于时间求导:
(11)

为实现控制目标,本文采用超螺旋滑模提出了一个超螺旋非奇异终端滑模有限时间控制器,其特点是有限时间收敛且无抖振现象。
基于超螺旋非奇异终端滑模控制方法,设计相对应控制要求的控制器:

(12)
(13)


(14)
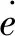
证明2:由式(8)可知:
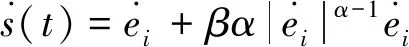
(15)
将控制器式(12)、式(13)代入式(15)可得:

(16)
选取Lyapunov函数为:
V2(t)=θTΓθ
(17)
其中:
(18)

(19)
定义向量空间如下:Θ={(s,γ)∈Rn:s=0}。
则由分析可知,Lyapunov函数V2(t)在空间Θ正定且无界,满足:

(20)

对上式Lyapunov函数关于时间求导:
(21)
其中:
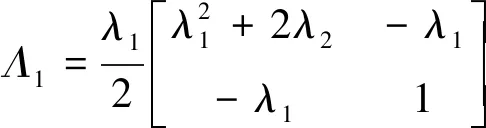
(22)

(23)
则:

(24)
其中:

(25)
经过计算证明可知,若式(14)成立,且式(25)中满足Λ>0,则V2(t)非负正定。
由式(20)可得:

(26)

(27)
联立式(26)、式(27),代入式(24)可得:

(28)
其中:

(29)


(30)

3 仿真分析
本节对含有多Euler-Lagrange系统的航天器编队飞行系统进行相关的仿真分析,并验证所提出控制律的准确性和有效性。
选取具有代表性的航天器编队飞行系统,利用修正罗德里格参数来描述编队飞行中第i颗航天器的姿态运动学和动力学模型,如下所示:

(31)

(32)

根据上述分析,可将式(31)和式(32)联立并转换为Euler-Lagrange方程形式:
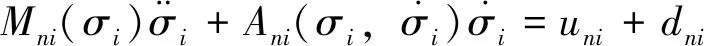
(33)
其中:
Mni(σi)=G-T(σi)JiG-1(σi)
(34)

(35)
uni=G-T(σi)ui
(36)
dni=G-T(σi)di
(37)
在仿真过程中,考虑3颗航天器编队飞行的相应情况,设置相应参数如下,航天器转动惯量矩阵分别为:J1=[10,0.5,0.5;0.5,10,0.5;0.5,0.5,10]Tkg·m2,J2=[15,0.5,0.5;0.5,15,0.5;0.5,0.5,15]Tkg·m2,J3=[10,0.6,0.6;0.6,10,0.6;0.6,0.6,10]Tkg·m2;航天器初始角速度均为:ωi(0)=[0,0,0]Trad/s;航天器初始姿态角分别为:σ1(0)=[0.05,0.05,-0.05]T,σ2(0)=[0.05,-0.05,0.05]T,σ3(0)=[-0.05,0.05,0.05]T。航天器所受到的外部扰动为:di=0.05[sin(0.5t),cos(0.5t),sin(0.5t)]TN·m。所设计控制器中的各项参数设定为:λ1=8,λ2=6。
在控制器式(12)、式(13)作用下的相对控制力变化曲线、相对姿态跟踪误差变化曲线、相对角速度跟踪误差变化曲线分别见图1、图2、图3。根据仿真结果可见,航天器编队飞行系统能够实现在有限时间内对期望状态轨迹的协同跟踪控制,且姿态和角速度跟踪误差均趋近于零。并且在初始阶段控制力存在较大幅度的振荡,当航天器编队飞行系统的姿态和角速度跟踪误差均趋于收敛时,控制力变化可以保持在较小范围振荡,由此可见,航天器编队飞行系统可在有限时间跟踪控制目标,且具有较快的收敛跟踪性能和较为准确的控制跟踪精度。

图1 航天器编队飞行系统相对控制力变化曲线Fig.1 Diagram of the relative control input for spacecraft formation flying system
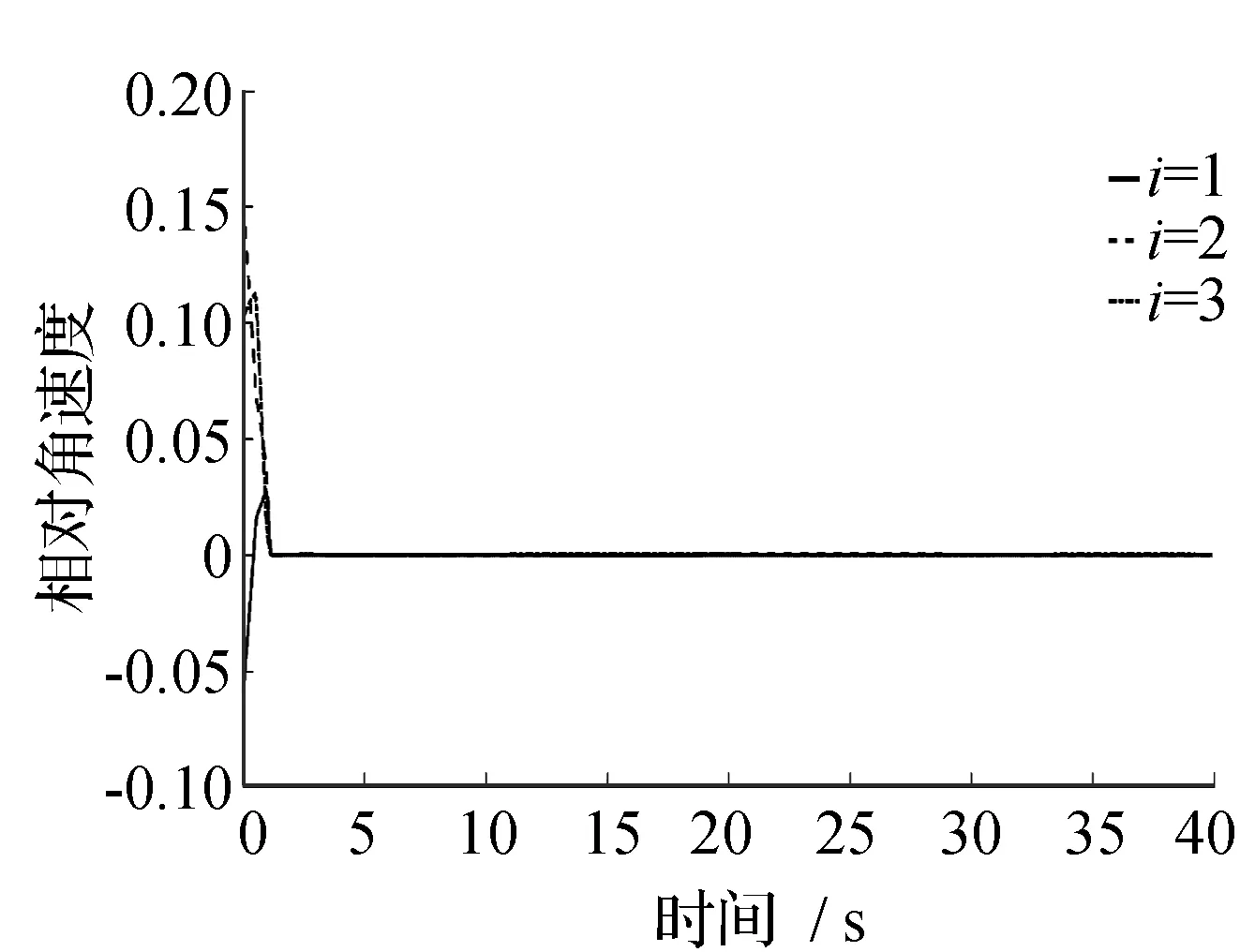
图3 航天器编队飞行系统相对角速度变化曲线Fig.3 Diagram of the relative angular velocity for spacecraft formation flying system

图2 航天器编队飞行系统相对姿态变化曲线Fig.2 Diagram of the relative attitude for spacecraft formation flying system
4 结 论
本文针对多Euler-Lagrange系统进行有限时间协同跟踪控制。分析建立多Euler-Lagrange系统跟踪动力学误差模型,并通过引入连续超螺旋控制算法,与所提出的非奇异终端滑模面相互结合,在所设计的控制器作用下,多Euler-Lagrange系统能够消除抖振现象的发生,并完成有限时间跟踪期望目标的要求。通过仿真结果验证了本文所提出控制器的合理性和有效性,为后续针对存在扰动影响的多Euler-Lagrange系统具有一定的启发性和研究基础。

