具有水平流动的混合流体对流的扰动方程组

宁利中，张 迪，宁碧波，田伟利

(1.西安理工大学 水利水电学院，西安 710048； 2.嘉兴学院 建筑工程学院， 浙江 嘉兴 314001；3.上海大学 建筑系， 上海 200444)

0 引 言

从底部加热的两平板之间的自然对流，即Rayleigh-Benard对流，是研究流动稳定性和对流时空特性的模型之一。自1900年开始研究Rayleigh-Benard对流以来，研究工作取得了很大进展[1-2]。随着计算机的出现，数值模拟已成为主要的研究手段之一。文献[3-12]混合流体对流的流体力学基本方程组的数值模拟，研究了混合流体对流中的定常波，行波，局部行波形成，缺陷形成及其时空结构与非线性动力学特性等。对传统的Rayleigh-Benard对流模型系统施加一个水平流动，或者说，对于水平流动问题从底部施加一个热作用，这样，形成一个新的对流模型系统，即具有水平流动的Rayleigh-Benard对流问题。文献[13-18]通过具有水平流动的单流体Rayleigh-Benard对流问题的流体力学基本方程组的数值模拟，研究了单流体对流中边界条件与进口对对流斑图的影响，局部行波特性及对流斑图的分区等。文献[19-24]通过具有水平流动的混合流体Rayleigh-Benard对流问题的流体力学基本方程组的数值模拟，研究了混合流体对流中周期变化的局部行波结构，充分发展的行波结构及水平流动对对流斑图的影响。这些工作都是基于流体力学基本方程组进行的。扰动方程组一般被使用在流动稳定性分析中获得对流发生的临界值。可是，文献[25-29]通过混合流体Rayleigh-Benard对流问题的流体力学扰动方程组的数值模拟，获得了混合流体对流中的扰动的成长，对流的行波结构，局部行波结构，对传波结构及其时空结构与非线性动力学特性等。文献[30-34]在Rayleigh-Benard对流问题研究中获得了某些进展。因此，为了用扰动方程组研究具有水平流动的Rayleigh-Benard对流问题，有必要对具有水平流动的Rayleigh-Benard对流问题的扰动方程组进行推导与研究。从而推动Rayleigh-Benard对流问题的深入研究。

本文讨论了混合流体对流的流体力学方程组和扰动方程组。基于布辛涅斯克近似，给出了考虑Soret效应和Dufour效应的混合流体对流的基本方程组。对于混合液体在忽略Dufour效应的情况下，推导了具有水平流动的混合流体对流的扰动方程组。应用扰动方程组可以计算具有水平流动的混合流体对流的稳定性和对流时空结构特性。如果忽略扰动方程组中二阶以上的高阶项，方程组可简化成线性稳定分析的扰动方程组。

1 流体力学基本方程组

考虑在均匀重力场下从下面加热的流体混合物水平层的对流问题(图1)。当瑞利数超过临界值时，发生对流运动。假设系统是一个忽略了滚动轴向变化的二维对流滚动。坐标的原点位于腔体中底板与左端壁以直角相交的点上，x，z表示垂直于滚动轴线的笛卡尔坐标，z轴朝上为正，x轴朝右为正。在布辛涅斯克近似的框架内，描述系统的基本方程可以写成：

▽·U=0

(1)

(2)

(3)

(4)

式中▽为梯度算子；▽2为Laplace算子；U(U,0,W)，T，C，p*，ρ，ν,g，Cp,τ分别为速度矢量，温度，浓度，压强，密度，运动黏性系数，重力加速度，比热，时间，下标0表示相应物理量的参考值；Jc为物质通量；q为热通量。Jc和q可根据Onsager的线性非平衡热力学理论确定[35-36]，即：

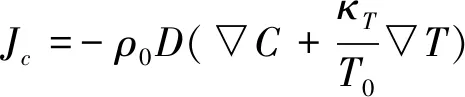
(5)

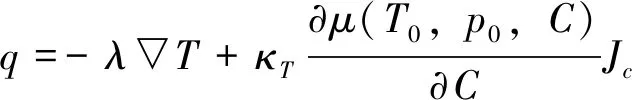
(6)

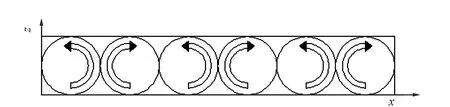
图1 对流示意图Fig.1 Convection schemetic diagram

式中κT，λ，D分别为与Soret效应有关的系数、导热系数和浓度扩散系数；μ为混合物的局部化学势。笔者简单地描述Soret效应和Dufour效应。它们发生在一个力学平衡的非等温流体系统中。对于具有扩散系数D>0的混合物的流体层，当在溶液中几乎瞬间建立稳定的温度梯度时，热扩散产生组分的浓度梯度，从而使该组分的扩散通量与热扩散方向相反。一段时间后，热扩散和反扩散将完全平衡，整个系统将达到一个稳定状态。因此，在这个系统中，浓度梯度是由温度梯度决定的。这种现象称为Soret效应。它已经反映在物质通量Jc的表达式中，即式(5)右侧的第二项。Soret效应的逆现象是Dufour效应，它是浓度梯度导致的温度梯度的形成。它已经反映在热通量q的表达式中，即式(6)右侧的第二项。

考虑温度T，浓度C离开参考值偏差很小，质量密度的状态方程为:

ρ=ρ0[1-α(T-T0)-β(C-C0)]

(7)

式中恒压和恒浓度下的热膨胀系数α和恒温和恒压下的溶质膨胀系数β定义为:

重力场g平行于z轴，方向向下，g=-gez，ez为z轴方向的单位矢量。代物质通量Jc，热通量q和密度ρ到方程(1)～(4)，得：

▽·U=0

(8)

(9)

(10)

(11)

2 无因次流体力学基本方程组

对方程(8)～(11)中的所有物理量用腔体高度d，热扩散率κ，参考密度ρ03个基本量无因次化。选用热扩散率κ同样包含时间的因素。选用热扩散率κ更好的反映了热对流中的热扩散特性。考虑Soret效应和Dufour效应的无因次形式的混合流体对流基本方程组可表示为:

▽·δU=0

(12)

(13)

(14)

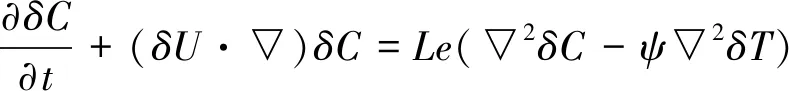
(15)

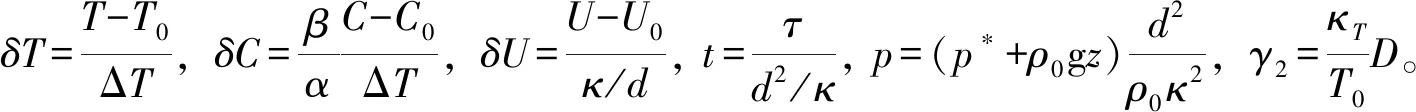
为了计算方便，浓度流δζ被定义为：

δζ=δC-ψδT

(16)

无因次形式的混合流体对流基本方程组可表示为：

▽·δU=0

(17)

(18)

(19)

(20)

方程(17)～(20)是考虑Soret效应和Dufour效应的无因次形式的混合流体对流基本方程组。Dufour效应发生在混合气体中，因此，对于混合气体，Dufour效应项必须保留，但对于混合液体，Dufour效应项可以忽略，Soret效应项必须保留。下面讨论混合液体的对流问题，忽略Dufour效应项后，无因次形式的混合流体对流基本方程组可表示为：

▽·δU=0

(21)

(22)

(23)

(24)

方程(21)～(24)是考虑Soret效应的无因次形式的混合流体对流基本方程组。利用流体力学基本方程(21)～(23)，文献[3-12]模拟了混合流体对流的时空结构和动力学特性，文献[19-24]模拟了具有水平流动的混合流体对流的时空结构和动力学特性。在方程(21)～(24)简化成单流体对流方程组后，文献[13-18]模拟了具有水平流动的单流体对流的时空结构和动力学特性。

3 流体力学基本方程的传导解

考虑具有水平流动的混合流体对流系统，对流未发生时方程(21)～(24)的传导解为：

δUcond=4RePrz(1-z)ex

(25)

δTcond=0.5-z

(26)

δCcond=ψ(0.5-z)

(27)

δζcond=0

(28)

(29)

4 流体力学扰动方程组

4.1 具有水平流动的混合流体对流扰动方程组

如果对流发生，离开传导解的扰动量可表示为：

u=δU-δUcond

(30)

θ=δT-δTcond

(31)

ξ=δC-δCcond

(32)

p′=p-pcond

(33)

η=δζ-δζcond

(34)

式中u=(u,0,w)，代扰动量定义式(30)～式(34)到方程(21)～(24)，具有水平流动的混合流体对流扰动方程组可表示为:

▽·u=0

(35)

(36)

(37)

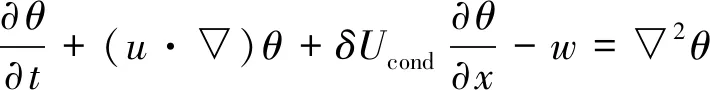
(38)

(39)

式中δUcond=RePrz(1-z)。扰动方程(35)～(39)是非线性的，可以直接用于具有水平流动的混合流体对流的稳定性，扰动成长，对流时空结构与动力学特性的分析。如果忽略扰动方程组中二阶以上的高阶项，即非线性项，可得具有水平流动的混合流体对流的线性稳定分析所依据的扰动方程组。

4.2 混合流体对流扰动方程组

考虑方程(35)～(39)中的水平流动δUcond=0，可得混合流体Rayleigh-Benard对流的扰动方程组，即：

▽·u=0

(40)

(41)

(42)

(43)

(44)

方程(40)～(44)与文献[25-29]在混合流体Rayleigh-Benard对流时空结构与动力学特性分析中采用的扰动方程组一致。只是无因次化时本文采用了d，κ，ρ03个基本量，文献[25-29]采用d，ν，ρ03个基本量。由于基本量选择的不同，方程的形式稍有不同而已。

4.3 具有水平流动的单流体对流扰动方程组

忽略方程(39)，考虑方程(35)～(38)中的分离比ψ=0，扰动浓度流η=0，可得具有水平流动的单流体Rayleigh-Benard对流的扰动方程组，即：

▽·u=0

(45)

(46)

(47)

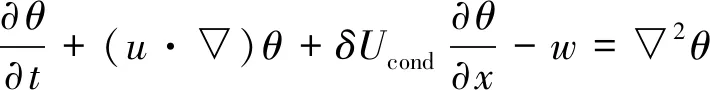
(48)

4.4 单流体对流扰动方程组

忽略方程(38)，考虑方程(35)～(38)中的分离比ψ=0，扰动浓度流η=0，水平流动δUcond=0，可得单流体Rayleigh-Benard对流的扰动方程组，即：

▽·u=0

(49)

(50)

(51)

(52)

4.5 水平流动问题的扰动方程组

忽略方程(38)～(39)，考虑方程(35)～(37)中的分离比ψ=0，扰动浓度流η=0，扰动温度θ=0，可得单流体水平流动问题的扰动方程组，即：

▽·u=0

(53)

(54)

(55)

方程(53)～(55)与文献[38]采用的单流体水平流动问题的扰动方程组一致，只是无因次化时采用的基本量不同，方程的形式稍有不同而已。

上述4.2-4.5节中的扰动方程组是非线性的，可以直接用于对流稳定性和对流特性的分析。如果忽略二阶以上的高阶项，即非线性项，就可以获得线性稳定分析所依据的扰动方程组。

5 结 论

本文讨论了具有水平流动的混合流体对流的流体力学方程组和扰动方程组。基于布辛涅斯克近似，给出了考虑Soret效应和Dufour效应的混合流体对流的基本方程组，给出了基本方程组的无对流运动的传导解。对于混合液体在忽略Dufour效应的情况下，推导了具有水平流动的混合流体对流的扰动方程组。根据不同的简化条件，前述扰动方程组可以应用于具有水平流动的单流体对流问题，混合流体对流问题，单流体对流问题，或者单流体水平流动问题等情况。本文建议的扰动方程组可以应用于相应条件的对流稳定性分析及对流时空结构与动力学特性的模拟。