对2019年北京理科导数题的一种解法探究与推广
湖北省恩施州教育科学研究院
高考题的设问和解法往往具有基础性,思维的启迪性!因此研究高考题肯定避免不了研究其解法,把高考题作为例题进行选讲,要充分发挥它解法的基础性、示范性、典型性[1].因此复习备考中很有必要提炼高考题中解法的典型性和通性,甚至有时候一道试题的命制就是基于这种解法的通性.
一、问题的提出与思考
例1(2019年高考北京卷理科第19题)已知f(x)=
(1)求曲线y=f(x)的斜率为1的切线方程;
(2)当x ∈[-2,4]时,求证:x-6≤f(x)≤x;
(3)设F(x)=|f(x)-(x+a)|(a ∈R),记F(x)在区间[-2,4]上的最大值为M(a),当M(a)最小时,求a的值.
解(1)由题意得解得因为所以对应的切点分别为(0,0)或所以切线方程为y=x或
(2)设g(x)=f(x)-x,则所以g(x)在上单调递增,在上单调递减.因为g(-2)=-6,g(0)= 0,所以当x ∈[-2,4]时,-6≤g(x)≤0,即x-6≤f(x)≤x.
(3)由(2)知x-6≤f(x)≤x,又F(x)=|f(x)-(x+a)|≤M(a)恒成立,所以有x+a-M(a)≤f(x)≤x+a+M(a),所以所以M(a)≥3,当取最小值时可得a=-3.
从例1的解答来看,步步为营,思维和设问十分具有层次性.那么:
问题1为什么例1 第(1)问要求y=f(x)的斜率为1的切线方程?
问题2为什么例1 第(2)问要选取区间[-2,4]?
问题3第(3)问中若令h(x)=x+a,h(x)的斜率也是1,是巧合吗?
问题4若h(x)=kx+a,此时F(x)=|f(x)-(kx+a)|(k,a ∈R)在区间[-2,4]上的最大值的最小值又当如何?
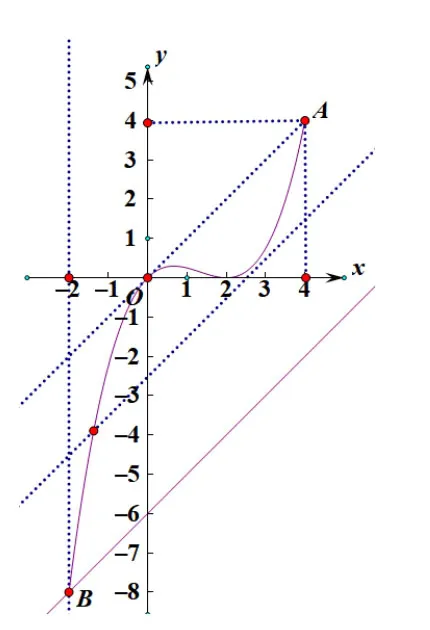
图1
对于前面两个问题不难回答,我们只要利用数形结合思想,画出函数图像就能很快得到答案,如图1,y=f(x)在x ∈[-2,4]时图像恰好被y=x-6与y=x两条斜率为1的平行线“夹逼”.不难看出,这两条“夹逼”平行线的位置主要是由图像上三个关键点(两端点和切点)确定! 因此第(1)问就是为后面第(2)问作铺垫!至于此题中区间[-2,4]选取最关键的还是右端点,因为点A坐标为(4,8),AO恰好是曲线的一条切线!而区间左端点却是可以变化的,只是会影响第(3)问的结果.问题3中第(3)问中h(x)的斜率也是1,这其实是命题者设置的“巧合”,因为若h(x)=kx+a,此时F(x)=|f(x)-(kx+a)|(k,a ∈R)在区间[-2,4]上的最大值取最小时恰好k=1.下面我们主要探讨问题4中这种最大值的最小值情形!
二、含双参数时最大值取最小问题的解法
设F(x)=|f(x)-(kx+a)|(k,a ∈R),记F(x)在区间[m,n]上的最大值为M(k,a),此时M(k,a)含有双参数,那么M(k,a)最小值如何取得呢?事实上,这类问题的解答完全可以根据例1 高考题的设问层次与思维方式,找出三个关键点,利用平行线“夹逼”的方式解决.因为基于函数视角,若定义为函数y=f(x)与函数y=kx+m在区间[m,n]上的偏差,那么偏差的几何意义就是两函数图像上纵坐标之差绝对值的最大值.用两平行线“夹逼”函数y=f(x)图像会使得偏差最小.
例2已知函数f(x)=x3+ax+b定义域为[-1,2],记|f(x)|的最大值为M,则M的最小值为
A.4 B.3 C.2 D.1
解析由题意,|f(x)| =|x3-(-ax-b)|≤M在区间[-1,2]恒成立.令g(x)=x3,先找出g(x)图像上的三个关键点.画出g(x)图像(如图2),A(2,8),B(-1,-1),连接AB两点,可求出直线AB的斜率kAB=3,直线AB的方程为y=3x+2,与AB平行直线l与g(x)图像相切于点C,则令g′(x)= 3x2=3,可解得x=±1.所以C(1,1),直线l的方程为y=3x-2,所以3x-2≤x3≤3x+2.又由于-ax-b-M≤x3≤-ax-b+M,所以当a=-3,b=0时Mmin=2,答案选C.

图2

图3

图4
变式已知函数f(x)=x3+ax+b定义域为[-1,1],记|f(x)|的最大值为M,则M的最小值为___.
解析此时只有定义域的范围发生了变化,在找关键点构造平行线“夹逼”时不能再继续选取AB连线,这时要先求过点A(或B)作g(x)=x3图像的切线,如图3,设切点为(t,t3)(t1),那么解得或t=1(舍去),所以那么直线AC的方程为由对称性可得过点的切线BD与AC平行,两平行线“夹逼”g(x)=x3图像,所以又由于-ax-b-M≤x3≤-ax-b+M,所以当时
例1′(例1的变式)已知设F(x)=|f(x)-(kx+a)|(k,a ∈R)在区间[-2,4]上的最大值为M(k,a),求M(k,a)的最小值.
解析如图1,x-6≤f(x)≤x,又kx+a-M(k,a)≤f(x)≤kx+a+M(k,a),所以 当k=1,a=-3时M(k,a)min=3.这就体现了前文说到的例1“第(3)问中h(x)的斜率也是1”是命题者设置的“巧合”.
例3已知函数令g(x)=|f(x)-ax-b|(a,b ∈R),设g(x)的最大值为M(a,b),求M(a,b)的最小值.
解析f(x)的图像如图4,点为f(x)图像两端点,直线AB的方程为与AB平行且与f(x)图像相切的直线必过最低点C(1,2),方程为y=2,所以又由于ax+b-M(a,b)≤f(x)≤ax+b+M(a,b),所以当a=0,时
三、解法推广
类似以上题型还有很多,都可采取这种通过关键的三点(端点、切点)的两条平行线“夹逼”来解决.若设这两组平行线为h1(x)=k0x+b1,h2(x)=k0x+b2,且满足关系式h1(x)≤f(x)≤h2(x),记不难发现,例1中有h1(x)=x-6,h2(x)=x,Mmin=例2中有h1(x)= 3x-2,h2(x)= 3x+2,等等,因此可以作以下总结:
结论已知连续函数y=f(x),x ∈[m,n],若经过其图像上三点的两条平行直线h1(x)=k0x+b1,h2(x)=k0x+b2满足关系式h1(x)≤f(x)≤h2(x),记则当且仅当时取最小.
证明设f(x)图像上满足条件的三个点的坐标为A(x1,y1),B(x2,y2),C(x3,y3),且m≤x1<x2<x3≤n,不妨设h1(x)经过A,C两点,h2(x)经过B点,那么

所以
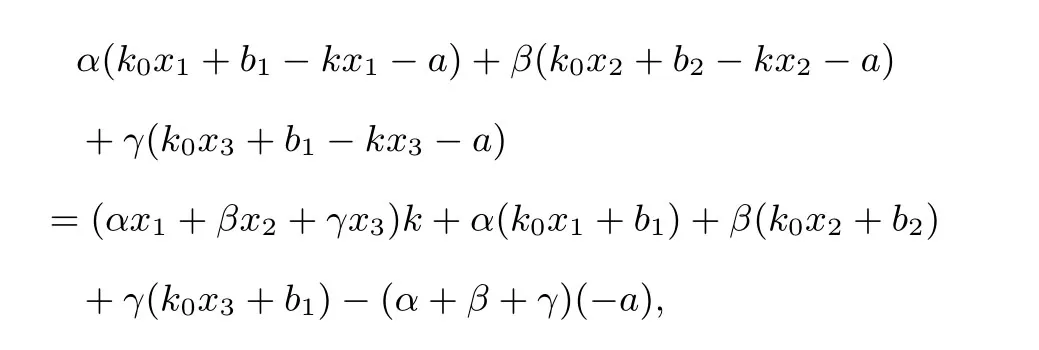
令α+β+γ=0,αx1+βx2+γx3=0,γ=-1,则那么α(k0x1+b1)+β(k0x2+从而即当且仅当k0x1+b1-kx1-a=k0x3+b1-kx3-a=-(k0x2+b2-kx2-a)时取“=”号,即k=k0并且时,
事实上,这类解法都是建立在切比雪夫逼近理论的基础上,由篇幅及高中教学要求所限,不再描述相关理论,有兴趣的读者可从文[2]中基于高观点的视角来透视这类题型的解法.

