2019年全国高中数学联赛一试A卷第10题的探究
广东省佛山市乐从中学
一、题目呈现
题目(2019年全国高中数学联赛一试(A卷)第10题)在平面直角坐标系xoy中,圆Ω与抛物线Γ:y2=4x恰有一个公共点,且圆Ω与x轴相切于抛物线Γ的焦点F,求圆Ω的半径.
二、解法探究
解法1(利用均值不等式)由题可知抛物线Γ的焦点为F(1,0),由对称性,不妨设圆Ω在x轴上方与x轴相切于F,设圆Ω的半径为r.故圆Ω的方程为


由均值不等式知

评注本解法是官方参考答案,其思路是基于:圆Ω与抛物线Γ:y2=4x恰有一个公共点,且圆Ω与x轴相切于抛物线Γ的焦点F⇔两曲线只有一个公共点,且r最小.所以只要求出r的最小值,并且取最小值时,y的值是唯一的.在求r的最小值时用到了四元均值不等式,这是其中一个思路难点.
解法2(利用导数)由解法1,可得令则所以f(y)在单调递减,在单调递增,于是当且仅当时,r取最小值
下同解法1.
评注解法2的思路与解法1是一致的,只是在求r的最小值时用导数法,技巧性较解法1低.
解法3(利用抛物线的切线方程)由题可知抛物线Γ的焦点为F(1,0),设圆Ω的半径为r,圆心为M.由对称性,不妨设圆Ω在x轴上方与x轴相切于F,故圆Ω的方程为(x-1)2+(y-r)2=r2.

图1
如图1所示,当圆Ω与抛物线Γ相切于点P时,圆Ω满足条件.设切点P(t20,2t0),则抛物线在点P处的切线方程为2t0y=2(x+t20),即t0y=x+t20,从而切线的斜率为又所以解得r=t30+t0.
又|MP|2=(t20-1)2+(2t0-r)2=r2,即t40+2t20+1-4rt0=0.所以t40+2t20+1-4t0(t30+t0)= 0,化简得解得所以,当时,所以圆Ω的半径为
解法4(利用公切线)由题可知抛物线Γ的焦点为F(1,0),设圆Ω的半径为r,圆心为M.由对称性,不妨设圆Ω在x轴上方与x轴相切于F,故圆Ω的方程为(x-1)2+(y-r)2=r2.
如图1所示,当圆Ω与抛物线Γ相切于点P时,圆Ω满足条件.设切点P(x0,y0),则圆Ω在点P处的切线方程为(x0-1)(x-1)+(y0-r)(y-r)=r2,化简得(x0-1)x+(y0-r)y=(x0-1)+ry0.同时抛物线在点P处的切线方程为y0y=2(x+x0),化简得2x-y0y=-2x0.
评注解法3与解法4的思路是:两个二次曲线若只有一个公共点,则两曲线必然相切.所以圆Ω与抛物线Γ:y2=4x恰有一个公共点⇔圆Ω与抛物线Γ相切,且两者在切点处的切线相同.两解法都要熟练掌握圆锥曲线的切线方程,不同之处是解法3只利用抛物线的切线方程;而解法4分别利用抛物线与圆的切线方程,且两切线是重合.所以在竞赛层面,要重视方法的积累和知识的储备,熟练掌握一些有用的结论,才有可能缩短思维的长度,提高效率,达到事半功倍的效果.
解法5(利用抛物线的光学性质)我们知道抛物线有如下的光学性质:
抛物线的光学性质从抛物线的焦点处发出的光线照射到抛物线上,经抛物线反射后,反射光线平行于抛物线的轴,且经过反射点的镜面所在的直线为抛物线的切线.
如图2所示,P是抛物线上任意一点,抛物线在点P处的切线为QT,则光线FP经过平面镜QT反射后的反射光线为射线PR.由反射定律,可知∠FPR的平分线PH垂直于切线QT(也称PH为切线QT的法线).
回到原题,如图3,设圆Ω的圆心为M,由对称性,不妨设圆Ω在x轴上方与x轴相切于F,且圆Ω与抛物线Γ相切于点P,在点P处的切线为QT,光线FP经过切线QT反射后的反射光线为射线PR,连接MP,MF,MR,FR.

图2

图3
由抛物线的光学性质可知∠FPM=∠RPM.又因为圆Ω在x轴上方与x轴相切于F,故由圆的性质可知∠PFM=∠RFM,所以M为ΔPFR的内心.另外M已是ΔPFR的外心,所以ΔPFR为正三角形.
设正ΔPFR的边长为a,则点P的坐标为由P在抛物线上可得解得在ΔPMF中,由正弦定理,得解得所以圆Ω的半径为
解法6(利用抛物线的光学性质及定义)如图4,设圆Ω的圆心为M,由对称性,不妨设圆Ω在x轴上方与x轴相切于F,圆Ω与抛物线Γ相切于点P,抛物线Γ的准线为l,作PG⊥l,垂足为G,GP与FM延长线交于点H,连接FP.
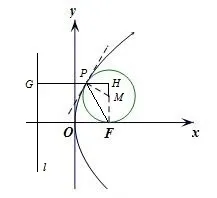
图4
因为圆Ω与抛物线Γ相切于点P,故PM是切线的法线,由抛物线的光学性质,可知PM平分∠HPF,从而∠HPM=∠MPF=∠MFP,易得∠FHP=900,故∠HPM=∠MPF=∠MFP=300,于是
评注光线的反射总是满足反射定律(入射角等于反射角),光线被曲线反射也不例外,抛物线的光学性质在解决与“切线”相关问题时会起到简捷作用,其要点往往是利用法线就是过反射点的曲线的切线的垂线.
以上的几种解法,从不同的角度出发思考问题,各显神通,这充分体现试题的不拘一格,一道试题往往考查多种能力、多种思想方法;试题思维方式、解答方法不是唯一的,给考生提供了较大的发挥空间.这样通过方法的选择、解题时间的长短,甄别出考生能力的差异,达到精确区分考生的目的.
另外,数学问题的解答,需要平时学习中的善于积累和勤奋钻研,只有通过量变达到质变,才能引起飞跃式的发展.熟练掌握一些有用的结论,考试时方能厚积薄发,达到“会当凌绝顶,一览众山小”的境界.
三、问题的提出
解答完本题后,思考:
问题1在原竞赛题中将抛物线一般化,即当Γ:y2=2px(p>0)时,则圆Ω的半径是多少?
问题2在原竞赛题中将抛物线改为椭圆或双曲线时,能否求得圆Ω的半径?
四、借题探究 结论推广
通过探究,可得如下结论:
结论1在平面直角坐标系xoy中,圆Ω与抛物线Γ:y2= 2px(p>0)恰有一个公共点,且√圆Ω与x轴相切于抛物线Γ的焦点F,则圆Ω的半径为
评析结论1的证明的可以参照原竞赛题的各种解法,显然,当p=2时正是原竞赛题的情形.
五、拓展探究 类比性质
我们知道,抛物线,椭圆与双曲线都是圆锥曲线,很多时侯三者之间有可类比的性质,这体现了圆锥曲线性质的内在统一的和谐美.那么素被称为“姊妹曲线”的椭圆与双曲线是不是也有类似于结论1的性质呢?经探究,得到如下结论:
结论2 在平面直角坐标系xoy中,圆Ω与椭圆恰有一个公共点,且圆Ω与x轴相切于椭圆Γ的焦点F,若c为Γ的半焦距,e为Γ的离心率,则圆Ω的半径为
为了更好地证明结论2,先给出一个引理:
引理若F是椭圆的焦点,点P是椭圆上的点,过点P的切线与焦点F对应的准线l交于点Q,PE⊥l,垂足为E,设椭圆的离心率为e,则
引理的证明如图5,不妨设F(c,0),对应的准线为l:则过点P的切线方程为

图5

图6
结论2的证明如图6,由椭圆的对称性,不妨设圆Ω在x轴上方与x轴相切于F,椭圆的焦点F(c,0),焦点F对应的准线为l:且圆Ω与椭圆Γ相切于点P,过点P的切线与准线l交于点Q,与x轴交于点D.
设圆Ω的圆心为M,连接MD,并与PF交于点H.作PE⊥l,垂足为E,设∠FPQ=α,∠EPQ=β,则易得
∠FDP=β.
由于圆Ω与椭圆Γ相切于点P,与x轴相切于Γ的焦点F,即DP,DF是圆Ω的两条切线,从而有DP=DF,且MP=MF,所以MD是PF垂直平分线.
又因为DP=DF,故有∠DPF=∠DFP=α.因为∠DFP+∠MFP=900,∠FMH+∠MFP=900,所以∠FMH=∠DFP=α,同理,易得∠FMH=∠PMH=∠DFP=∠DPF=α.
在RtΔPHD中,有∠DPH+∠PDH=由引理,得即cosα=ecosβ,而
所以cosα=e(1-2cos2α),即2ecos2α+cosα-e=0,解得从而sinα=
由椭圆的第二定义,得PF=ePE.另有PE=所以整理得将代入得所以在RtΔMFH中,得


结论3在平面直角坐标系xoy中,圆Ω与双曲线恰有一个公共点,且圆Ω与x轴相切于双曲线Γ的焦点F,若c为Γ的半焦距,e为Γ的离心率,则圆Ω的半径为
结论3的证明可参照结论2的证法,限于篇幅,不再给出证明过程.
评析在结论2的证明中,若以F为极点,x轴的正半轴为极轴,也可由椭圆的极坐标方程得到从结论2的证明可以看出,将原竞赛题的抛物线改为椭圆或双曲线,题目的运算量倍增,解答难度会高很多,这应是命题人使用抛物线的原由.结论1,2,3均已在数学软件GeoGebra中验证.
六、反思提升
从不同的思维角度分析同一道题目,得到不同的解题方法,一题多解的方式增加了题目涉及的知识广度,以一带多,减少了考查同样多的知识所需的题量.从数学知识的角度来看,通过解题发现知识的相互联系,体会知识之间的转化过程,从多角度地思考和发现问题,构建知识网络体系.这样,在学习基础知识、掌握基本技能的同时,能培养学生思维的广阔性、深刻性、灵活性以及创新性,能够使学生对学习的内容有一个整体的认识,并将知识融会贯通,举一反三,活跃思维,从而提炼出数学思想与方法,这正是数学教学的核心.
对题目的拓展、引申探究是一名数学教师必备的专业素养,平时要重视对典型问题的深入研究,探研规律,并适当拓展,充分挖掘题目的育人价值.高中数学新课程理念之一是倡导积极主动、勇于探索的学习方式,而学东西的最好方式是发现它,所以要鼓励学生通过合情推理对某些问题作大胆的猜想,并进行探索与证明,这样的探索在数学学习中起到重要作用.教师可根据学生实际,通过探究活动,让学生体验数学的发现和创造历程,引导他们勇于发现问题、提出问题、解决问题,进而让学生在分析、类比、猜想、证明过程中全面提高学生的综合能力,从而提升学生的数学核心素养.

