非等差等比数列常见模型问题的探究
南京外国语学校仙林分校
教材中建立等差数列和等比数列两种特殊的数列模型,教学过程中,通过归纳法、叠(累)加法、逐差法和迭代法等基础方法推导等差数列的通项公式,通过倒序相加法和首末求和法推导等差数列的前n项和公式,通过归纳法、叠(累)乘法和迭代法推导等比数列的通项公式,通过错位相减法、等比定理法推导等比数列的前n项和公式,根据学生分层教学情况,还可以介绍拆项法、乘法运算公式法和方程法推导等比数列的前n项和公式.
实际上遇到更多的是非等差等比数列,对于此类问题的常见模型做一些探究和方法总结,学习数列知识对进一步理解函数的概念和体会数学的应用价值具有重要的意义.
一、对于非等差等比数列,求其通项
例1(1)已知数列{an}中,a1=1,an=an-1+3n(n ∈N∗,n≥2),求通项公式an;
解法1由题意知:an-an-1=3n,an-1-an-2=3n-1,···,a2-a1=32,叠加得:当n≥2时,所以当n=1时,a1=1符合上式,所以

解法2当n≥2时,迭代得:
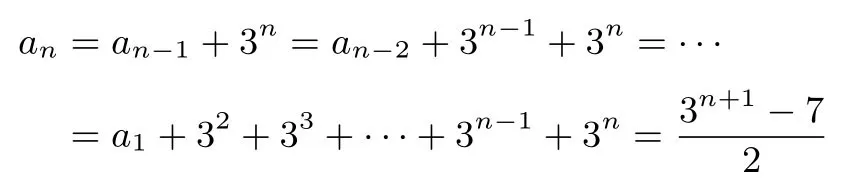
当n=1时,a1=1符合上式,所以
(2)已知数列{an}中,a1=1,nan=(n-1)an-1(n ∈N∗,n≥2),求通项公式an.
解法1由题意知:
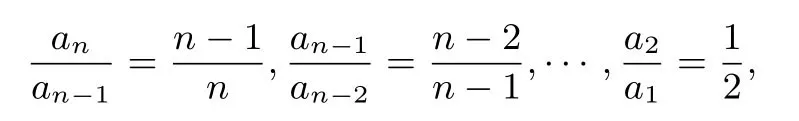
叠乘得:当n≥2时,

解法2由题意知:当n≥2时,迭代得:

当n=1时,a1=1符合上式,所以
解法3由题意知:nan=(n-1)an-1,则若将n·an视为整体,则当n≥2时,2·a2,3·a3,···,n·an,···构成一个常数列,所以n·an=2·a2=1,即当n=1时,a1=1符合上式,所以
方法小结对于例题中类等差等比数列通项公式的求解可以从多个角度求解,常规解法总结如下:
(1)形如an-an-1=f(n)(n ∈N∗,n≥2)的数列,应用叠加法:即当n≥2时,

注意:当n=1时不一定满足上述形式,所以需要检验;应用迭代法时,需要迭代后的式子方便求和化简.
例2(1)已知数列{an}中,a1+2a2+···+nan=n2(n+1),求通项公式an;
解当n≥2时,a1+2a2+···+nan=n2(n+1),a1+2a2+···+(n-1)an-1=(n-1)2n,两式相减得:nan=n2(n+1)-(n-1)2n=n(3n-1),所以an=3n-1,当n=1时,a1=2符合上式,所以an=3n-1.
(2)已知数列{an}中,a1a2···an=n2,求通项公式an.
解当n≥2时,a1a2···an=n2,a1a2···an-1=(n-1)2,两式相除得:所以an=当n=1时,a1=1不符合上式,所以an=
方法小结常规解法总结如下:
(1)形如a1+2a2+···+nan=f(n)的数列,a1=f(1),列出

(2)形如a1a2···an=f(n)的数列,a1=f(1),列出

注意:当n=1时不一定满足上述形式,所以需要检验.
二、对于非等差等比数列,求其前n项和
例3(1)求数列{1+2n-1}的前n项和Sn;
解分组求和:

解裂项相消:

(3)求数列{(-1)n(3n-2)}的前n项和Sn;
解法1错位相减法,
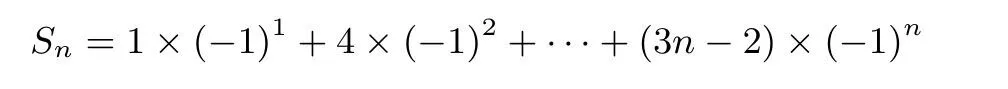
则

错位相减得:

解法2项数分奇偶数,并项相加法,
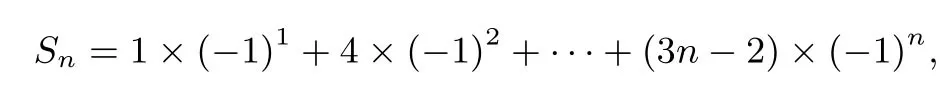
当n=2k(k ∈N∗),即时,
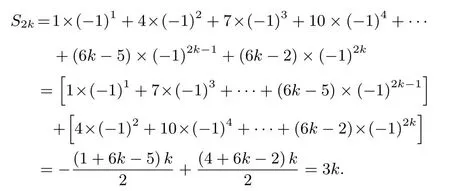
解错位相减法,

两式作差得:
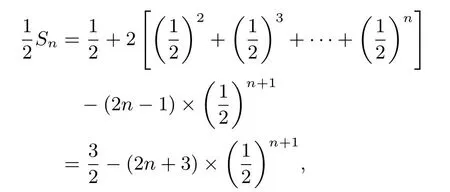
方法小结常规解法总结如下:
(1)形如an±bn(an,bn分别是等差数列和等比数列)的数列,应用分组求和法;
(3)正负交替出现的数列形式,应用错位相减法或者对项数n进行分类(奇偶性),应用并项相加法;
(4)形如anbn(an,bn分别是等差数列和等比数列)的数列,应用错位相减法.
三、根据数列的递推规律,求其通项
例4(1)已知数列{an}中,a1=1,1(n ∈N∗,n≥2),求通项an;
解由得:an-3 =又a1-3 =-2,所以an-30,则所以数列{an-3}是首项为-2,公比为的等比数列,于是an-3 =(-2)·则当n=1时,a1=1符合该式,所以
(2)已知数列{an}中,a1=1,an=2an-1+2n(n ∈N∗,n≥2),求通项an;
解由an=2an-1+2n(n ∈N∗,n≥2)得:又所以数列是首项为公差为1的等差数列,于是则当n=1时,a1=1符合该式,所以
(3)已知数列{an}中,a1=1,an=求通项an.
解由a1=1,an=得an0,所以(n ∈N∗,n≥2),即:所以数列是首项为1,公差为的等差数列,于是则当n=1时,a1=1符合该式,所以
方法小结常规解法总结如下:
(1)形如an=pan-1+q(n ∈N∗,n≥2,p1)的数列,化简为的形式,构造新数列,令即bn=pbn-1,原数列{an}转化成数列{bn}为等比数列,从而求得数列{an}的通项公式;
(2)形如an=pan-1+f(n)(n ∈N∗,n≥2)的数列,两边同除pn,得构造新数列,令即若刚好为常数,原数列{an}转化成数列{bn}为等差数列;若不是常数,但可以求和,原数列{an}转化为利用叠加法求数列{bn}的通项,从而求得数列{an}的通项公式;
注意:当n=1时不一定满足上述形式,所以需要检验;上面三种数列形式可以应用迭代法求通项,但需要迭代后的式子方便求和化简.
例5已知数列{an}中,a1=1,an+an+1=2n(n ∈N∗),求通项an.
解由题意知:a2=1.当n≥2时,an+an+1=2n,an-1+an=2(n-1),两式相减得:an+1-an-1=2,所以{an}的奇数项和偶数项都是公差为2的等差数列,所以
变式已知数列{an}中,a1=1,anan+1=2n(n ∈N∗),求通项an.
解析的奇数项和偶数项都是公比为2的等比数列,所以
方法小结常规解法总结如下:
(1)形如an+an+1=f(n)的数列,列出两式作差得an+1-an-1=f(n)-f(n-1),即找到隔项间的关系;
(2)形如anan+1=f(n)的数列,列出两式作商得即找到隔项间的关系;
上述两种形式的数列,在找到隔项间的数列关系后,可以转化为等差等比数列,非等差等比数列或类等差等比数列求通项的方法.
四、运用an与Sn之间的关系解决数列相关问题
例6已知数列{an}中,a1=1,Sn=n2an(n ∈N∗),求通项an.
解当n≥2时,an=Sn-Sn-1=n2an-(n-1)2an-1,化简得叠乘得
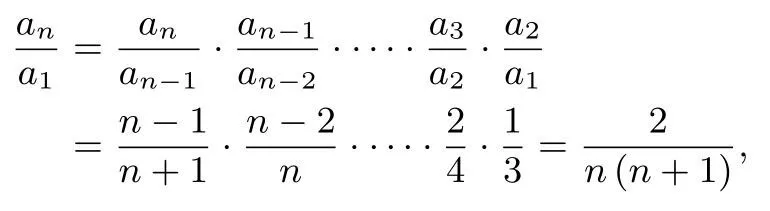
方法小结常规解法总结如下:
形如含an,Sn的关系式的数列,利用an=将递推关系转化为仅含有an的关系式(或仅含有Sn的关系式)解题.
注意:(1)当n=1时不一定满足得到的通项公式,所以需要检验;
(2)数列是从第1项起,还是从第2项或其他项起成等差等比数列;
(3)有时候需要进行多次迭代,有时候需要从数列{an}的子数列去探究{an}成等差等比的条件,仔细审题.
五、借助通项公式解决其他问题
理解通项公式对于解决数列问题的重要性,通过对通项的研究解决某些数列的单调性和最值问题,感受数列与函数的共性与差异,体会数学的整体性.
例7已知数列{an}的通项an=试问该数列{an}有没有最大项?若有,求出最大项的项数;若没有,说明理由.
解法1假设数列{an}有最大项为an,则即化简得解得
因为n ∈N∗,所以n=9或10,所以数列{an}有最大项,此时n=9或n=10.
解法2因为
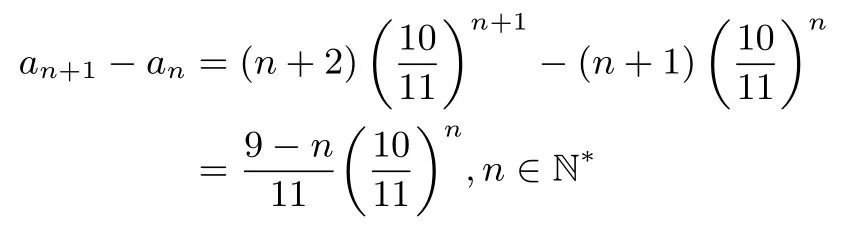
所以当n<9且n ∈N∗时,an+1-an>0,即an+1>an,此时数列{an}为递增数列;当n=9时,an+1-an=0,即a10=a9;当n>9且n ∈N∗时,an+1-an<0,即an+1<an,此时数列{an}为递减数列;即a1<a2<a3<···<a9=a10>a11>a12>···,所以数列{an}有最大项,此时n=9或n=10.
方法小结常规解法总结如下:
1.数列的单调性:
方法(1)转化为函数的单调性问题;
方法(2)利用an+1-an与0的关系或与1的关系(其中an>0)判断(证明)数列的单调性.
2.数列的最值:
方法(1)先判断数列的单调性,再求数列的最值;
方法(2)根据数列最值的定义,对任意的n ∈N∗,若第n项为数列的最大值,则若第n项为数列的最小值,则
六、解决数列问题过程中常见的思想
1.数列中的方程思想:等差数列两个基本量a1,d,等比数列两个基本量a1,q,等差数列和等比数列的两个基本问题an,Sn都可以用两个基本量来表示,利用基本量法解方程组;
2.数列中的化归和转化思想:处理数学问题常常可以将待解决的额问题转化为一类我们熟悉的问题来解决;
3.数列中的函数与数形结合思想:数列是一种特殊的函数,通项公式、前n项和公式都可以看成关于n的函数,各自有其特殊的函数特点,因此一些数列问题可以用函数的思想进行分析,加以解决;
4.数列中的数学建模思想:建立数列模型解决实际问题的过程中,可以培养学生发现、提出、分析和解决问题的能力,提高学生的基本数学素养.

