探寻“抽象”向“具象”转变的方法
——高中数学数形结合法的运用
江苏省启东中学 宋 波
“数”与“形”在数学课程中是对立又统一的关系,在数学教学中有效运用“数”与“形”之间的关系,有助于教师快速、高效地突破教学重难点,激发学生对数学学习的热情,积极探索数学“数”与“形”灵活转换的奥秘。纵观高中数学教学的现代化发展局势,数形结合已经成为广大数学教师的教学主线,并且通过数形结合法的渗透提高了学生的知识理解能力与知识应用能力,为学生指出了数学问题解决的捷径,对高中生的数学学习质量提升具有积极作用。
一、数形结合法在高中数学教学中应用的原则
数形结合主要是通过从数到形、从形到数或者利用向量法相互转换的一种数学学习方法,但是无论哪种转换方法在高中数学教学中的应用都需要遵循以下两点原则:
1.等价原则
数形结合中的等价原则是指几何性质与代数性质转化中的等价性,也就是说,无论是哪种转换方法,都必须保障数学问题中的“数”与“形”所反映出的数量关系一致。比如在数量关系转换为几何图形的时候,若是图形构造过于粗糙、精准性差,将会对学生数学问题的思考产生误导,从而导致结果出现偏差。由此可见,等价原则在数形结合教学方法在高中数学教学应用中起到关键作用。
2.双向性原则
数形结合方法在高中数学教学中的应用需要坚持双向性原则,让学生在几何问题的探究中学会借助直观的分析掌握代数抽象问题的解决方法,同时能够有效运用代数表达式克服几何直观运算问题中的诸多局限,在相互促进中提高学生的数形灵活转换与运用能力。
二、数形结合法在高中数学教学中的运用策略
1.在集合中的应用
集合作为苏教版高中数学第一章节内容出现,足见其重要性,通过数形结合在集合问题中的应用,可以帮助学生将抽象的集合问题以更加具象化的图形展示出来,让学生更加清晰地了解集合之间存在的隐蔽关系。如:学校组织学生参与社团活动,学生可以根据自己的喜好报多个社团,高一(4)班共30 人,其中15 人喜欢音乐、10 人喜欢围棋,还有8 人表示对这两项活动均不感兴趣,那么同时喜欢这两个社团的学生有多少人呢?此时教师可以引导学生利用绘制韦恩图的方式找出两个集合中的交集,设同时喜欢音乐与围棋的学生人数为x人,列式“(15-x)+x+(10-x)+8=30”,经过计算可得x=3,得出只喜欢音乐、围棋的人数则分别为12 人、7 人,让学生轻松解决集合问题。
2.在三角函数中的应用
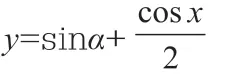
三、在解析几何中的应用
解析几何主要是研究曲线与方程问题的教学内容,“曲线”就是“形”,“方程”则是“数”,曲线与方程的教学内容为数形结合的应用提供了最佳的平台,最大化地体现了数形结合思想的数学价值,同时也是高中数学教师教学中普遍面临的难题。在曲线与方程问题的解决中运用数形结合方法需要以下几个步骤:第一步,建立直角坐标系;第二步,筛选出几何条件并将其转化为代数条件;第三步,通过代数的计算得出结果并将结果用几何的方式表现出来,以此提升高中生在解析几何中的学习成果。
四、在不等式中的应用
不等式在高中数学教学中占据着重要的地位,直接影响着学生解题能力的提升,因此教师应在不等式教学中渗透数形结合思想,让学生掌握数形结合在证明不等式、解含有参数不等式中的应用。如在“解关于x的不等式ax2-2 ≥2x-ax,其中a∈R”时,运用数形结合思想的基本思路为:(1)写出不等式代表的函数;(2)观察图像与图像之间是否存在交点;(3)解不等式问题得出答案。通过不等式转化为具象化的精准图像,为学生解决不等式问题提供了现行条件。
综上可知,数形结合在高中数学教学各个重点内容中的应用方法,教师应将数形结合思想渗透到课堂教学始终,让学生充分了解“数”与“形”转换的必要性,并且能够灵活运用数形结合方法,在数学问题解答中学会适当运用数形结合方式,以此帮助学生突破学习难点,提高高中生的数学解题能力,培养了高中生的数学思维,对于高中生今后学习与发展均具有深远的影响。

