数形结合思想在高中数学解题中的普遍应用

王亚茹

摘 要：数学是一门研究现实世界的空间形式与数量关系的科学，“代数”与“几何”的矛盾统一是引导数学发展的内在因素。在解题过程中运用该思想可以使解题更高效。作为贯穿初中、高中以及大学等数学学习过程中的一种重要的思想，教师在数学教学中突出该思想正是充分把握了数学的内在联系和灵魂所在的体现，有利于学生对概念以及定理的理解，加深学生的学习印象，从而建立起理论与实践只见那多维度的有效的联系。

关键词：高中数学;数形结合;解题

1 引言

数无形，少直观;形无数，难入微。数形结合思想的巧妙运用：使得一些代数问题得以通过图形的直观变得更具体;使得一些几何问题得以通过数量关系化繁为简。高中数学的教学内容和形式在新课程改革后产生了较大的转变。教学过程中，教师通过讲授基础知识点和讲解习题有意识地传授给学生数形结合思想，使得学生在学习过程中积极地促进该思想的主要价值的形成，同时积极鼓励学生在解题中运用该思想，分析问题，尽量避免出现逻辑混乱的情况。

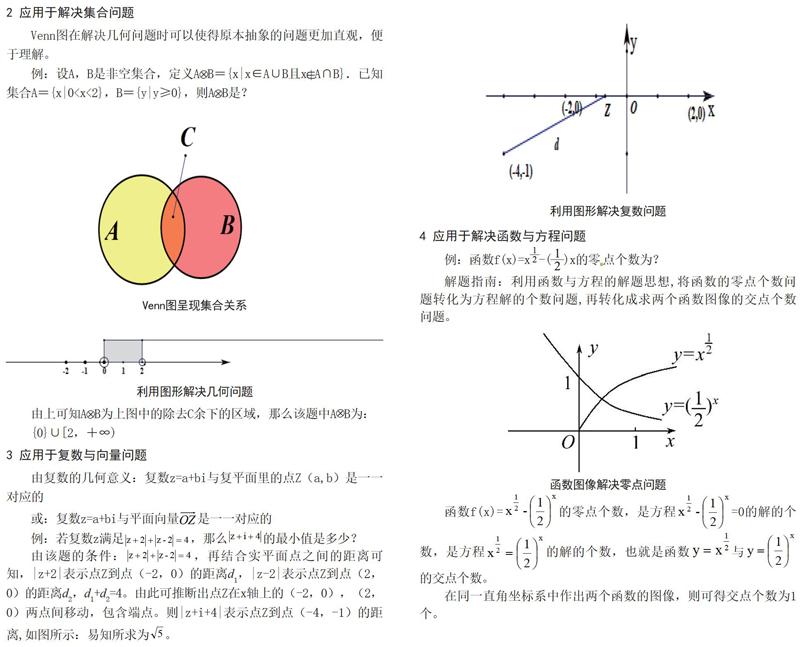
2 应用于解决集合问题

Venn图在解决几何问题时可以使得原本抽象的问题更加直观，便于理解。

3 应用于复数与向量问题

利用图形解决复数问题

4 应用于解决函数与方程问题

在同一直角坐标系中作出两个函数的图像，则可得交点个数为1个。

参考文献

[1]孙晓丽.数形结合思想在高中数学教学中的应用[J].当代教研论丛，2020（02）：64.

[2]廖雷，王涛.巧用数形结合思想提升中学生的解题能力[J].农家参谋，2018（17）：177.

[3]李花花.高中数学教学中运用数形结合提高解题能力的研究[D].天津师范大学，2008.

作者简介

王亞茹（1998-），女，汉，河南省柘城县，本科在读，学生，研究方向：数学与应用数学。