镍钛形状记忆合金循环变形行为的晶体塑性有限元模拟
陆辰钊,周 廷,于 超,康国政
(西南交通大学力学与工程学院,成都 610031)
引言
镍钛形状记忆合金(NiTi SMA)由于其固-固无扩散热弹性马氏体相变而表现出超弹性、形状记忆效应和高阻尼特性,在血管内支架、眼镜架、阻尼器、微机电系统中的执行器等领域得到了广泛应用[1-2]。由NiTi SMA制成的结构部件和器件经常承受着循环热-机械载荷作用[3]。因此,需要对NiTi SMA的热-机械循环变形行为进行研究,以合理准确地评估此类部件、器件的可靠性。
近年来,诸多学者对超弹性NiTi SMA的循环变形行为进行了相关实验和理论研究。实验方面,Miyazaki等[4]的研究结果表明,NiTi SMA的超弹性在循环变形过程中会发生退化,主要体现在相变临界应力和耗散能降低、残余应变累积、相变硬化模量增加这几个方面,且这些现象在一定循环周次后趋于饱和。进一步的实验研究[5-11]揭示了这种超弹性退化与加载峰值、加载速率、加载路径和环境温度之间的相关性。此外,为了明确循环变形行为的微观机理,Delville等[12]、Benafan等[13-14]、Hamilton等[15]、Norfleet等[16]、Hua等[17]、Xiao等[18]、Pfetzing-Micklich等[19]、Brinson等[20]通过透射电镜等微观观测手段,解释了残余应变累积的物理机制,即奥氏体相中的位错滑移、残余马氏体相的循环累积以及位错-相变交互作用。
理论模型方面,根据空间尺度的不同,描述形状记忆合金热-力变形行为的本构模型大致可以分为宏观唯象模型和晶体塑性模型两大类[21]。宏观唯象模型通过引入宏观内变量及相关演化方程来描述实验研究揭示的循环变形行为演化特征,此类模型不关注材料微结构演化,具有计算量小,适用于工程应用的优点。晶体塑性模型则是建立在单晶尺度上,通过确定的晶体取向关系来度量非弹性应变,可以方便地将不同的非弹性变形机制引入到模型中[22],再通过尺度过渡准则或有限元方法将单晶模型拓展到多晶情形。与宏观唯象模型相比,晶体塑性模型充分地考虑了材料微结构形态及其演化,具备坚实的物理背景[22],并且能够为材料微观结构设计与优化提供理论指导。
然而,上述晶体塑性本构模型仅仅考虑了马氏体相变这一种非弹性变形机制,无法描述镍钛形状记忆合金在循环变形过程中出现的超弹性退化现象。最近,Yu等[23]通过同时考虑马氏体相变、相变诱发塑性以及二者交互作用,建立了基于晶体塑性的循环本构模型。然而,该模型采用了显示过渡准则完成从单晶到多晶的过渡。该过渡准则属于平均场理论的范畴,即无法给出合金循环变形过程中应力、应变以及内变量场在晶粒内部的非均匀分布。因此,为了合理度量多晶体中不同晶粒之间的交互作用并反映非均匀变形特性,本文首先基于Yu等[22]建立的单晶循环本构模型,通过编写通用有限元软件Abaqus中的用户材料子程序(VUMAT)来完成对该模型的有限元移植。然后,建立多晶代表性体积单元,引入<111>型初始织构。最后,通过模型计算讨论了外部加载条件(应力水平)和内部微结构特征(织构强度)对镍钛形状记忆合金超弹性循环退化的影响。
1 本构模型及数值算法
1.1 本构模型
本节首先对Yu等[23]提出的形状记忆合金晶体塑性循环本构模型进行简要介绍。该模型建立在单晶尺度上,考虑了24个马氏体变体和奥氏体-马氏体界面错滑移系。进一步建立了材料点的Helmholtz自由能,并在热力学框架下,通过耗散能不等式推导出相变和位错滑移的热力学驱动力,进而提出了内变量(包括马氏体体积分数和塑性滑移量)演化方程,具体细节可参见原始文献[23]。
1.1.1 应变分解
基于小变形假设,将总应变ε分解为弹性应变εe、应力诱发相变应变εtr和相变诱发塑性应变εtp:
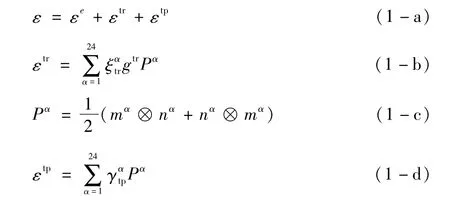
1.1.2 相变驱动力及内变量演化

其中,T为温度,为第α个马氏体变体的平衡温度,Btr为相变内应力张量,是第α个变体的相变阻力,可表示为:

其中d、c1是材料参数,是马氏体相变相关的第 α个马氏体变体导致的内应力的大小,是第α个马氏体变体的相变模量。是位错密度为零状态下的初始相变模量,Htr-p反映位错滑移对相变模量的影响。

其中,Yα是一个控制马氏体相变滞回环宽度的正变量,Y0是位错密度为零状态下的初始量,反映位错滑移对滞回环宽度的影响,m表征了马氏体相变的粘性,由于镍钛形状记忆合金中马氏体相变粘性很弱,因此,这里m值取为50。
为反映位错滑移对相变模量和滞回环宽度的影响,Htr-p和的演化率可表示为:

其中,c2和c3是材料参数。
1.1.3 塑性驱动力及内变量演化
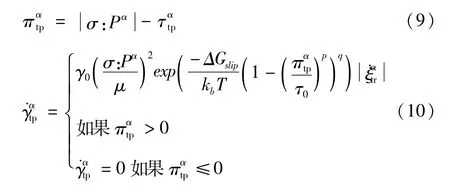

其中,ρα是第α个滑移系的位错密度,k1和k2是材料参数,k1项反映了位错的生成,项反映了位错的湮灭,b是镍钛形状记忆合金的Burgers矢量的大小。
1.2 数值算法
本文通过编写用户材料子程序VUMAT将上述本构关系移植到有限元软件Abaqus中。假设第n步的应力σn、应变 εn以 及 内 变 量 如 (Btr)n、(、((Yα)n、(、(ξtr)n、、(ρα)n均为已知。在第n+1步,给出应变增量 (Δε)n+1和时间增量 (Δt)n+1,可得应变张量εn+1=εn+(Δε)n+1,需要计算的未知量为(Btr)n+1、 (、 (、 (Yα)n+1、 ((ξtr)n+1、(、(ρα)n+1、σn+1。在第 n+1个加载步中,使用以下的显式数值算法:
(1)在第n+1步开始时,VUMAT子程序从用户定义变量中读取需要的变量。从Abaqus主程序得到应力、应变增量、时间增量和温度。
(2)计算相变驱动力和马氏体相变体积分数增量。

(3)为了使马氏体体积分数保持在合理范围,防止算法发散,应该对马氏体体积分数增量做一些微调,随后更新马氏体体积分数。

(4)计算相变诱发塑性驱动力和塑性滑移量。
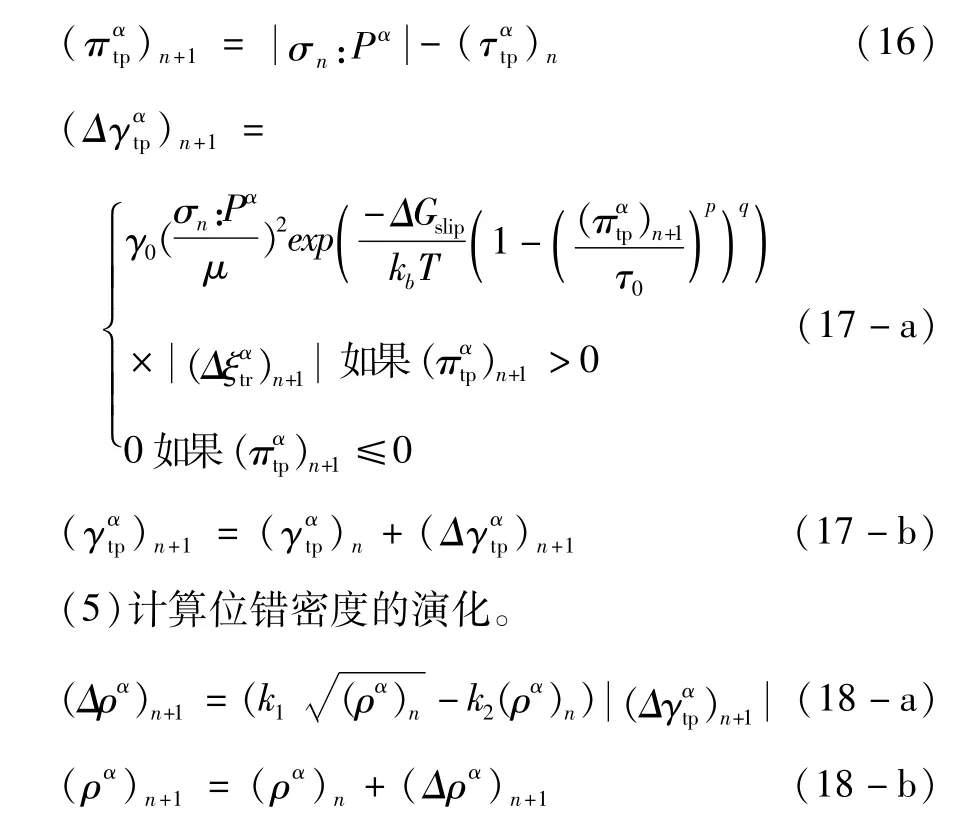
(6)根据位错密度更新滑动阻力和相变内应力。

(7)更新相变模量和相变阻力。

(8)更新滞回环控制参数。


(9)更新相变应变、相变诱发塑性应变及弹性应变。

(11)将更新的变量写入子程序的自定义变量中,将数据返回给Abaqus主程序。
1.3 材料参数
参考Yu等[23]的工作,计算中使用的材料参数见表1。

表1 模型参数
2 多晶代表性体积单元有限元模型
计算模型如图1所示,使用一个5×5×5的立方体来构建一个多晶代表性体积单元。模型采用8节点立方体单元C3D8,模型中每一个单元代表一个奥氏体相晶粒,模型共包含125个晶粒。通过在VUMAT程序中使用旋转矩阵对24个马氏体变体的晶体学参数矢量进行旋转,以得到整体坐标系下每个晶粒的相变切边方向、惯习面法线方向、位错滑移方向和位错滑移面法线方向。对于常用的NiTi形状记忆合金板材、管材、丝材和棒材,其加工成型工艺通常会导致试样具有强<111>型初始织构。因此,本文将在有限元模型中考虑这一种类型的织构,采用晶粒取向与<111>方向的摆动角度大小来描述织构强度,角度越小代表织构越强,即0°角时退化到单晶、90°角时退化到无织构随机取向多晶。本文计算中,规定底面(y=0)的位移uy=0,并规定顶面(y=1)处位移uy=˙Eyt,其中,˙Ey为应变率。

图1 立方体模型网格划分
3 模拟结果与讨论
本节将利用Yu等[23]建立的晶体塑性循环本构模型和本文建立的多晶代表性体积单元模型对NiTi形状记忆合金在循环变形过程中出现的超弹性退化现象进行模拟,并讨论外部加载条件(应力水平)和内部微结构特征(织构强度)对循环变形行为的影响。
3.1 加载水平对循环变形的影响
首先固定织构强度(15°摆动角),讨论加载水平对循环变形行为的影响。峰值应变分别取4%,7%和10%,加载10圈。第1圈和第10圈应力-应变曲线以及残余应变随循环演化曲线分别如图2和图3所示。

图2 不同加载水平下应力应变曲线图

图3 不同加载水平下残余应变的循环演化曲线
从图2和图3中可以看出,模型能够很好的捕捉到NiTi形状记忆合金在循环变形中出现的超弹性退化现象,即残余应变累积、相变临界应力降低、滞回环面积减小和相变模量升高。同时,随着加载水平的增加,相同循环圈数下的残余应变的累积与相变开始应力的下降更加明显。这是由于应变幅值越大,发生相变的马氏体体积分数越高,使得相变诱发塑性量越多,位错密度也就越大。且随着循环的进行,高加载峰值下较高的位错密度对超弹性退化的影响越显著,从而导致残余应变的累积和相变临界应力的降低越明显。也就是说,超弹性循环退化行为随着加载水平的提升而加剧。模拟结果与现有的实验结论相吻合[8]。
3.2 织构强度对循环变形的影响
接下来固定峰值应力(800 MPa),讨论织构强度对循环变形的影响。摆动角分别取为 5°、10°、15°、20°和25°,第1圈和第10圈应力-应变曲线以及残余应变随循环演化曲线分别如图4和图5所示。

图4 不同织构强度应力应变曲线图
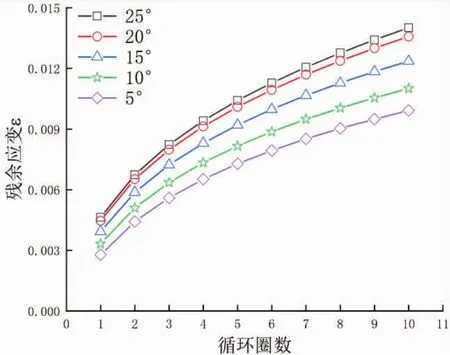
图5 不同织构强度残余应变的循环演化曲线
图4和图5的结果表明,在加载的第1圈,织构强度越强,相变模量越低,导致相变束应力和逆相变开始应力越低;在加载的第10圈,织构强度越强,累积的塑性应变越少,相变开始应力随循环减少的幅度也就越少。也就是说,超弹性循环退化行为随着织构强度的提升而减弱。
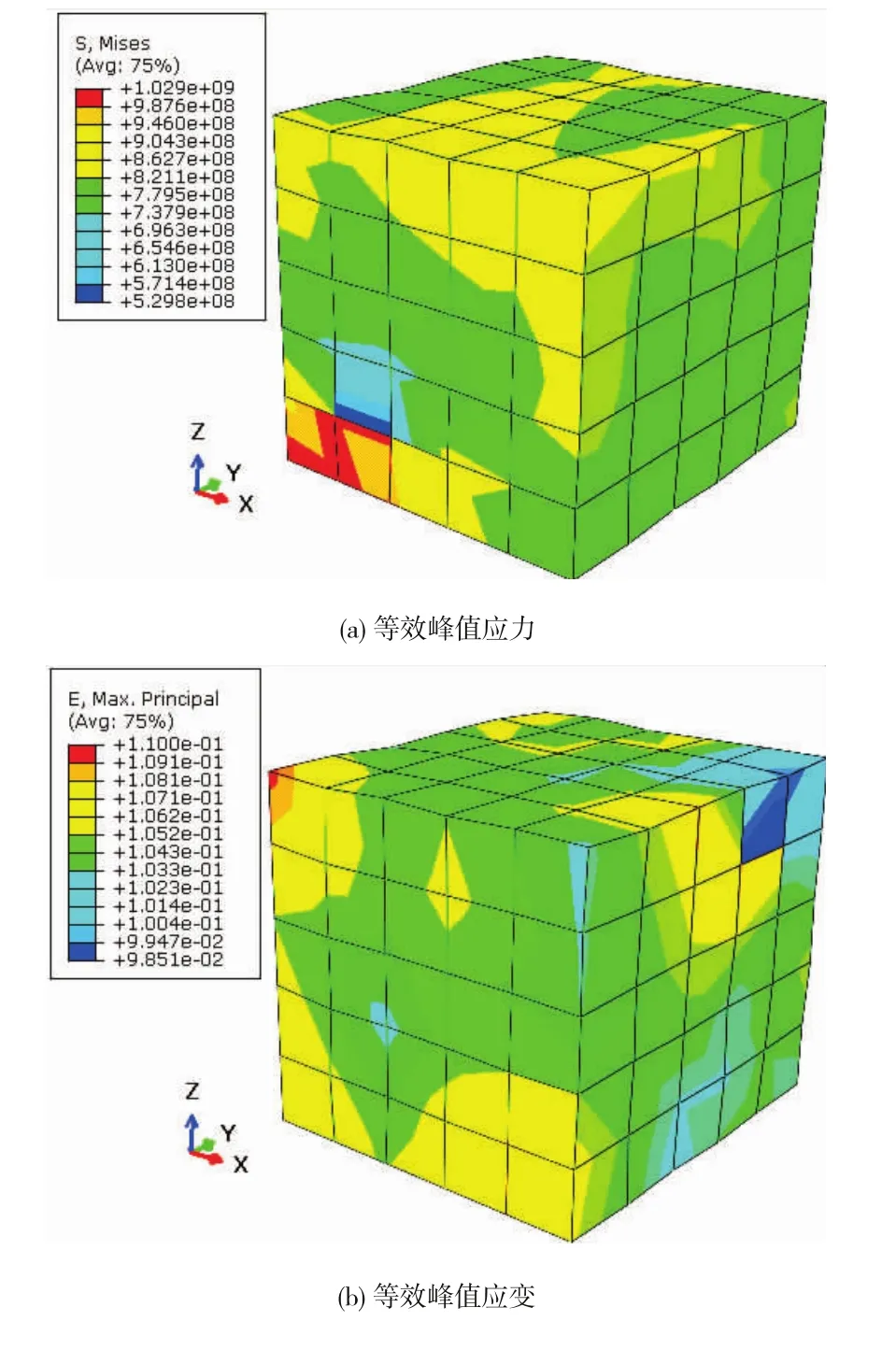
图6 摆动角为15度模型循环变形第10圈应变分布云图
图6给出了多晶代表性体积单元在循环变形第10圈变形最大点的等效应力(Mises应力)和等效应变分布云图。可以看到,由于晶粒取向的不同,各个晶粒存在着较强的交互作用,这使得多晶代表性体积单元在循环变形过程中应力-应变场出现明显的非均匀性。

图7 摆动角为15度模型循环变形10圈后分布云图
图7给出了多晶代表性体积单元在循环变形10圈后的等效残余应力(Mises应力)和残余应变分布云图。图中可见,由于塑性变形的发生,多晶代表性体积单元在循环变形后存在残余应变,并且由于残余应变的非均匀性,诱发了较高的残余应力。
4 结论
本文基于Yu等[23]建立的考虑马氏体相变和相变诱发塑性的镍钛合金晶体塑性循环本构模型,通过对本构方程进行数值离散化编写了Abaqus用户材料子程序(VUMAT)。进一步建立了有多晶代表性体积单元的有限元模型,考虑合金在成型过程中最常见的<111>织构,讨论了加载水平和织构强度对循环应力-应变响应的影响。可以得到以下几点结论:
(1)循环应力-应变响应显著依赖于应变加载水平,超弹性退化现象随着加载水平的提高而更加显著;
(2)循环应力-应变响应显著依赖于织构强度,超弹性退化现象随着织构强度的提高而减弱;
(3)由于多晶体中各个晶粒晶向的差异性,多晶代表性体积单元应力-应变场呈现非均匀性。同时,由于塑性变形的逐渐累积和其非均匀性,合金在循环变形后存在较高的残余应力。

