氯氧镁水泥混凝土中涂层钢筋的耐久性退化研究

王鹏辉, 乔宏霞,2, 冯 琼, 曹 辉, 温少勇

(1.兰州理工大学 甘肃省土木工程防灾减灾重点实验室， 甘肃 兰州 730050；2.中国科学院 青海盐湖研究所， 青海 西宁 810083)

中国“一带一路”中线所经大部分地区为盐渍土盐湖地区[1-2]，因土壤中碳酸盐、重碳酸盐、硫酸盐、氯盐等有害离子含量较高而使得普通钢筋混凝土构建筑物未达设计规定的年限即遭破坏[3-4].氯氧镁水泥作为MgO-MgCl2-H2O体系组成的镁质胶凝材料[5]，不经改性就具有很强的抗盐卤性能，使其在盐渍土地区的应用成为可能.因此氯氧镁水泥混凝土中涂层钢筋的耐腐蚀性就成为了该种混凝土耐久性的决定性因素.海洋工程中常利用涂层防护技术对金属进行保护，经研究发现，利用涂层对钢筋进行保护是一种高效有用的方法[6-9]，因此通过涂层对氯氧镁水泥混凝土中的钢筋进行保护是可行的.通过电化学试验对钢筋混凝土中钢筋锈蚀状态进行分析的方法已较为成熟.姬永生等[10]、许晨[11]、乔宏霞等[12-13]、史美伦等[14]采用电化学试验对混凝土(镁水泥混凝土)中钢筋的锈蚀从极化曲线和交流阻抗方面进行了深入分析.因此以电化学试验中钢筋锈蚀的相关参数作为钢筋耐久性退化因素是合理可靠的.Weibull函数作为一种连续分布函数，可以描述失效数据的分布规律，在可靠度设计和寿命数据分析中有一定的应用.赵威等[15]利用Weibull函数对短时间内白光有机发光二极管(OLED)的寿命进行了预测.张建平等[16]利用Weibull函数对红外发光二极管(LED)的加速寿命进行了预测.宋辉[17]利用Weibull函数描述易腐蚀物品的变质特性，建立起易腐蚀物品的最优订货策略.宋玉普等[18]把混凝土结构冻融损伤近似看作由不同正负峰值温度差顺序作用所产生，在三参数Weibull函数的基础上推导出冻融循环作用后混凝土剩余寿命计算公式.Martínez-Antúnez等[19]对墨西哥杜兰戈温带森林中环境变量与树种丰富度之间的关系进行研究，得出15个物种服从三参数Weibull函数分布，6个物种服从二参数Weibull函数分布的结论.黄昆林[20]根据Weibull-Markov模型，提出了较传统Monte-Carlo法计算更为简单、精度更高的配电系统中断成本评估方法.Fetisova等[21]在Weibull函数基础上提出的研究方法，可解决在不同风轮轴高度和不同风力涡轮机特征下，当缺乏关于风速可重复性的垂直分布信息时，为设计供电系统提供有效设备选择的问题.Bonadonna等[22]引进了等厚板面积与平方根之间的Weibull函数，很好地描述了等值面积平方根的最大石块的尺寸衰减，以及羽流高度如何与相应的Weibull参数强相关.然而将Weibull函数应用于氯氧镁水泥钢筋混凝土中的钢筋失效时间预测还未见相关报道.

为此，本文采用电化学工作站实测的表征钢筋锈蚀的腐蚀电流密度作为钢筋锈蚀寿命的退化指标，通过最小二乘法(LSE法)、矩估计法(ME法)、最大似然法(MLE法)对Weibull分布参数进行估计，最终得到氯氧镁水泥钢筋混凝土中涂层钢筋锈蚀寿命的可靠度函数和概率密度函数，从而对氯氧镁水泥钢筋混凝土中的钢筋失效时间进行预测.

1 试验

1.1 原材料

轻烧氧化镁(MgO)、氯化镁(MgCl2)：青海省格尔木市察尔汗盐湖氯化镁厂生产.砂子：兰州水阜河砂，中砂，级配良好.石子：兰州华陇商砼公司提供的碎石，属于连续级配，性能指标合格.粉煤灰：Ⅰ级粉煤灰(用于改善混凝土耐久性)，兰州某钢厂生产.耐水剂：磷酸，天津市百世化工有限公司生产， H3PO4质量分数不小于85.0%，色度不大于25黑曾.减水剂：KD萘系高效减水剂JM-PCA(I)，江苏苏博特新材料有限公司生产，其基本物理性能见表1，其中的抗压强度比是指掺减水剂之后与之前的混凝土抗压强度之比值.水：自来水，符合JGJ 63—2006《混凝土拌合用水标准》要求.钢筋：HPB300钢筋，屈服强度fy= 300N/mm2.钢筋涂层：日本久美(GEOMET)，其中含有超细的锌铝鳞片，锌的质量分数为90%，宁波计式金属表面处理有限公司提供.氯氧镁水泥混凝土的配合比如表2所示，砂浆坍落度为120mm.

表1 JM-PCA(I)减水剂各项物理指标

Table 1 Physical indicators of water reducing agent(JM-PCA(I))

Density/(g·mL-1)pHvaluew(alkali)/%Water reductionrate(by mass)/%Bleedingrate/%Compressivestrength ratio of concrete/%3d7d28dRecommendeddosage(by mass)/%0.00038.08≤3.883401681491390.75-1.50

表2 氯氧镁水泥混凝土配合比Table 2 Mix proportion of magnesium oxychloride cement concrete kg/m3

1.2 试验方案

光圆钢筋直径8mm，长度105mm.钢筋经酸洗、碱洗、去污除油，经自然晾干后涂刷平均厚度约80μm的GEOMET涂层.按照表2配合比制备尺寸为100mm×100mm×100mm的氯氧镁水泥混凝土试块，然后将涂层钢筋置于其中，混凝土保护层厚度为25mm.最后将制备好的钢筋混凝土试块置于氯离子浓度为1.5mol/L的氯化镁溶液中，溶液高度达到试块高度的2/3处.利用科斯特CS350电化学工作站，以试块中的涂层钢筋为工作电极，其电极面积为25.12cm2；不锈钢薄板为辅助电极，其电极面积为30.00cm2，大于工作电极面积；饱和KCl电极为参比电极，于室内环境下进行溶液浸泡加速锈蚀试验，从4d、90d，此后每隔90d测试1次试块中涂层钢筋的极化曲线参数.电化学试验三电极系统电解池测试示意图如图1所示；钢筋腐蚀电流密度icoor与钢筋锈蚀程度的对应关系如表3所示.另外，经过990d溶液浸泡加速锈蚀试验后，破坏钢筋混凝土试块，刮掉其中钢筋上的涂层，采用JSM—6700F冷场发射扫描电子显微镜(SEM)和日本理学公司(Rigaku)生产的D/max-2400粉末X射线衍射仪(XRD)对钢筋进行微观分析.

图1 三电极系统电解池测试示意图Fig.1 Three-electrode system electrolytic cell test schematic

表3 钢筋腐蚀电流密度与锈蚀程度之间的对应关系Table 3 Corresponding relationship of corrosion current density and corrosive degree of steel bars

2 试验结果与分析

2.1 极化曲线分析

图2为涂层钢筋在氯化镁溶液浸泡加速锈蚀试验中得到的极化曲线.

由图2可见：4d时的涂层钢筋腐蚀电位为-0.670V左右；90d前，腐蚀电位出现负向移动， 90d 时腐蚀电位约为-0.875V.电位出现负向移动表明腐蚀容易发生.原因是涂层中含有大量的锌铝鳞片，Zn的自然腐蚀电位为-0.762V，Fe的自然腐蚀电位为-0.440V，Zn作为牺牲阳极为基体提供阴极保护，因此开始阶段涂层钢筋的腐蚀电位发生负向移动.90～900d期间，涂层钢筋的腐蚀电位不断出现正向移动，到900d时腐蚀电位约为 -0.570V.原因是涂层中的锌铝鳞片不断发生锈蚀，生成碱式碳酸锌(Zn5(OH)6(CO3)2)和碱式氯化铝(Al5Cl3(OH)12·4H2O)，从而堵塞了涂层孔道，抑制了锈蚀的进一步发生.其化学反应方程式为：

(1)

(2)

图2 涂层钢筋的极化曲线图Fig.2 Polarization curves of coated steel bar

900～990d期间，腐蚀电位又从-0.570V左右负向移动到-0.600V左右，原因是氯离子不断地向涂层内部渗透，致使涂层孔道增加，涂层电阻减小、电容增大.由CS350电化学工作站内部软件拟合计算得出的涂层钢筋腐蚀电流密度如表4所示.由表4结合表3可知，在990d时涂层钢筋依然处于轻微锈蚀状态.

表4 涂层钢筋的腐蚀电流密度Table 4 Corrosion current density of coated steel bar μA/cm2

2.2 微观分析

经过990d溶液浸泡加速锈蚀试验后，为判断涂层对钢筋的保护效果，刮除钢筋外部的涂层，然后对裸露的钢筋进行微观分析，其SEM照片如图3所示.对图3中的白圈部位进行XRD分析和EDS分析，结果如图4、表5所示.

图3 涂层钢筋的SEM照片Fig.3 SEM photo of steel bar

图4 钢筋(图3白圈部位)的XRD图谱Fig.4 XRD pattern of steel bar(white circle in Fig.3)

由图3可见：钢筋表面存在白色疏松状球簇晶体并伴有少量灰色物质，这可能是涂层中的Zn鳞片、Al鳞片代替涂层发生了牺牲阳极反应所生成的 Zn5(OH)6(CO3)2、Al5Cl3(OH)12·4H2O.由图4并结合表5可知，钢筋主要元素仍为Fe，O的含量较少，表明钢筋仅发生了轻微锈蚀，且锈蚀的主要发生部位在涂层钢筋表面，即涂层很好地保护了钢筋.

表5 钢筋(图3白圈部位)的EDS扫描结果Table 5 EDS scanning results of steel bar(white circle inFig.3)

3 基于Weibull函数建模

Weibull函数由Weibull于1939年首次提出，由于其能以小样本数据得出较精确的预测而被广泛应用于寿命问题的研究.Weibull函数有二参数和三参数2种情况.本文将基于二参数Weibull函数，对氯氧镁水泥混凝土中的涂层钢筋锈蚀状况进行耐久性建模.耐久性建模步骤如下：首先检验耐久性退化指标(腐蚀电流密度)是否服从Weibull函数分布；其次分别采用最小二乘法、矩估计法、最大似然法对未知参数进行估计；最后利用Matlab软件作出可靠度函数R(t)曲线，进行耐久性评价.

3.1 Weibull函数理论基础

二参数Weibull函数表达式如下：

(3)

式中：t为腐蚀时间；β为大于0的形状参数；η为大于0的尺度参数，记作T～Wei(η,β).

其概率密度函数为：

(4)

其可靠度函数为：

(5)

其失效率函数为：

(6)

3.2 Weibull函数分布检验

采用P-P(Expected cum prob-Observed cum prob)图对涂层钢筋的腐蚀电流密度进行Weibull函数分布检验，结果如图5所示.如果数据点在P-P图中沿对角线分布、在去趋势P-P图中呈散点状分布，则表明该数据服从所检验的函数分布[23].

由图5可见，涂层钢筋的腐蚀电流密度大致服从Weibull函数分布.为了进一步确定其是否满足Weibull函数分布，采用假设检验对其进行分布检验，所得到的概率图如图6所示，其中置信水平α=0.05.由图6可以看出，各数据点均在95%的置信区间内，通过计算得出接受假设函数的概率P=0.25>0.05，表明涂层钢筋腐蚀电流密度确实服从Weibull函数分布.

图5 涂层钢筋腐蚀电流密度的Weibull函数分布检验图Fig.5 Weibull function distribution test chart of corrosion current density of coated steel bar

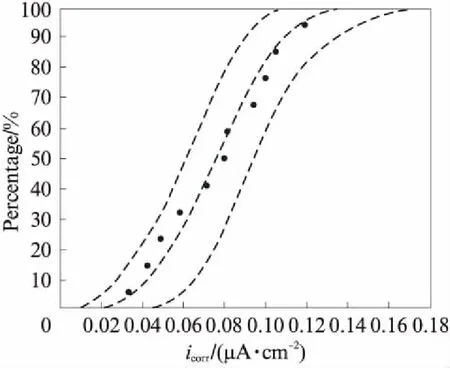
图6 涂层钢筋腐蚀电流密度概率图Fig.6 Probability diagram of coated steel bar corrosion current density

3.3 Weibull函数的参数估计

基于Weibull函数建立的涂层钢筋耐久性模型在可靠性工作中表现是否优秀与参数估计值的精确度相关，特别是在小样本情况下进行的可靠性研究.因此，为提高耐久性模型在工作中的可靠性，采用多种参数估计方法对未知参数进行估计，旨在获得较为准确的参数估计值.

3.3.1最小二乘法(LSE法)

将式(5)两边取对数，化简整理得可靠度函数为：

ln[-lnR(t)]=βlnt-βlnη

(7)

令y=ln[-lnR(t)],x=lnt.则式(7)可化简为：

y=ax+b

(8)

由于某一时间点的腐蚀电流密度是恒定不变的，因此可定义某一时间点的钢筋相对锈蚀程度D1为：

(9)

式中：icoor为某一时间点的腐蚀电流密度，见表6；imc为腐蚀电流密度的破坏阀值，取为1μA/cm2.

钢筋的锈蚀直接影响其力学性能的优劣，因此为保证结构的安全性，此处取钢筋锈蚀程度达到60%时为其破坏阀值.令ω1为相对锈蚀评价参数，其计算式为：

(10)

D1和ω1的计算结果如表6所示.

表6 钢筋相对锈蚀程度和相对锈蚀评价参数Table 6 Relative corrosion degrees and relative corrosion evaluationparameters of steel bar

令y=ln(-lnω1),x=lnt，将ω1的计算结果代入得y、x，其计算结果如表7所示.利用最小二乘法(LSE法)对式(8)进行求解[24-25]，可得出β= 0.8249，η=3283.7.

表7 系数计算表Table 7 Coefficient calculation table

3.3.2矩估计法(ME法)

设X～Wei(η,β)，X1,X2,…，Xn为其完全样本，则其矩估计为[26]：

(11)

(12)

由Weibull函数的性质得出：

(13)

(14)

则β与η的估计值为：

(15)

(16)

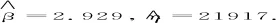
3.3.3最大似然法(MLE法)

设X～Wei(η,β)，X1,X2,…，Xn为其总体的独立样本，则其最大似然函数为：

(17)

对式(17)取对数得：

(18)

分别对式(18)中的η和β求偏导，并令其等于0，得：

(19)

(20)

由此可得：

(21)

(22)

式(22)为超越方程，求解此方程需要用数值解法，例如二分法、Newton迭代法等，本文采用二分法对其进行求解[27].设：

(23)

并由最小二乘法和矩估计法得出β∈[0.8249,2.9290]或者更大的区间，因此取β∈[0.9,3.0]进行迭代，当精度达到小数点后4位数时停止迭代.其计算结果如表8所示.由表8可见，到第15次迭代时，已能精确到小数点后4位数，最终求得β=1.79835，η=12600.35.

4 可靠性评估

将最小二乘法、矩估计法、最大似然法的参数估计值分别代入式(4)、(5)，所得到的涂层钢筋概率密度函数f(t)曲线和可靠度函数R(t)曲线如 图7、8所示.

由图8可见，采用最小二乘法、矩估计法和最大似然法得到的涂层钢筋可靠度曲线在整个退化过程中存在较大差异，虽然其最终失效时间都在 38000d(104.1a)左右，但是对于可靠度为0.4时所对应的失效时间R(t0.4) 来说，这3种估计方法还是存在较大差异的，分别为2960d(8.1a)、12000d (32.9a)、21210d(58.1a).因此参数估计方法的不同对涂层钢筋耐久性退化可靠度计算有很大影响.将3种估计方法得到的可靠度与表6中相对锈蚀评价参数ω1对比后发现，最小二乘法(LSE法)的估计值与ω1偏差最小，只有3.5%左右.因此Weibull函数中通过LSE法所得到的涂层钢筋可靠度曲线能够最直观地反映其退化过程.

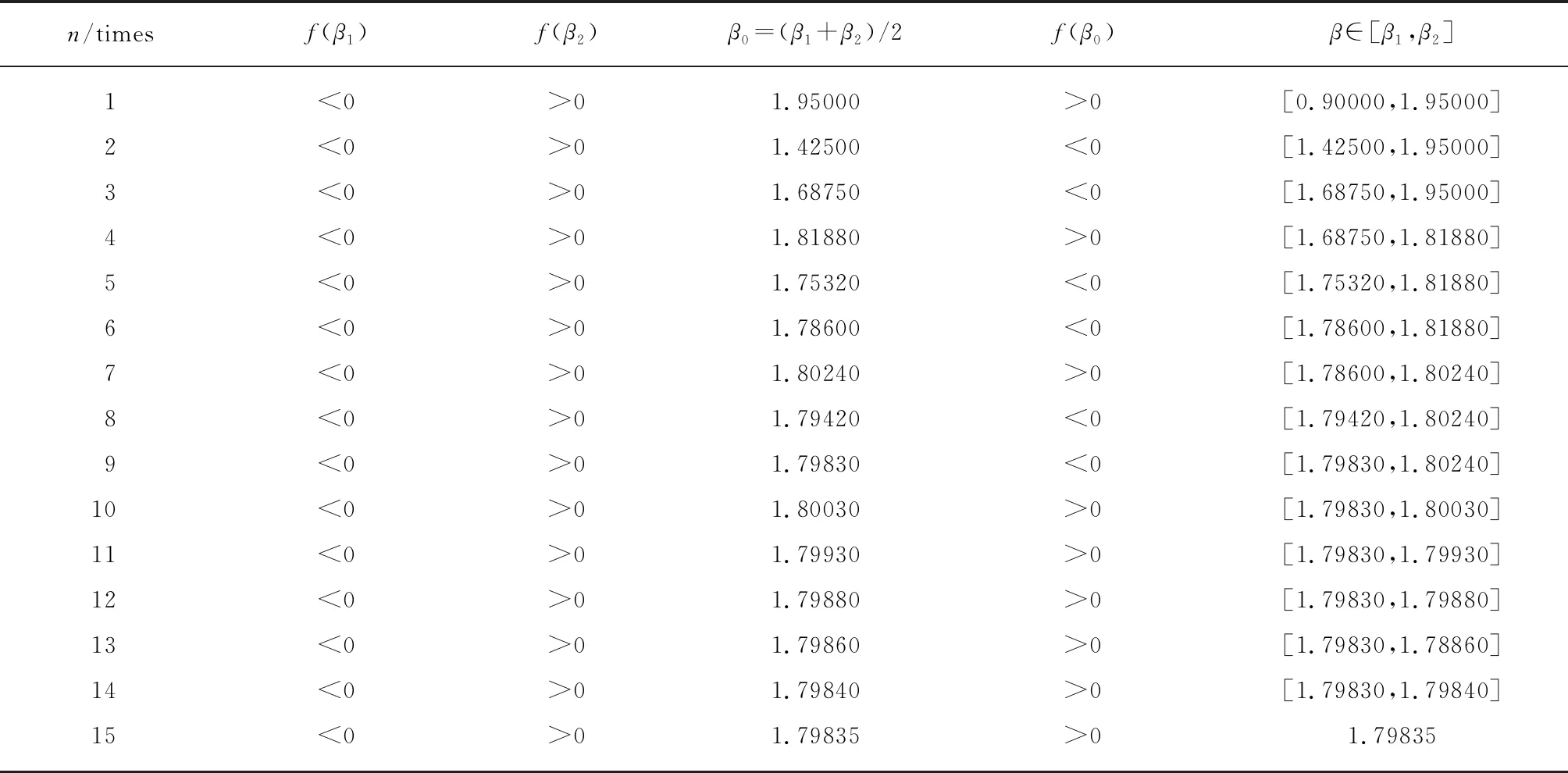
表8 迭代过程计算表Table 8 Iterative process calculation table

图7 涂层钢筋概率密度函数曲线Fig.7 Density function curves of coated steel bar

5 结论

(1)GEOMET涂层可以很好地保护氯氧镁水泥混凝土中的钢筋，防止其发生锈蚀；经过990d溶液加速浸泡试验后，涂层钢筋仍然处于轻微腐蚀状态.

(2)Weibull函数可以有效描述氯氧镁水泥混凝土中涂层钢筋的退化过程；基于电化学研究方法，以腐蚀电流密度作为退化指标，可以有效反映涂层钢筋的剩余寿命.

(3)在最小二乘法、矩估计法、最大似然法这3种参数估计方法中，最小二乘法比较适合描述小样本下涂层钢筋的耐久性退化过程，为涂层钢筋耐久性评估提供了可靠的参数估计方法.采用3种估计方法所得到的涂层钢筋最终失效时间都在38000d(104.1a)左右，且可靠度为0.4时所对应的失效时间R(t0.4)分别为2960d(8.1a)、12000d(32.9a)、21210d(58.1a).