PVA-ECC动态压缩性能研究

李 艳， 张文彬， 刘泽军

(河南理工大学 土木工程学院， 河南 焦作 454003)

建筑物在其使用寿命内不仅要承受静力荷载，也会不可避免地受到动态荷载，如强震区建筑结构的设计要考虑地震作用、国防工程中防护结构的设计要考虑抵御冲击与爆炸作用等.混凝土结构在承受动态荷载作用时，会表现出与静态荷载作用下不同的性能，因此混凝土材料的动态力学性能已引起国内外学者的广泛关注.相关研究表明，混凝土具有较强的应变率敏感性[1-2]，且混凝土材料在动态荷载作用下损伤软化效应十分明显[3-4]，这就限制了其在强震区与防护工程中的应用.

为改善混凝土材料的脆性，纤维混凝土应运而生.Zhang等[5]采用分离式霍普金森压杆(SHPB)试验研究了不同纤维体积分数和水灰比对聚丙烯纤维混凝土(PFRC)动态力学性能的影响，结果表明：PFRC的动态峰值应力、峰值应变、极限应变和韧性等均随着应变率的增大而增大；掺入聚丙烯纤维可有效提高材料的冲击韧性和抗裂性；当材料的水灰比较高时，试件的动态冲击韧性较好.Li等[6]基于玄武岩纤维增强混凝土(BFRGC)的SHPB试验，分析了纤维体积分数对BFRGC动态力学性能的影响，结果表明：玄武岩纤维的掺入对混凝土抗压强度的提高并不明显，但可显著改善其变形和能量吸收能力；当纤维体积分数为0.3%时，材料的动态性能最佳.叶中豹等[7]对钢纤维混凝土进行了动态压缩性能试验，发现随着纤维体积分数与应变率的增加，材料的动态峰值应力和峰值应变均明显提高.由此可见，纤维混凝土比普通混凝土具有更优异的动态力学性能.

高延性纤维增强水泥基复合材料(ECC)是基于微观力学设计，以水泥砂浆为基体，以体积分数不超过2%的随机分布短纤维为增强材料的一种纤维增强水泥基复合材料.ECC具有能量耗散能力强、极限拉应变大和韧性好等优点，成为近些年研究的热点[8-9].Chen等[10]对高炉矿渣微粉替代水泥后的聚乙烯醇纤维(PVA)增强ECC(PVA-ECC)进行了SHPB动态力学性能试验，结果表明：随着应变率的增加，峰值应力显著增加，峰值应变却有所减小；高炉矿渣微粉的掺量对材料增韧效果并不明显.Kai等[11]研究了PVA-ECC的冲击压缩性能，发现随着应变速率的增大，试件的动态峰值应力和峰值应变均增大，且动态强度增长因子(DIF)与应变率的对数近似呈线性增长关系.为进一步提高ECC的动态力学性能，Li等[12]在超高韧性水泥基材料(PVA-UHTCC)中掺入高弹模、高抗拉强度的钢纤维(SF)，并对SF/PVA-UHTCC进行了动态力学性能研究，发现钢纤维的加入可明显提高UHTCC的动态抗压强度和能量吸收能力，且当钢纤维体积分数为1.5%时，试件的动态力学性能最佳.杨惠贤等[13]的研究也发现，钢纤维的掺入可提高纤维增强水泥基复合材料的动态抗压强度，且在高应变率下，钢纤维体积分数的增大改善了材料的韧性.目前，国内外学者对PVA-ECC动态性能的研究相对较少，现有的研究主要集中在应变率对材料力学性能的影响，尚缺乏较为系统的研究，本文基于不同基体强度、不同PVA纤维体积分数PVA-ECC材料的SHPB冲击试验，研究了其在3种应变率下的动态压缩性能，主要分析了基体强度和PVA纤维体积分数对PVA-ECC材料动态压缩力学性能的影响，可以为PVA-ECC材料在抗震结构、抗冲击结构中的工程应用提供基础.

1 试验

1.1 试验设备和原理

采用直径为50mm分离式变截面霍普金森压杆，材质为钢，弹性模量210GPa，试验装置如图1所示.SHPB试验原理是基于一维弹性波假定和均匀性假定，采用三波法[14]计算试件的应变率、应力和应变.由于混凝土材料是脆性材料，在冲击作用下，容易在微小的应变下发生碎裂，此时应力波在试件中还未传播均匀，易造成试验结果出现明显误差，因此试验过程中采用波形整形技术[15]，在入射杆的端面加贴边长为1.5cm、厚度为0.3mm的黄铜片，以提高入射波的上升沿，使应力波在试件中传播 3～ 5个来回，进而保证试件应力均匀.冲击试验前，在试件2个端面涂抹少量凡士林，置于入射杆和透射杆之间压紧，以减少端面摩擦效应.

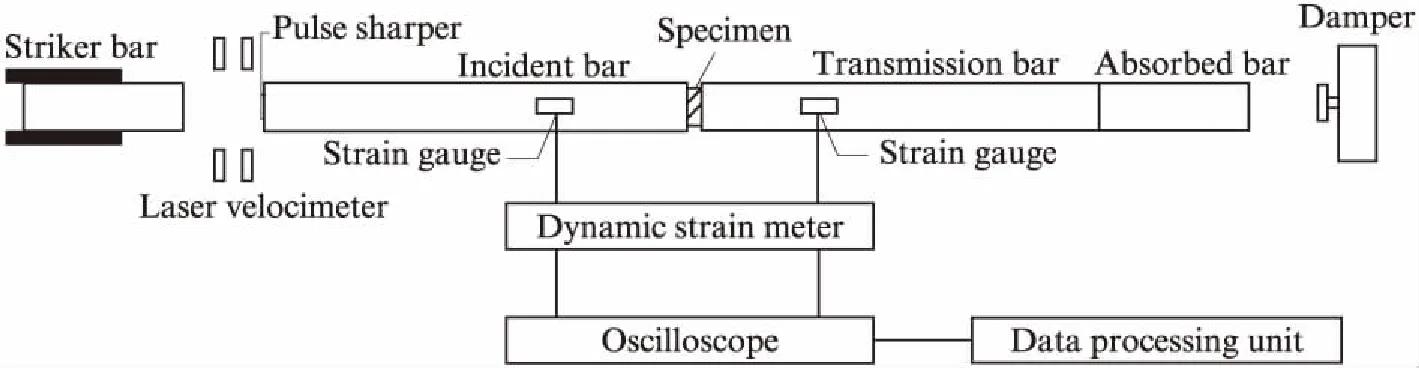
图1 SHPB装置示意图Fig.1 Schematic diagram of SHPB equipment

1.2 试验原材料与试件制备

P·O 42.5普通硅酸盐水泥；Ⅰ级粉煤灰；细骨料为天然细河砂，最大粒径0.6mm；减水剂为聚羧酸高效商用减水剂(减水率(1)文中涉及的减水率、水胶比等除特别说明外均为质量分数或质量比.为28%)；PVA纤维性能指标见表1.采用大掺量粉煤灰替代水泥来制备ECC，m(水泥)∶m(粉煤灰)=1.0∶1.2，砂胶比为0.36，为制备出不同强度的ECC基体，水胶比取0.32、0.36、0.40.PVA-ECC制备流程如图2所示.

表1 PVA纤维性能Table 1 Properties of PVA fiber

图2 PVA-ECC制备流程图Fig.2 Preparation procedure of PVA-ECC

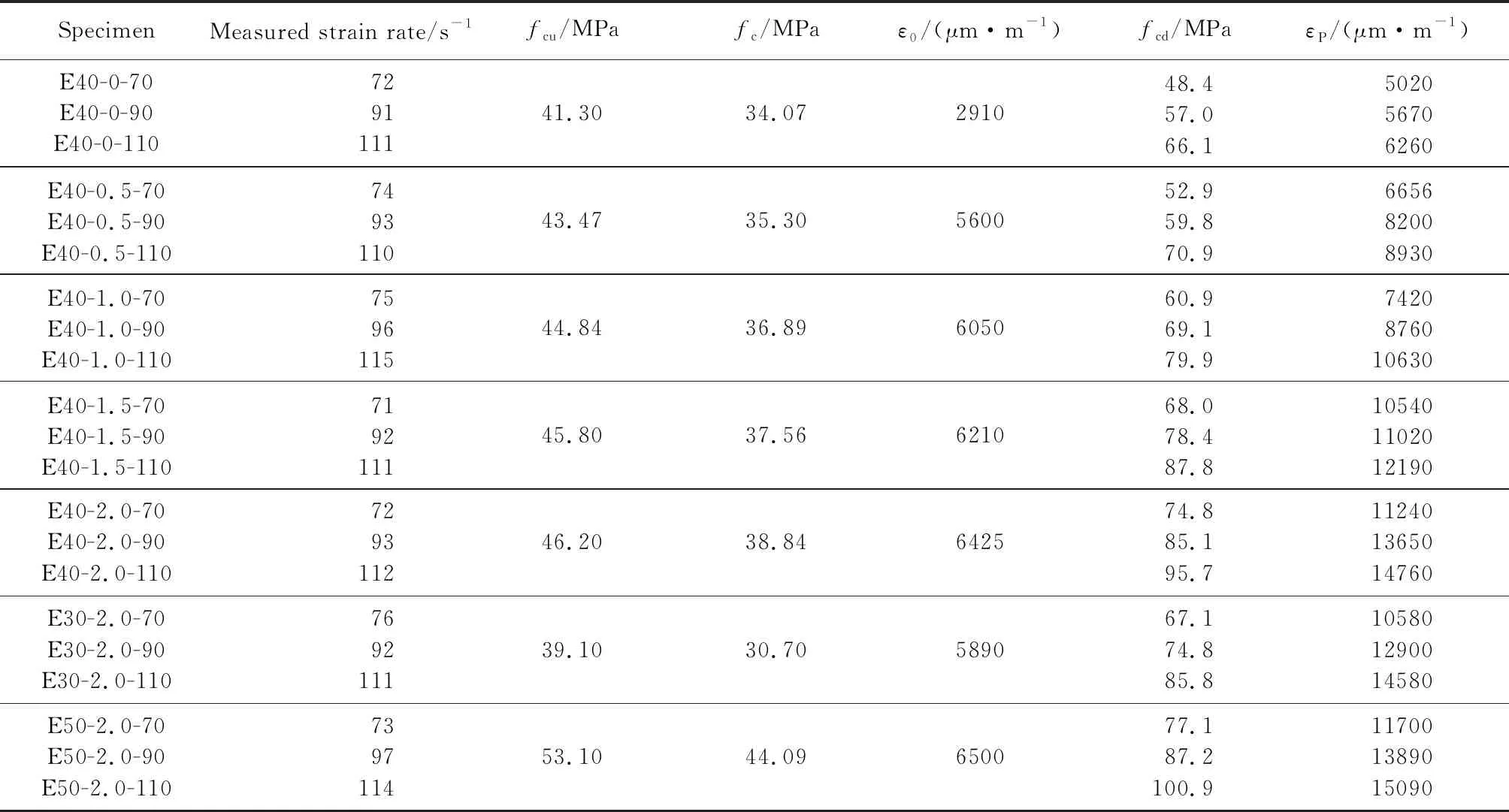
表2 试件参数与试验结果Table 2 Specimen parameters and test results

2 试验结果与分析

2.1 破坏形态

图3是PVA-ECC试件的典型破坏照片.由图3可见：应变率对试件破坏形态影响较大，即随着应变率的增大，试件中所产生的裂缝数量增多，PVA-ECC试件破坏后的整体性变差;未掺纤维的ECC基体试件在动态压缩荷载作用下呈现“碎块化”的破坏，试件破坏后的整体性很差(图3(a)～(c))；当PVA纤维体积分数超过0.5%后，在不同应变率作用下，PVA-ECC试件破坏的整体性均较好，且随着纤维体积分数的增加，由于纤维对裂缝的抑制作用增强，在相同应变率下，PVA-ECC试件中裂缝的数量和宽度明显减少(图3(d)～ (o))；当应变率与PVA纤维体积分数均相同时，随着ECC基体强度的提高，试件裂缝数量增多，但裂缝宽度减小(图3(m)～(u)).

图3 PVA-ECC试件的典型破坏照片Fig.3 Typical failure patterns of PVA-ECC specimens

2.2 动态应力-应变曲线分析

不同应变率下PVA-ECC试件的应力-应变曲线如图4所示.由图4可见：不同应变率下ECC的应力-应变全过程曲线具有一定的相似性；随着应变率的提高，材料线性阶段的范围增大，动态峰值应力和峰值应变均有所提高.图5给出了不同PVA纤维体积分数PVA-ECC试件的动态应力-应变曲线.由图5可见：在3种不同应变率下，未掺纤维的ECC基体试件动态峰值应变的平均值仅为0.57%，且其应力-应变曲线的下降段较为陡峭，试件的脆性破坏特征较为明显；掺入纤维后，由于PVA纤维可有效抑制裂缝的扩展，很好地发挥其“桥连”作用，PVA-ECC试件动态应力-应变曲线的下降段较为平缓，且在相同的应变率下，随着纤维体积分数的增大，试件的动态峰值应力和峰值应变均明显增大.图6给出了不同ECC基体强度PVA-ECC试件的应力-应变曲线.由图6可见：在相同应变率下，PVA-ECC试件的基体强度越高，其应力-应变曲线线性段的范围越大，试件的动态峰值应力越大，动态峰值应变也有增大趋势，但其提高幅度并不太明显；随着基体强度的增加，PVA-ECC试件应力-应变曲线的下降段变陡峭，试件延性变差.

2.3 动态峰值应力分析

由表2可见，当应变率从70s-1提高到110s-1时，试件E40-0.5、E40-1.0和E40-2.0动态峰值应力fcd分别提高了34.0%、31.2%和27.9%，即随着应变率的增大，PVA-ECC材料的动态峰值应力增大，表现出较强的应变率敏感性.这是由于：(1)在冲击荷载作用下，材料的惯性作用使试件侧向变形受到限制而近似处于围压状态，且应变率越高，这个限制作用越大[16-17]；(2)PVA-ECC材料在动态加载时，不再是沿单条或多条裂缝的扩展而破坏，而是同时产生大量微裂缝，尤其当应变率越大时，其所需能量就越多，再加上冲击荷载作用速度极快，材料没有充足时间用于能量累积，试件只能通过提高自身应力的方法来抵消外部能量[17].

图4 不同应变率下PVA-ECC试件的应力-应变曲线Fig.4 Stress-train curves of PVA-ECC specimens under three different strain rates

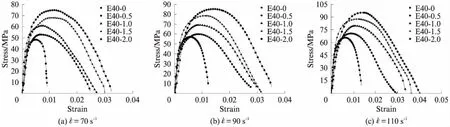
图5 不同PVA纤维体积分数PVA-ECC试件的应力-应变曲线Fig.5 Stress-train curves of PVA-ECC specimens with different PVA fiber volumn fraction

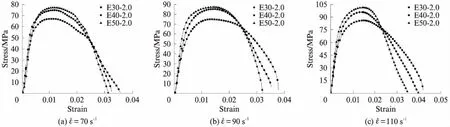
图6 不同基体强度PVA-ECC试件的应力-应变曲线Fig.6 Stress-train curves of PVA-ECC specimens with different matrix strength

表2还可见：在70s-1应变率下，当纤维体积分数从0%依次增加到0.5%、1.0%、1.5%、2.0%时，试件的fcd分别提高了9.3%，25.8%，40.5%，54.5%；在90s-1应变率下，试件的fcd分别提高了4.9%，21.2%，37.5%，49.3%；在110s-1应变率下，试件的fcd分别提高了7.3%，20.9%，32.8%，44.8%.由此可见，随着纤维体积分数的增加，其增强效果更明显，PVA-ECC的动态峰值应力显著增大.由表2可见：随着ECC基体设计强度的增加，材料的fcd增大，在70、90、110s-1应变率下，试件E50比E30的fcd分别提高了14.9%、16.6%和17.6%，这说明材料的动态峰值应力和基体强度也有较为明显的关系.

2.4 动态峰值应变分析

PVA纤维的加入提高了材料的变形能力，在静态受压时PVA-ECC材料的峰值应变ε0可稳定达到0.5%[18-19]；在动态受压时，PVA-ECC峰值应变εP的平均值约为1.05%(应变率分别为70、90、110s-1)，比静态平均峰值应变提高了110%.由表2和图4可见，当应变率从70s-1提高到110s-1时，试件E40-0.5、E40-1.0和E40-2.0峰值应变εP的平均值分别提高了34.2%、43.3%和31.3%.这表明随着应变率的增大，PVA-ECC材料的动态峰值应变也明显提高，表现出较强的应变率敏感性.其原因是PVA-ECC材料在动态加载时会出现大量微裂缝，而此时试件变形速度极快，裂缝并未贯通试件最薄弱界面，仅能在各自区域发展，故可提高PVA-ECC材料的变形能力[20-22]，因此峰值应变增大.由表2和图5可见：在70s-1应变率下，当纤维体积分数从0%依次增加到0.5%、1.0%、1.5%、2.0%时，试件的εP分别提高了32.6%，47.8%，110.0%、123.9%；在90s-1应变率下，试件的εP分别提高了44.6%，54.5%，94.4%、140.7%；在110s-1应变率下，试件的εP分别提高了42.7%，69.8%，94.7%、135.8%.这表明随着纤维体积分数的增大，PVA-ECC试件的动态峰值应变明显提高，即PVA纤维对PVA-ECC材料的动态增韧效果十分显著.由表2和图6可见，在70、90、110s-1应变率下，E50比E30的εP分别提高了10.6%、7.7%和3.5%，基体强度对PVA-ECC动态峰值应变的影响不太明显.

2.5 动态韧性分析

韧性是材料在荷载作用下具有的变形能力，是材料强度和变形的综合性能指标[23]，可采用应力-应变曲线所包围面积S的大小作为评价指标[24-25].图8为不同应变率下PVA-ECC试件韧性指标的对比图,其中SUP为上升段曲线所包围的面积，SD为下降段曲线所包围的面积，ST为全部曲线所包围的面积.由图8可见：PVA-ECC试件的韧度指标SUP、SD、ST均随着应变率的增大而增大；相同应变率下，随着纤维体积分数的增加，由于裂缝处有更多的纤维参与“桥连”，PVA-ECC试件的SUP、SD、ST也明显增大；应变率为70、90、110s-1时，试件E40-2.0比E40-0的SUP分别提高了259.7%，244.9%、234.2%，SD分别提高了533.1%，332.0%、277.9%，ST分别提高了392.9%，291.8%、257.7%.由此可见，同准静态压缩类似，PVA纤维对PVA-ECC材料峰后韧性的提高最为明显，但随着应变率的增大，纤维对PVA-ECC韧性的提高幅度均有所下降，其原因可能是由于较高应变率时，裂缝数量较多，试件在很短时间内损伤十分严重，使较多纤维更容易被拉断，因而纤维的增韧效果有所降低[12].相同应变率下，由于强度高的试件其内部更加密实，产生裂缝所需的能量就越多，由图8还可见：在70、90、110s-1应变率下，当基体设计强度由E30提高到E50，PVA-ECC试件的韧度指标SUP分别提高了23.5%，27.1%，25.4%；SD却分别降低了4.7%，19.0%，36.3%，这是由于低强度PVA-ECC的基体断裂韧度低[8]，更有利于PVA纤维的拔出而不是拉断，对提高试件的峰后延性是非常有利的，尤其在高应变率下，低强度基体对试件峰后韧性的改善更加明显.

图8 不同应变率下PVA-ECC试件韧性指标的对比Fig.8 Comparison of toughness index of PVA-ECC specimens under different strain rate

3 结论

(1)PVA纤维的增韧、阻裂作用可有效改善PVA-ECC试件的冲击破坏程度，当纤维体积分数超过0.5%后，在3种应变率下，试件均未出现“碎块化”的破坏模式，且纤维体积分数越大，试件冲击破坏时的整体性越好.

(2)PVA-ECC具有较强的应变率效应，随着应变率的增大，PVA-ECC材料的动态峰值应力、峰值应变和韧性均明显提高.动态强度增长因子DIF与应变率的对数呈线性增长关系.

(3)随着PVA纤维体积分数的增大，PVA-ECC的动态峰值应力、峰值应变和韧性增大，且PVA纤维对PVA-ECC峰后韧性的提高最为明显，但对PVA-ECC抗压强度应变率敏感性的影响较小.

(4)提高ECC基体设计强度，PVA-ECC动态峰值应力增大，但动态峰值应变提高不明显，且基体强度高的PVA-ECC峰后韧性明显降低，而基体强度对PVA-ECC抗压强度应变率敏感性的影响不太明显.