基于置信规则库的机载导弹故障诊断

刘兆政， 肖明清， 朱海振， 李剑峰， 张 磊， 杨亚军

(1.空军工程大学航空工程学院， 西安， 710038； 2.国防大学联合勤务学院， 北京， 100858；3. 95910部队， 甘肃酒泉， 735018)

机载导弹故障诊断是使导弹处于良好战备状态，发挥其作战效能，完成空中作战任务的重要保证。随着高新技术在机载导弹上的运用，机载导弹性能不断提升的同时，也增加了系统的复杂性，涉及到机械、电子、计算机等多个领域[1]，而装备越复杂，故障诊断任务就越繁重，诊断难度也就越大[2]。在这种情况下，准确地诊断并隔离各种故障对于提高导弹的完好率和作战效能具有重要意义[3]。

目前，国内外对故障诊断技术进行了大量研究，主要可分为基于数据驱动的故障诊断技术和基于模型的故障诊断技术两大类。基于数据驱动的故障诊断技术主要包括：BP神经网络[4]、粗糙集方法[5]、主元分析法[6]等。此类方法主要依赖历史数据，对历史数据的质量要求较高，但在实际故障诊断过程中，由于导弹本身具有可靠性高、可长期贮存、一次使用的特点，故障率比较低，故障样本较少，可能会造成数据不平衡，因此不适合用数据驱动的方法。基于模型的故障诊断方法相关研究成果主要包括基于物理模型的故障诊断技术和基于经验模型的故障诊断技术[7]。这类方法的优点是不完全依赖数据，能够克服数据驱动的方法造成的过拟合问题，缺点是诊断精度依赖专家的经验知识[8]，如果专家构建的模型不准确，必然会导致诊断结果不准确。同时，由于受专家对专业领域知识了解程度的影响，专家的判断具有很大的主观性，也不一定完全可靠。

针对上述问题，本文提出利用基于证据推理的置信规则库(Belief-rule-base Inference Methodology Using the Evidential Reasoning Approach，RIMER)推理方法[9]进行机载导弹故障诊断。该方法能够综合利用主、客观信息且可调参数物理意义明确，是专家知识及数据驱动方法的结合[10]。置信规则库能够通过参数优化减小专家知识中主观偏差的影响，同时在专家知识的基础上进行数据训练，对其中专家设定的参数进行调整。

1 基于证据推理的置信规则库推理方法

1.1 置信规则库结构

置信规则库规则的一般表达形式为：

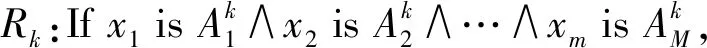
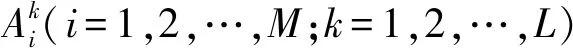
1.2 置信规则库推理

置信规则库的推理首先需要计算激活权重，然后使用证据推理算法集成激活的规则。激活权重ωk指根据匹配度、规则权重及属性权重计算出的规则对输入的参考程度。激活权重计算方法为：

(1)

(2)

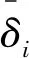
O(X)={(Dj,βj);j=1，2，…，N}

(3)

式中：βj为后项Dj的置信度，表示为：

(4)

式中：u为效用值，表达式为：

(5)

1.3 置信规则库优化学习模型

置信规则库中的前提属性权重、规则权重、结果置信度均由系统专家根据经验设定，具有一定的主观性。为了选取置信规则库的最优参数，Yang提出了对置信规则库参数优化的基本思想[9]。置信规则库优化学习模型具体结构见图1。

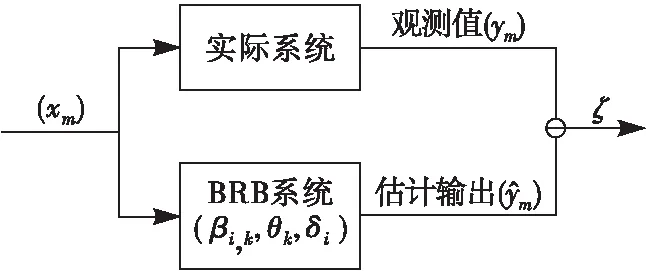
图1 置信规则库优化学习模型

此外，为了获得性能更好的置信规则库，将前项属性Ai,j及后项属性Dj的参考值纳入优化范围，添加到上述优化学习模型中，利用Matlab中的Fmincon函数对初始置信规则库的参数进行优化。Fmincon是用于求解非线性多元函数最小值的matlab函数，优化工具箱提供Fmincon函数用于对有约束优化问题进行求解，其语法格式为：

x=Fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

式中：x0，b，beq，lb和ub为线性不等式约束的上、下界向量；A和Aeq为线性不等式约束和等式约束的系数矩阵；fun为目标函数；nonlcon为非线性约束函数，用options参数指定的参数进行最小化。

2 基于置信规则库的机载导弹故障诊断

图2 故障诊断流程图

2.1 基于模糊语义值的输入信息转化

针对模块选取不同参数作为输入，利用专家知识处理参数。专家知识往往以语义的形式表达，具有模糊性，而实际的测试保障过程中可以通过传感器得到导弹电流、电压等参数，想要利用专家知识处理相关参数，需要先设定语义值及其参考值，再计算匹配度完成数值到语义值的转换。

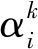
当xi≤Ai,1或xi≥Ai,Ji时，xi对于Ai,1或Ai,Ji的匹配度为1，对其他参考值的匹配度均为0；当Ai,q≤xi≤Ai,q+1(q=1,2,…，Ji-1)时，xi对于Ai,q和Ai,q+1的匹配度计算方法见式(6)～(7)，对其他参考值的匹配度为0。

ai,q=(Ai,q+1-xi)/(Ai,q+1-Ai,q)

(6)

ai,q+1=(xi-Ai,q)/(Ai,q+1-Ai,q)

(7)

此外，在导弹故障诊断过程中，往往包含定性信息和定量信息。噪声电压过大是一种定性信息的模糊判断，可以用一个模糊值将噪声电压数值映射到噪声电压“大”[13]。例如在导弹制冷系统中对于噪声电压，定义一个“非常大”的隶属函数，见图3，其中a=0 mV，b=100 mV。如果测量得到的噪声电压为97 mV，此时即可转化为上述语义表达方式。

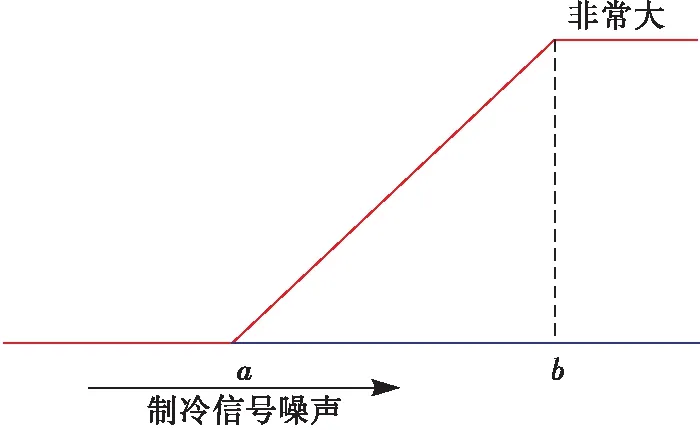
图3 隶属函数

在这种情况下，输入xi的参考值Ai,q(i=1,2,…,M；q=1,2,…,Qi)为模糊形式的语义值，采用基于隶属函数的方法，把以上形式的定量输入信息xi转化为Ai,q的置信度αi,q，即：

(8)

式中：0≤αi,q≤1；τ表示匹配函数。令τi=τ(xi,Ai,q)，且τi表示匹配度，如果xi完全属于第q个语义值，则τ(xi,Ai,q)=1，基于归一化的匹配度τi和置信度εi，产生置信度αi,q。由于εi的存在，αi,q可能不等于1。

2.2 基于独热编码的参数优化

在计算出基于模糊语义值的匹配度之后，再经过1.2节中介绍的证据推理过程，可得出后项置信度β。针对结论数据表现为离散的属性特征值，本文对置信规则库的后项结论进行独热编码，将原本离散的属性特征扩展至欧式空间。根据编码的特征可知，不同结论数据间编码的距离均相等，符合分类问题中数据属性重要性相同的特点[14]。

例如针对制冷系统故障编码方式见表1。

计算数据间的欧式距离E(D)：

首先，安排专门的施工人员针对孔内水头情况进行全面细致的观测，保证孔内的水头高度能够符合相应的工程施工标准，发现孔内的水头相较于孔外水头较低，则需要及时将泥浆池中的泥浆抽取到孔内，减少钢护筒在外力作用下出现变形情况。其次，在施工现场做好黏土的准备工作，及时向孔内充填黏土，待回填至护筒底以上5m高度后，停止回填黏土。

(9)

以系统输出与实际输出的欧式距离为参数优化目标函数：

(10)

表1 置信规则库输出项及其编码

2.3 累积误差

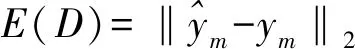
(11)

简而言之，根据专家对导弹结构参数和故障位置的非线性复杂关系的认识，结合对导弹故障数据的分析，给出规则的前项参考值、属性权重和规则权重、后项置信度这一系列参数，即可建立初始置信规则库，并进行相关参数优化和误差指标选取。

3 实例分析

3.1 实例背景

以某型机载导弹制冷系统的故障诊断为例，对本文提出的基于置信规则库的故障方法进行阐述，并对其有效性进行验证。制冷系统是该型机载导弹红外导引头的一个关键部件，一般由制冷器、探测器、过滤器和管道等构成[15]，主要用于在探测目标前进行制冷，将探测噪声降到合理水平[16]。

制冷故障是该型导弹常见的一种故障，指启动制冷后，在规定时间内探测噪声无法降到规定的水平之内。根据专家的经验，故障的推理大概有以下几种情况：①探测器故障：尽管温度降下来，但是制冷信号的噪声电压没有下降，比理论值高很多，而制冷流量没有大幅下降；②制冷器故障：制冷信号的噪声电压在制冷后有些下降，比理论值略微偏大，但制冷流量没有大幅下降；③氮气管路故障：制冷信号的噪声电压在制冷后有些下降，制冷流量出现大幅下降。

由此可得与制冷有关的参数主要包括制冷信号噪声电压和制冷流量。本文以制冷信号噪声电压和制冷流量为输入，对制冷系统的故障位置进行诊断。为了使用专家知识，依据专家定义的模糊数据类型，对参数进行模糊化处理。

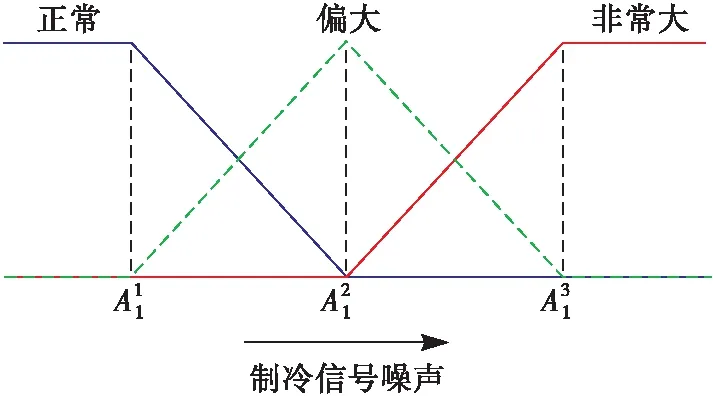
图4 制冷信号噪声的隶属函数

图5 制冷流量的隶属函数

经模糊数据处理后，部分数据展示见表2。

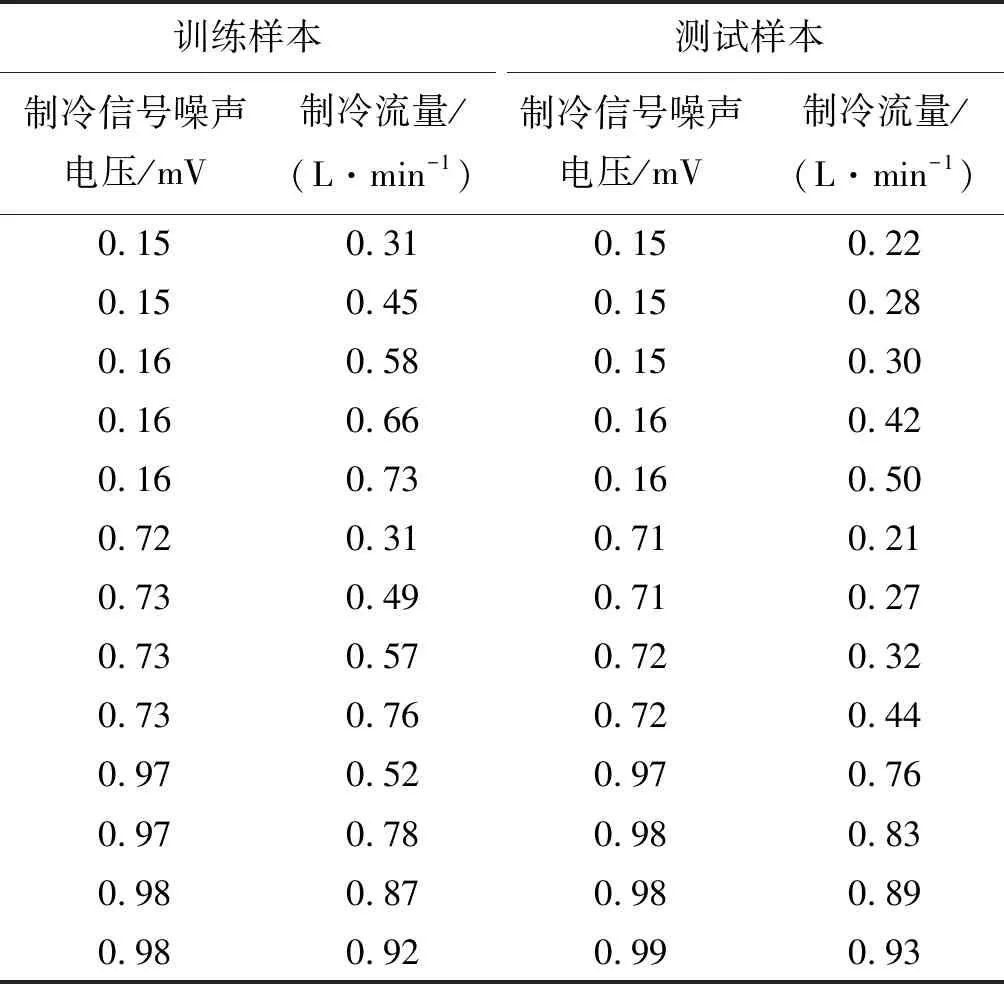
表2 部分实验数据

3.2 置信规则库建立

根据制冷系统的工作特性、测试数据及专家经验等信息，进行语义值及其对应参考值的设定。针对制冷系统故障诊断问题，前项属性制冷噪声电压和制冷流量选取3个参考值。制冷噪声电压语义值描述分别为：正常N(Normal)、偏大L(Large)、非常大VL(Very Large)。制冷流量语义值描述分别为：非常小VS(Very Small)、偏小S(Small)、正常N(Normal)。在此基础上，根据专家对其外部特性参数与制冷系统各部件之间的非线性复杂关系的认识，结合对脱密后的数据分析，建立初始置信规则库见表3。

对于置信规则库后向输出，采用独热编码对具体故障位置进行表述，如表1。其中，属性权重δ1，δ2均取值为1。

3.3 置信规则库优化

为减少初始置信规则库中包含的主观偏差，利用1.3节中提到的优化方法对初始置信规则库进行优化。形成优化后的置信规则库见表4，其中优化后的属性权重取值为δ1=0.216 5，δ2=0.639 2。

优化后的规则权重从规则1到规则9分别为：0.000 6，0.072 9，0.670 3，0.753 2，0.006 2，0.022 9，0.769 3，0.091 6，0.334 7。优化后的前项参考值见表5。

3.4 对比分析

本文选用均方误差MSE、均方根误差RMSE和平均绝对误差MAE对诊断效果进行对比，距离越小表示诊断结果越贴近于实际情况，误差越小，诊断效果越好。

选取欧氏距离和曼哈顿距离，利用训练数据对置信规则库的制冷故障诊断效果进行误差分析，求出优化前和优化后的MSE、RMSE和MAE。对训练数据的诊断结果误差见图6～7。

图6 置信规则库优化前后效果对比(曼哈顿距离)

图7 置信规则库优化前后效果对比(欧式距离)

从图6中可以看出，优化后的置信规则库距离较小，即对训练数据的诊断效果较好，其误差对比见表6。

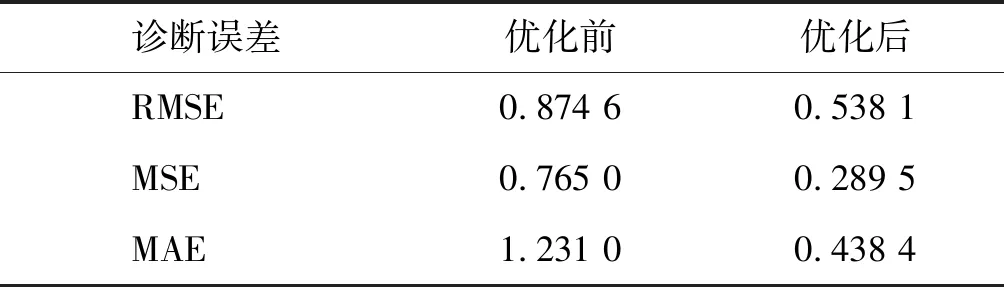
表6 故障诊断误差对比

由于置信规则库参数的训练结果具有随机性，本文利用另一组测试数据进行验证，得到测试数据优化前后的欧式距离和曼哈顿距离对比，见图8～9。

图8 测试数据误差对比(曼哈顿距离)

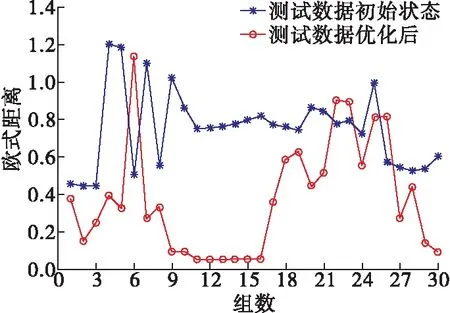
图9 测试数据误差对比(欧式距离)

从图中可见，初始置信规则库的测试效果误差较大，经过参数优化后的置信规则库诊断效果较好且较为稳定，故障诊断准确率较高，对应的RMSE、MSE和MAE较小，在本文系统环境下(CPU: Intel (R) Core (TM) i5-6300H，主频2.3 GHz，RAM 4.0 GB)，针对制冷电压噪声输入，对比初始置信规则库运行响应时间为223 ms，优化后的置信规则库为76 ms，故障诊断实时性较好。

建立3层BP神经网络，其中输入层包含2个节点，分别为制冷信号噪声电压和制冷流量。输出层节点数为1，为制冷系统故障诊断概率。隐含层采用tansig函数，隐含层节点个数基于对系统精度的考虑，选取为25。设置最大迭代次数1 000，训练目标误差0.001。

利用训练数据对网络进行训练。在算法实现的过程中，设置提前停止(Early Stopping)，在训练过程中，记录到目前为止的最佳精度，对优化后置信规则库方法及神经网络的训练结果进行验证，记录两者对测试数据的累积误差，见图10。

针对不同故障位置，统计2种方法的故障诊断准确率，见表7。

从图10、表7可以看出，优化后的置信规则库方法诊断的误差要低于神经网络，且优化后故障诊断准确率较高。经计算，对于测试数据，神经网络算法的累计误差为2.606 7，优化后置信规则库的累计误差为2.049 9，可见优化后的置信规则库的故障诊断精度较高。

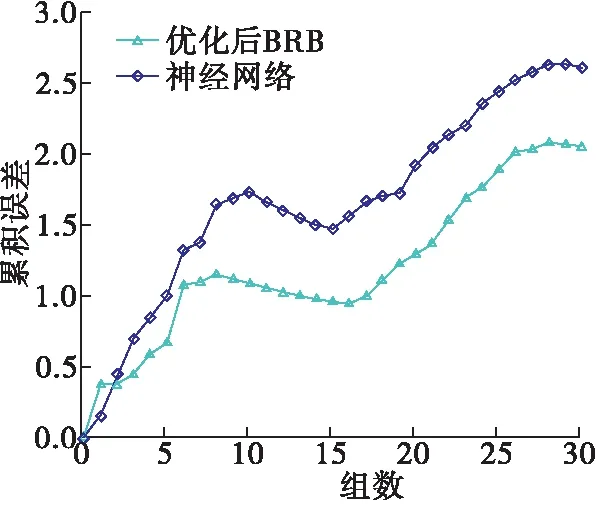
图10 测试数据累积误差对比

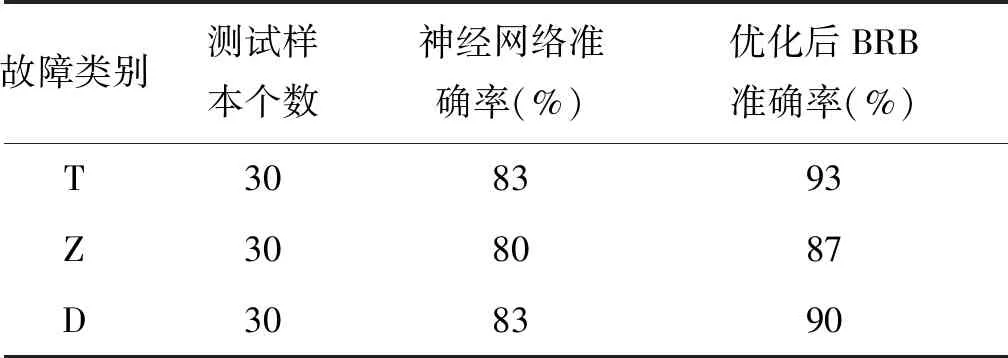
表7 故障诊断准确率对比

4 结语

本文提出了基于置信规则库的机载导故障诊断方法。利用专家知识建立初始置信规则库，对故障位置进行独热编码，并通过历史故障数据对初始置信规则库进行优化。以机载导弹制冷系统为例，利用模糊数据类型对故障数据进行处理，测试数据表明优化后的置信规则库在故障诊断方面效果较好。该方法不仅能够有效利用专家的经验知识，还能将系统中的不确定信息量化，使得模型更贴近系统的真实情况。实验结果表明该方法切实可行，能在实际故障诊断过程中为机载导弹的维护保障工作提供参考。