安徽省人口结构预测模型的构建及应用
——以宿州市为例
高凤伟,武以敏,李壮壮,李 强
(1.宿州学院 数学与统计学院,安徽 宿州 234000;2.宿州学院 统计调查咨询中心,安徽 宿州 234000)
人口是一种资源的说法被越来越多国家接受,各国都有对人口做过调查与预测。新加坡曾出台过《人口政策白皮书》,英国、美国等也在国家层面上制定人口战略,而我国也实行每10年的人口普查制度。对人口的预测方法也多种多样,人口预测模型也各有优劣。例如李晓梅的《人口预测模型研究及应用》[1]、王桂新的《区域人口预测方法及应用》[2]等。宿州市作为皖北典型城市,经济发展水平较其他地方落后,人口的发展又影响着经济的发展,在我国全面实施二孩政策背景下,宿州市的人口如何发展,人口结构又该如何变化。本文立足地区现状,首先用经典人口预测模型对宿州市人口未来变化进行预测,并结合实际情况对模型采用优化组合,最终得出新的人口预测模型。
1 人口发展模型的构建
1.1 宿州市人口logistic 增长模型
1.1.1 模型介绍[3]
Logistic 模型是1938年Verhulst-Pearl 在修正非密度方程时提出的,他认为实际增长率不是内禀增长率,而是在一定的环境中种群的增长总存在一个上限,当种群的数量逐渐向着上限上升时实际增长率就要逐渐地减少,因而也称Verhulst-Pearl 方程
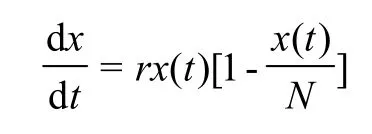
式中:x(t)表示t时刻的人口数量;r是人口的内禀增长率(即增长率-死亡率);N为环境能容忍的最大人口数量。
1.1.2 模型构建[4-5]
运用微分方程的分离变量法,对logistic 模型的解析解为
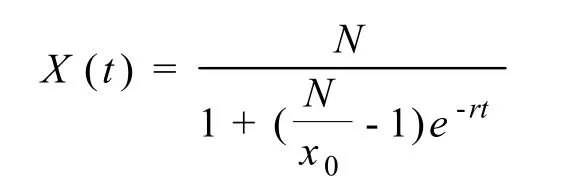
数据取自2000~2014年宿州市人口数据(令2000=1,2001=2,…,2014=15,分别赋值t=1,2,…14),为估计模型中的未知系,现取2000年、2005年、2010年3组等间距数据。;代入公式


运用logistic 模型预测宿州市2010~2015年人口数,预测结果如表1。

表1 宿州市logistic 模型预测误差
由表1,运用logistic 模型预测相对误差较小,均在3%以下,说明logistic 模型可较好预测宿州市人口增长,则可用于宿州市人口的短期预测。
1.2 宿州市人口发展模型的构建
1.2.1 模型介绍及数据选取
人口发展遵循其固有的规律,受系统内部各影响因素的制约,因此本文选用宋健等人提出的人口发展模型对宿州市人口进行预测[6]。模型结构如下:
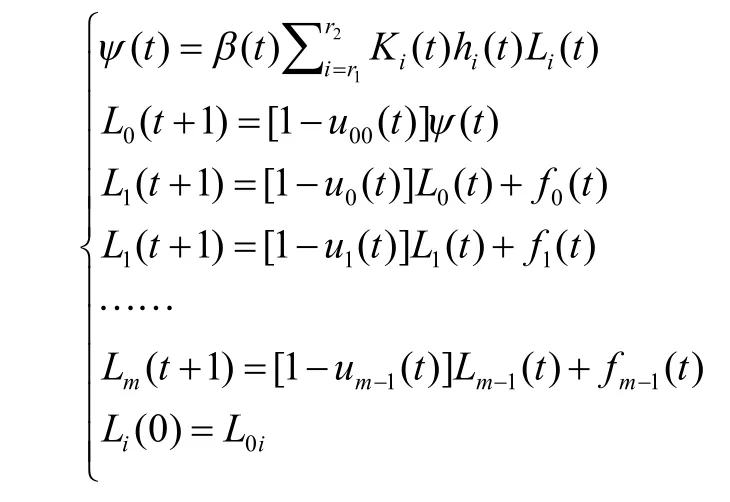
预测每年总人数为:

式中:m为预测系统内的最高年龄,此处选100 岁为预测的最高年龄;r1,r2分别为育龄妇女的起止年龄,此处选r1为15岁,选r2为50岁;Li(t)(i=0,1,2,…,m)为t年满i岁不满i+1 岁的人口数,ui(t)(i=0,1,2,…,m)为t年i岁年龄组的死亡数;Ψ(t)为t年婴儿总数;Ki(t)为t年i岁年龄组的女性比;hi(t)为t年i岁年龄组生育因子,应满足,生育因子显示了各年龄段育龄妇女的生育现状,某一年龄组的生育因子越高代表该年龄组相对于其他年龄组的生育率越高,此处的生育因子数据选取通过λ2分布获得;u00(t)为t年婴儿死亡率;fi(t)为t年i岁系统环境相对扰动人口数;β(t)为t年总和生育率。所需数据均取自宿州市统计年鉴及宿州市2010年人口普查数据。
根据宋健等学者的研究,模型中生育函数hi(t)可用λ2分布密度曲线来表达,由于国家对计划生育政策逐步放开,从2010年开始各省开始实施单独二孩政策[7],故计划生育政策的放宽将影响生育函数,宿州市2010年育龄妇女的生育率状况如图1。

图1 宿州2010年育龄妇女的生育率
由图1,宿州市的育龄妇女在23 岁左右生育率最高,故取峰值生育年龄i0=23(n=10)。
2010年后,随着单独二胎政策放开,可预见峰值生育年龄将提前,结合实际情况和《婚姻法》的相关规定,二胎政策全面放开后,取宿州市的峰值生育年龄i0=21(n=8),带入生育函数hi(t),可得全面二孩政策启动后各生育年龄生育因子[8],如表2。
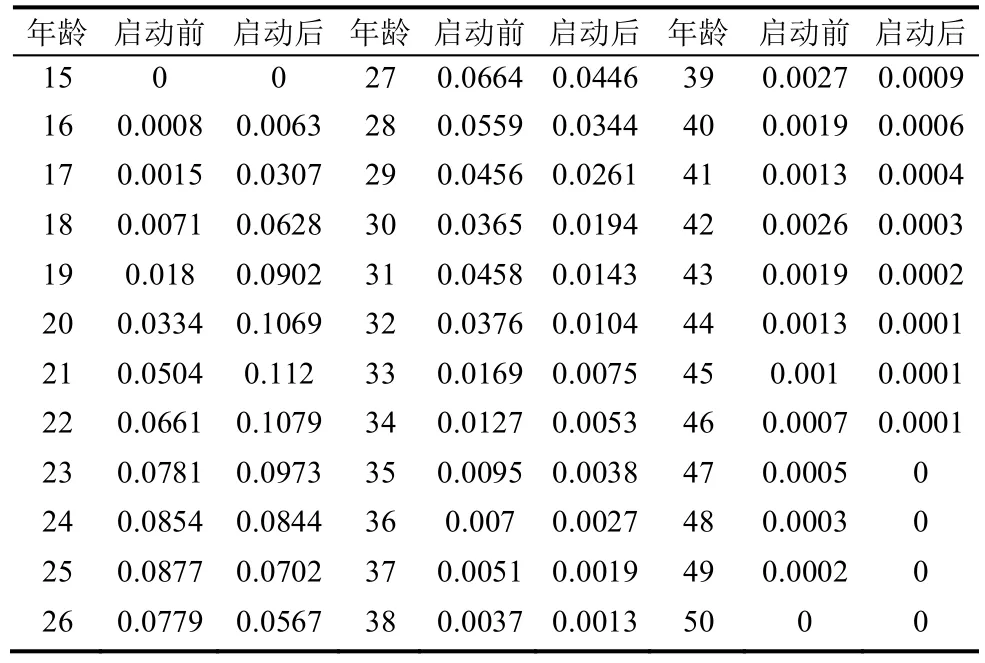
表2 二孩政策放开前后hi(t)变化值
2016年全面放开二孩政策,但在生育函数中宿州峰值生育年龄在2010年已取21 岁,根据《婚姻法》对法定结婚年龄最低限制,无论生育政策如何放宽宿州市生育函数中峰值生育年龄也难以降低。因此沿用2010年政策启动后的生育因子值。

1.2.2 模型论证
通过对人口发展模型的优化得最终模型,用此模型对宿州市2013 至2018年预测,结果如表3。
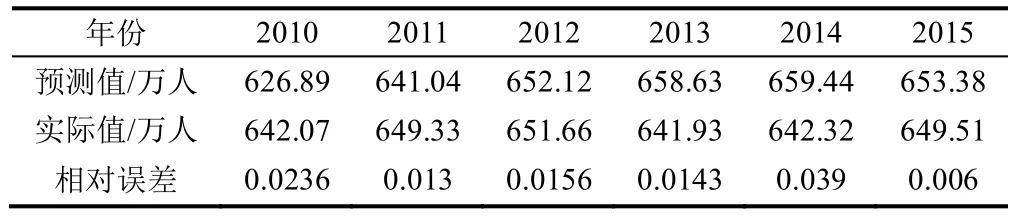
表3 人口发展模型(户籍人口)预测结果
由表3,人口发展模型的预测值与真实值之间相对误差不超过4%,故该模型对宿州人口未来增长有较可靠的预测,最终预测结果如图2。

图2 修正后人口发展模型(户籍人口)预测走势
由优化的人口发展模型知,该模型对宿州市的未来短期的预测口增长不明显,但长期来看宿州市人口呈现不断增长趋势,增长速度近期有所提高。
2 模型优化组合
选用的两模型各具优势,因此尝试将两种模型优化组合形成新的组合模型,保留各自模型优势减少预测误差,对模型优化组合分为短期预测和长期预测两个阶段。在组合优化模型中同样沿用2023年为长短期分界点,在2023年以前为人口短期预测,在2023年以后为人口长期预测。
2.1 短期的优化模型预测
构建线性组合预测模型[9]

式中,令yt1为logistic 模型预测结果,W1为其权重,令为yt1的残差平方和;y2t为人口发展模型预测结果,W2为其比重,为y2t的残差平方和,将模型的残差方差作为其比重计算标准,即残差方差越大,比重越小,令。将上文中模型结果,带入上式得短期预测模型:
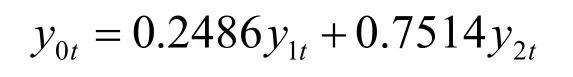
运用组合优化模型得到的预测值与实际值比较,如表4。

表4 组合优化模型得到的预测值与实际值
由表4 知组合优化模型从2005年到2015年的预测值与真实值的相对误差比logistics 预测模型与人口发展模型预测的相对误差更小,说明组合优化模型的预测值更精确。则组合优化模型对宿州市2019年-2023年人口预测如表5。由预测结果知,短期内宿州市人口的增长规模在原有基础上稳步上升。在宿州市人口生育峰值并没有提前的基础下,宿州市人口规模呈现稳步上升趋势,表明宿州市劳动力及老年人口有所增加,短期宿州市人口特征的变化规律较慢。而宿州市人口长期的变化趋势及各年龄段人口数变化可由人口发展模型得出。

表5 宿州市人口短期组合优化模型预测值
2.2 长期优化模型预测
2.2.1 长期预测模型构建
由于Logistic 模型较适用于短期预测,因此不参与宿州市人口的长期预测;而人口发展模型是基于各年龄组育龄妇女的生育率等内生因素,模型所依赖的变量影响较明确且具体详细,其预测结果具有长期性,能在长期内达到较好的预测效果,因此对宿州市人口未来长期预测主要采用人口发展模型预测。长期内对宿州市总人口增长预测公式截取为[10]:
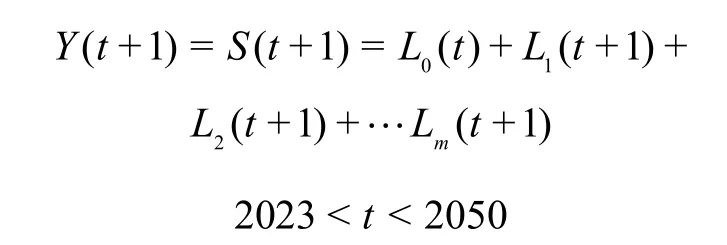
由于人口模型特殊的模型结构,通过人口发展模型不仅能够预测宿州市总人口数,同时还能对宿州市各年龄组的人口数Li(t)进行预测,这对宿州市的人口劳动力变化趋势及人口老龄化程度的研究具有重要意义。由以上所设定的人口发展模型最终预测结果如表6 所示。

表6 宿州市人口发展模型预测结果
2.2.2 预测结果分析
表6 数据显示,宿州市总人口平均以0.011%的增长率低速增长,该增长率是以每年新增10 万左右的婴儿数为基础的,每年的新增婴儿数平均维持在10 万名水平,随着全面二孩政策的放开,未来几年新增婴儿数将会在此基础上有所增加;21~65岁的劳动力人口比重却逐年递减,这一结果源于20世纪八九十年代我国的计划生育政策,使得生育率降低,持续的低生育率致使迈入20 岁左右的劳动力人口增长速度远远低于迈入老年人口的比重;图3 显示了宿州市0~20 岁青少年人口比重逐年下降,也是由于近年来低迷的生育率使得青少年的比重在总人口中比例下降;而66 岁以上的老年人比重逐年递增,这也是我国经济发展的必然结果,医疗卫生水平,生活水平的上升,使人们的寿命延长;按照测算 2024年宿州市老龄化人口比重达到13.04%,根据联合国《人口老龄化及其社会经济后果》确定的划分标准,当一个国家或地区65 岁及以上老年人口数量占总人口比例超过7%时,则意味着这个国家或地区进入老龄化,宿州的这一比例远远大于标准,这表明宿州市早已进入了老龄化社会。

图3 宿州市人口预测趋势图
3 结论与建议
研究表明,未来很长一段时期,宿州市的人口将呈现低速发展阶段,且每年的新增人口数远远小于迈入老年人行列的人口,致使宿州市老龄化社会加剧,劳动力人口逐年下降,老龄人口逐年上升。
纵观全文和对宿州市未来人口增长预测,宿州市政府要提前做好相关人口保障准备[11]。完善宿州市基础设施与养老保障,建立多层次、多级别的养老机构,鼓励发展民营高水平养老机构提供个性化养老服务与政府发展基础性服务相结合;开展多元化养老模式,家庭养老、社区养老、居家养老各模式相互补充,特别要解决好“失地”人群的养老问题;政府要尽快建立养老服务标准,规范养老市场秩序,维护老年人权益;面对劳动人口比重的下降,政府要加快产业结构调整,鼓励劳动密集型产业升级转型,引进先进生产技术与设备,预防陷入“人口诅咒”的陷阱。

