理趣相生：构建深度学习的小学计算课堂

（福安市实验小学南湖校区，福建 宁德 355000）

在小学数学教学中，计算教学是基础。但很多教师认为计算课枯燥无趣，思维含量低，只要学生能够套用算法，细心计算，多加练习，就能提高正确率。针对这些问题，如何强化教学设计，提高学生学习兴趣，构建计算深度学习课堂呢？

一、创设情境，引导领会算理

新课程提倡“让学生在生动具体的情境中学习数学”，就是要重视数学教学的生活化，将抽象的算理直观化和具体化。例如，苏教版四年级下册的混合运算第一课《不含括号的三步计算式题》，在例题教学时，可创设在超市购物的情境：

1.出示情境。从图中你知道了哪些数学信息？放在购物车中商品有多少钱呢？妈妈写了这样一道综合算式（出示：10×3+20×4）根据这个算式，想想他们购物车里放了什么。

2.辨析算式。这些商品一共多少钱呢？你们来当当裁判，到底谁算得对呢？

大大：10×3+20×4 小小：10×3+20×4

=30+20×4=30+20×4

=30+80=50×4

=110（元）=200（元）

学生根据情境和已有的学习经验，很快能判断出大大的做法是正确的。

3.理解算理。让学生和同桌交流，再在作业单上写想法。有了情境的依托，学生很快写出自己判断的理由。如以下三个学生的判断理由：

生1：我支持大大，因为买3 盒水彩笔的价钱和买4 盒曲奇饼干相加起来，所以要分别算出彩色笔的价钱和饼干的价钱再相加。

生2：因为买的是两种商品，所以要分别算出两种的价钱再相加。

生3：

……

接着，师再出示：100+24÷4×2，这道题的背后也藏着一个购物车的故事。根据算式，想想妈妈又挑了哪两样商品放在购物车里?

创设数学情境，是呈现给学生刺激性的数学信息，引起学生学习数学的兴趣，启迪思维。［1］在上述教学案例中，根据算式来反向思考购买了哪些商品，提升了思维难度。学生在交流讨论中，明确应该选择的商品，用生活经验解决数学问题，符合儿童学习数学的认知规律。同时，打破计算课枯燥无趣的教学模式，使学生能够在课堂上快乐地深度学习。

二、沟通知识，启发感悟算理

数学教材的知识是一个体系，具有很强的关联性，在执教过程中，要注意新旧知识的勾连，要从单元整体乃至课程的角度去设计课堂，使学生对算理产生深刻认知。例如，在执教苏教版数学五年级上册《小数的加法和减法》时，让学生先估算4.65+3.2，在此基础上，动笔列出竖式计算。此时，教师提出思考：“为什么要把小数点对齐来列竖式呢？”学生一致认为，是因为小数点对齐，相同的数位才对齐时，教师追问：“为什么要把相同数位对齐？为什么只有相同数位上的数才能直接相加减呢？”引导学生回顾学习的整数加减法的方法与小数的意义，理解十分之几只能和十分之几相加，几个一只能和几个一相加……学生对于小数加减法为什么要小数点对齐，才能更深入地理解与掌握。“计算计算，就是计一计，算一算，有多少个这样的计数单位”，算法、算理是运算能力的一体两翼。不掌握算法就无法确保实现运算能力的最低要求，但如果不知道为什么这样算，充其量只是搬弄数字的操作。计算教学中，只有沟通联系了前后的知识，才能够引导学生更好地理解算理、掌握算法，进行深度学习。

三、直观教学，激发理解算理

在教学中，由于小学生的年龄特点，“直观”发挥着不可估量的助推作用。小学生的思维处于由具体运算向形式运算过渡的阶段，如果能够在教学中用具体的、形象的事物作为学习的支持，便可以更好地将小学生的逻辑思维与抽象思维结合起来。［2］从推导过程抽象出计算法则，并学会在生活实践中运用，从而实现“学习—理解—运用—发展”的教学目标。

例如，在教学《分数乘分数》一课时，出示例题：

花园里有一块空地，王大伯准备用它的1/2 做花圃，他打算在花圃里种菊花，这是他设计的规划图，出示图1：

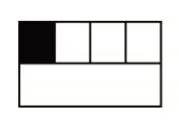
图1

图2

教师提问：“从图1 中，你能看出他准备种菊花的面积占整个空地的几分之几呢？你是怎样知道的？”（生答）“如果是按图2 规划图，种菊花的面积占整个空地的几分之几呢？怎么列式？”（生答）教师追问：“为什么用乘法？”并请学生在课堂本上列式计算。随后再让学生尝试计算出2/3×1/5 和2/3×3/5 的积，并要求学生试着画图来表示。学生有了前面直观图的经验，很快地画出直观图，并写出结果。教师引导学生思考：“每个算式表示什么意义，结果又表示什么？”在此基础上，引导学生观察四道算式中，因数与积之间的关系，你认为分数乘分数可以怎样计算？（生交流后回答）为什么要分子乘分子的积作分子，分母乘分母的积作分母呢？此时，教师以1/2×3/4 为例，利用直观图，回顾3/8 的由来：

通过直观图让学生看到，两个分数相乘，分母相乘实际是算：分了再分，一共分了多少份，分子相乘实际是取了再取，是最终取了多少份。

在整个教学过程中，直观图对于算理以及算法的形成都起着重要的作用，学生经历观察、对比、尝试画图的过程，验证得出分数乘分数的算法，更深度理解算理，培养观察能力、理解能力、推理能力、表达能力等综合能力。

四、巧设对比，促进优化算法

数学知识具有较强的系统性和逻辑性。计算教学看似简单，但是要学生知道计算的道理，知晓计算的来龙去脉，则需要教师精心设计教学方案。在计算中渗透对比思想，能够降低学生的学习难度。在对比中，对于多样的计算方法进行优化，加深学生对算理和算法的理解，同时有利于强化认知知识之间的联系。因此，对于算理中的易错点和难点，教师要给予充分的学生可以比较的素材引导，让他们从多角度进行对比，从而真正理解计算的内涵。［3］例如，在教学《异分母分数加减法》一课时，引导学生运用已有的知识经验，尝试解决1/2+1/4 的结果。学生汇报、交流各自不同的算法。（1）把1/2+1/4 分别化成小数，0.5+0.25=0.75；（2）转化成同分母分数，1/2+1/4=2/4+1/4=3/4。教师提问：“你是用什么方法计算的？为什么要通分？”（3）画图。让学生利用图形帮助理解，并比较上面的三种计算方法，哪种方法比较好，为什么？从而算法优化，突出用通分这种方法具有普遍性、最简单。掌握算法与探究算理是相辅相成的，教师要善于通过对比教学法，让学生充分体验由直观算理到抽象算法的过渡和演变过程。同时，要做到多样性和优化性的统一，从而实现对算理的深层理解和对算法的切实把握。

计算能力，不仅是教会学生会做计算题，更是运算技能和逻辑思维能力的一种独特的结合。“教会”学生计算很容易，但是要让学生深刻理解算理，并在课堂中培养学生各种能力，则需要教师深入研究计算教学，把计算教学和课程标准提出的生活情境、情感态度结合起来，使得计算教学变得生动活泼，扎实有效。