任意角三分法

聂登科

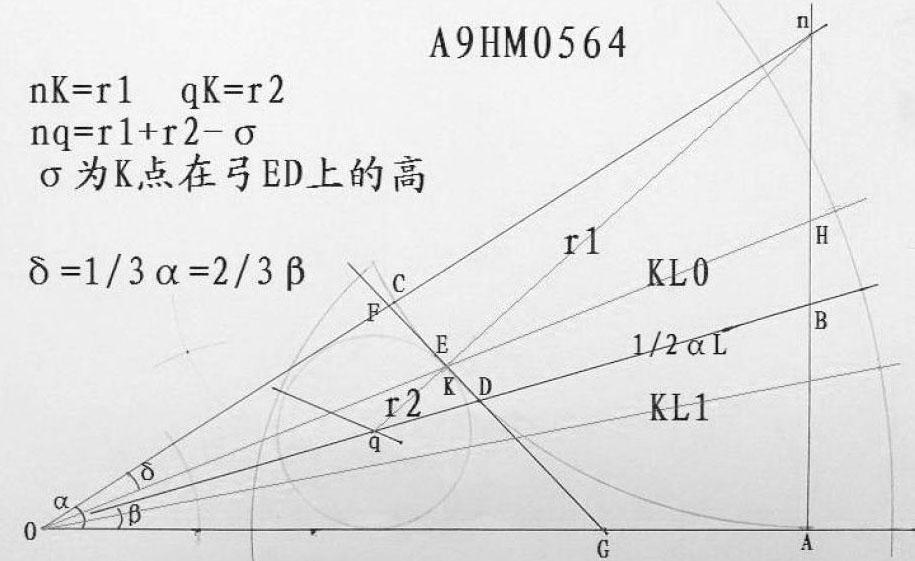
如图所示，给定任意角α，顶点为O。若角度过大过小或位置不佳等，可通过双倍缩放或旋转，完成作业后恢复即可。

在任意一边取任意一点A，并向另一边作垂线，交点n。

平分角α，平分线交nA线B点。

以nA的长度为半径r1，从A点出发，向角的另一边作弧，交C点，交平分线上D点。

取弧CD的中点E，经过E、D两点作直线交两边，分别为F、G。在△FOG中，作内切圆，得半径r2，圆心为p。

以n为圆心，r1+r2为半径，画弧再交OB线为q。

再以q为圆心，作圆相切于弧ED。切点K即为三分点！

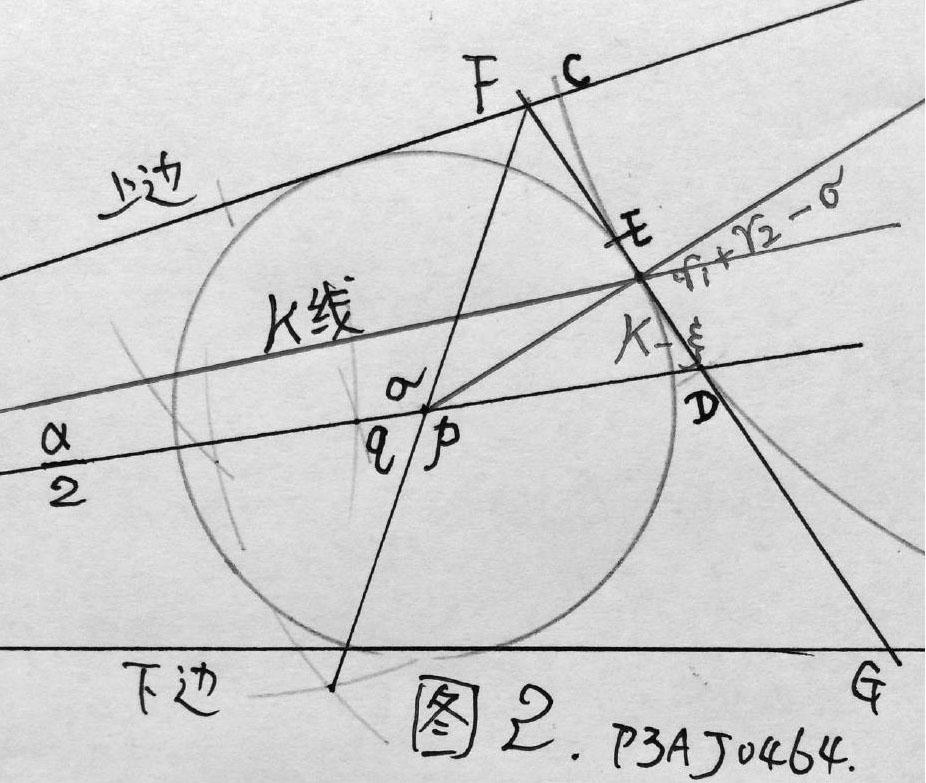
实际画图中，pq两点难以区分，两点间距是个无穷小量。理論上，前p心圆相切于弦ED，而非弧ED。后者才是K点！为纪念吾的出生地，本人命名它为K点（柯点）。

连接OK两点，即得三分线，交于H。

说明：为图面清晰，省略了部分作图线。图中未标记点、线、弧，为辅助作图和或检测之用。

如图，按r1+r2作圆，退切至弧ED后，出现了该圆周超出了α的上下两边，并非真正的内切圆了。必须修减一个微量σ，σ为K点到弦ED的距离。而且是无休止修正，致使内切圆圆心沿着α的角平分线，在p、q两点间q-σ段内，作无休止摆动，摆幅越来越小，直至无穷。同样造成K点在D点方向与ξ之间作无休止摆动，摆幅越来越小，直至无穷。用1/3的小数表述，是一个小数点无穷位后的一个3而已。事实上当人们将两颗心相连接时，K点已经确定，就是经过了无穷次修正的，无论作图水平的高低，还是画图工具仪器的优劣，理论上它就是K点无疑。

随着α角度的变化，σ和ξ的值也随之不同。恕此不细述！

本三分法通用于任意角，通过钝角锐化，旋转缩放至最合适（10-45度）角域，五步（简称A、B、弧、圆、K）即刻完成。准确简捷！

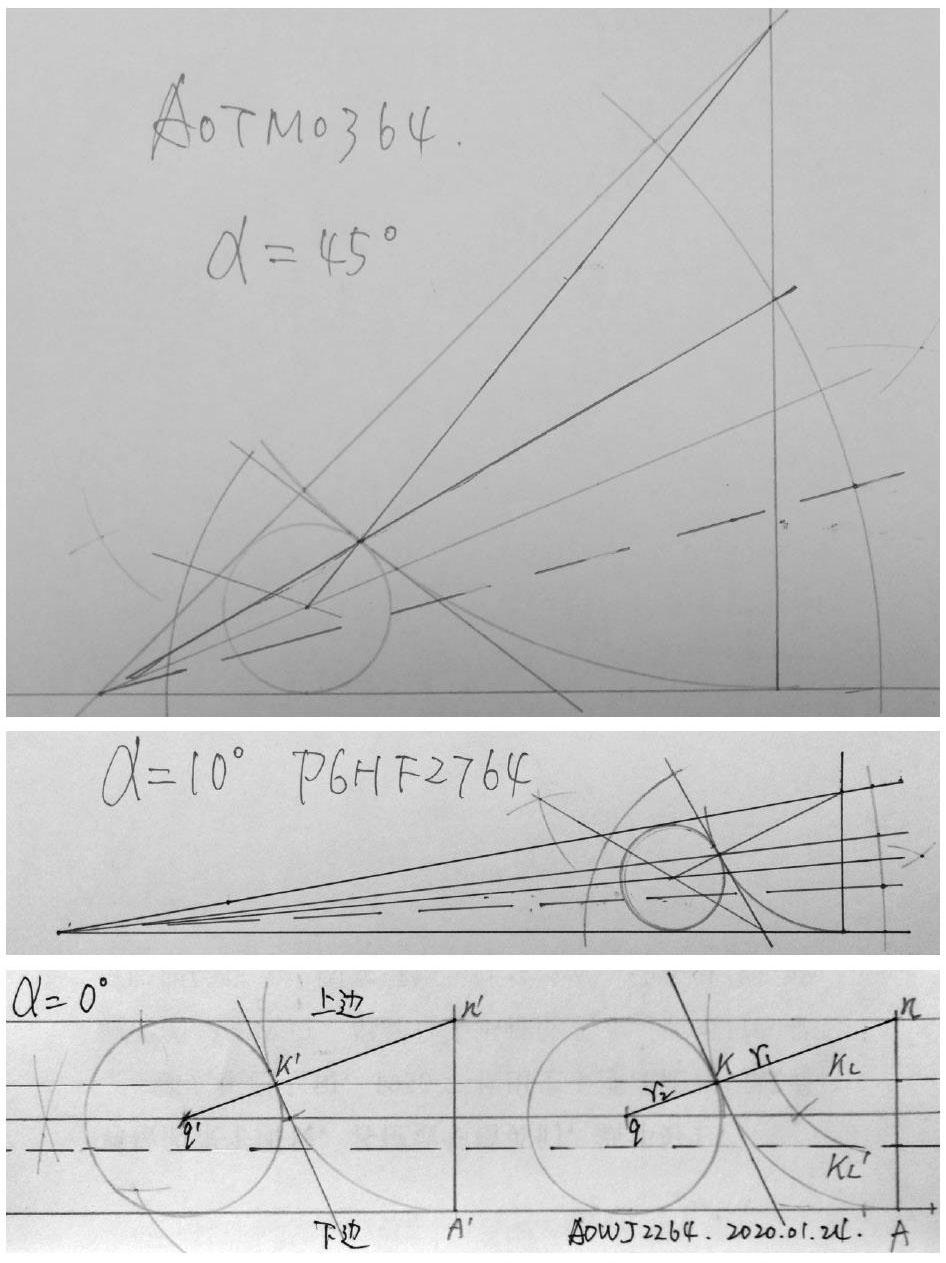
α角度越大，σ越小;α角度越小，σ越大。α角度过大，内切圆被压缩进角尖，难以准确画作内切圆，故须调整至合适的角域内操作，完成后调回。

当α=0°时，上下两边就成了两条平行线。三分法依然成立，而且由此衍生出，该三分法可三等分任意两条平行线间距。

如图，以远离顶点的小角度α角，依法画作，所有的K点均在K线上。

姑且称之为，弧圆切点法。

依法所作三分线，用几何定理，三角公式皆可证明它的存在，证明该三分法科学。

角三分线就像平分线一样，客观存在，只不过之前没有被发现而已。

由于本人没有专业的制图工具，且勉强在只能放置一张A4纸的桌面上操作，误差较大。