镜头成像畸变的MTF像高测试法研究

于西龙，龚钱冰，周 骅，杜竹青

（上海市质量监督检验技术研究院，上海 201114）

引 言

成像畸变是镜头的一种基本不良属性，是镜头品质的一项重要性能指标，每款镜头都要进行畸变测试。按畸变形态分类，畸变可分为桶形畸变和枕形畸变两种。按畸变产生原因分类，畸变可分内部畸变和外部畸变，其中：内部畸变是由于成像系统本身的构造原因而引起的，外部畸变则是因为投影方式的几何因素而导致的[1]。镜头畸变属于内部畸变，镜头产生的畸变包括径向畸变、离心畸变和薄棱镜畸变。对于常规成像系统而言，径向畸变已足够描述非线性畸变。在采用非线性优化算法进行镜头检测评价时，如果引入的非线性参数过多（如离心畸变参数和薄棱镜畸变参数），不仅提高不了检测精度，反而会导致方程解产生不稳定[2]。但对于精密机器视觉测量来说，由于是采用显微镜放大了物体的成像，小孔成像模型的无穷远视场或大伸缩比假设已经不复存在，此时，如果再采用小孔成像模型假设并忽略成像镜头的离心畸变和薄棱镜畸变，则会导致测量精度的大幅下降。

采用光学传递函数评价光学系统的成像质量，就是把物体看作由各种频率组成，也就是把物体的光场分布函数展开成傅里叶级数（物函数为周期函数）或傅里叶积分（物函数为非周期函数）的形式[3]。光学系统可以看成是线性不变的空间频率滤波器，物体经光学系统成像，可视为物体图像经光学系统传递后，其传递效果是频率不变，但对比度下降，相位要发生推移，并在某一频率处截止，即对比度为零[4]。这种对比度的降低和相位推移是随频率的不同而不同，其函数关系称之为光学传递函数。在现代光学领域，光学传递函数的方法已经普遍地应用于光学自动控制设计、光学成像系统设计的评价以及光学镜头质量的检测等方面。在评价摄影镜头成像质量方面，光学传递函数的评价方法是目前公认的最全面、最客观、最科学、最严格、最完善的方法。通过光学传递函数获得目标像高计算成像畸变的方法，能够准确地反映广角镜头成像畸变，弥补传统标板拍摄测试广角镜头成像畸变不准确、复现性差的问题，同时，采用基于MTF测试成像畸变的方法易实现自动化，可以有效减少人为因素导致的不确定度[5]。

1 理论分析

1.1 MTF 原理方法分析

光学调制传递函数（MTF）能够客观地表述光学系统的成像质量，可以直接从透镜的设计数据中计算得到[6]。利用这个方法从事光学系统设计的工作人员就可以预知光学系统的性能，同时制造厂商也可以将所生产透镜的图像质量与事先的设计效果对比，从而对产品生产线进行很好地控制。MTF为相对像对比度与相对目标对比度的比值，可以表述为MTF = Relative Image Contrast/Relative Object Contrast。在理论上，可以利用公式以较高的精度计算透镜的空间截止频率Rc和光学传递函数OTF。截止频率Rc 可表示为

式中：D为有效通光口径；R为出瞳中心到理想像点的距离（可以粗略地用焦距代替）；λ为设计使用的波长；F为视场光阑直径。透镜的光学传递函数（OTF）可表示为

式中 x 为相位传递函数（PTF），或为相位位置空间频率函数[7]。光学传递函数实际上是一个复合变换的空间频率，它的模为模传递函数，相位为相位传递函数。如果把相位传递函数表达为频率的线性表达式，那么光学传递函数可表示为像的一个简略的线性置换，就可用于描述像差，进而计算得到成像系统的几何畸变[8]。

当目标物（照明目标或十字线）与光学系统同时观察时，像会由于像差和衍射效应的原因稍微退化，此外，实物透镜也不可能完全与设计数据一致。生产误差、光机件中的装配和校准误差三个因素会大大降低光学系统的成像性能，在图像上表现为原来物体被强光照射的部分和很暗或存有阴影的部分将不会同原物那样呈现特亮与特暗的明显亮度差别。通常目标物以空间频率（每毫米内的亮、暗区域数）和对比度（图像区亮暗条纹间的亮度差别）来定义[9]。将调制传递函数在空间频率的零点进行规一化处理，目标像（十字线）亮度就会按照空间频率函数以正弦曲线变化，水平和竖直两坐标轴的空间频率值决定正弦曲线的位置或相位变化[10]。

将透镜与光学系统同时进行研究，由于像差和衍射效应的原因，会使被测图像产生失真，精确的调配和光学元件误差的校正，会减少图像失真现象的发生。在图像上，原来物体被强光照射的部分和很暗或存有阴影的部分，将不会如原物那样呈现特亮与特暗的明显亮度区别。样品差异或调制可定义为

式中：Im为重复结构显示的最大光强；In为在同一物体上发现的最小光强。

对于较低的空间频率，调制传递函数接近于1（100%）。通常，MTF曲线随空间频率的增加而下滑，空间频率越高对应的对比度值越低，如图1所示[11]。随着空间频率的增加，MTF曲线逐渐下滑直到零点，此零点被称为待测光学系统的分辨率极限或截止频率，如图2所示。当对比度值为零时，图像变得有少许均衡的灰色，同时也不再随空间频率的增加而变化。

光学调制传递函数的变化不仅与空间频率有关，而且还与视场区域的位置有关。沿光学系统对称轴进行的MTF测量称为在轴测量。为了形象地刻画光学系统的成像性能，MTF必须在视场区域的不同位置进行测量，在视场区域的不同位置进行的MTF测量称为离轴测量。为了完成MTF离轴测量，目标物需在视场区域内理想位置上移动且探测器应在相应的像位置。MTF测量只能在单一波长或覆盖波长有限波段的光谱范围内完成，测量结果由多色的MTF数值曲线中的单一色线得出。通常光学调制传递函数用于一维模式下，通过像面计算截面的方位。当狭缝或刀口延长部分顺沿于参考轴方向时，物方下的方位称为弧矢方位；当狭缝或刀口延长部分垂直于参考轴时，物方下的方位称为子午方位[12]。

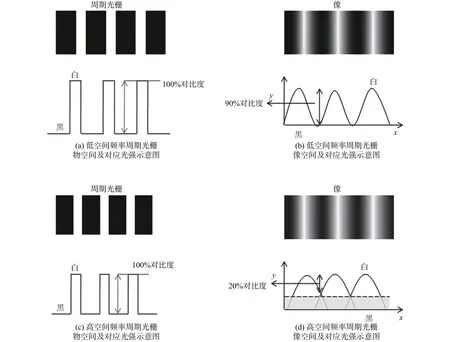
图1 透镜系统 MTF 原理图Fig. 1 MTF of camera system

图2 物像空间频率响应图Fig. 2 SFR of camera system

实际透镜的MTF值开始于1的位置，并随着空间频率的不断增大而逐渐衰减。由透镜引起的图像模糊导致振幅随着空间频率的增加而减少，性能优良的成像系统曲线（如图2中的点划线）要好于那些质量较低产品的曲线（图2中的实线），并且能在更高的空间频率下有更有效的传递对比度[13]。图3为物像光的调制变化，左侧的正弦波表示物方光，右侧波表示经被测系统后的像方光。

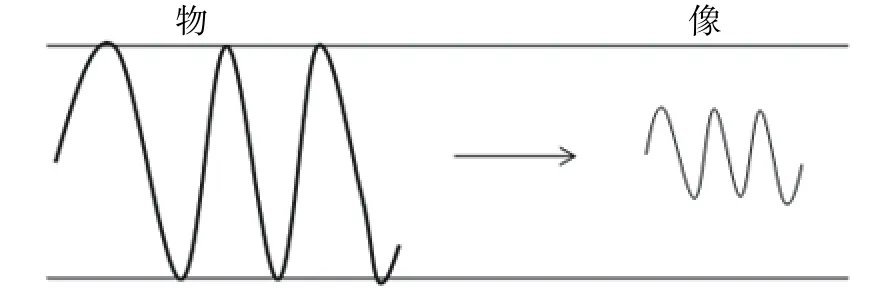
图3 物像调制变化示意图Fig. 3 Image modulation variation

通常用线扩散函数（LSF）来描述调制传递函数。同时线扩散函数还可用于描述一元目标物（分划板）的尺寸和强度分布。调制传递函数（MTF）是由线扩散函数经傅里叶变换得到，与空间频率整个范围内正弦波的积分和相等，如图4（a）所示。由于MTF的傅里叶特性，它只能用于处理正弦频率[14]。傅里叶数学分析使得任何描绘目标物（分划板）剖面强度的函数都可以用来分析不同频率的正弦波和不同相位关系。根据MTF在图像系统的特性，首先需要将目标物经傅里叶变换转化为它的频谱，然后与系统MTF相乘，最后再经逆变换得到经过修正的像轮廓图，如图4（b）所示。

图4 MTF 与 LSF 的傅里叶函数关系Fig. 4 Fourier relationship MTF and LSF

1.2 畸变测量原理

畸变是主光线的像差，由于球差的影响，不同视场的主光线通过光学系统后与高斯像面的交点高度不等于理想像高，其差别就是系统的畸变。通常用（a，b）表示图像点的实际坐标值，εa与εb是水平和垂直两个方向上的非线性畸变值，它们满足如下关系式：

式中：μ1、μ2、η1、η2、λ1、λ2为线性畸变系数。式（5）的第一部分μa（a2+b2）称为径向畸变，第二部分η（3a2+b2）+2ηab称为离心畸变，第三部分λ（a2+b2）称为薄棱镜畸变。本文采用的计算畸变的方法为计算实测有效焦距f和理想焦距f0的相对畸变δr，其表达式为

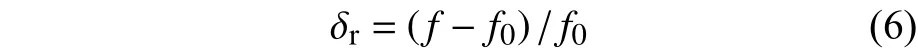
f可以通过测量近轴像高的变化量和视场角的变化量来获得，即

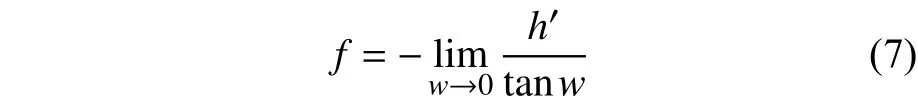
式中：h′为像高；w为物方视场角。有效焦距的测量原理如图5所示，首先将像方导轨移动到正方向，即像高向正方向偏离某一位置（像移），然后物方视场角移动到w1，探测器扫描像的光强信号，得到线扩散函数，给定线扩散函数的中心位置。将像移动到中心视场（0°），再将物方视场角移动到0°，扫描线扩散函数。像方导轨移动到负方向，即像高向负方向偏离某一位置（像移）。物方视场角移动到w3，扫描线扩散函数。有效焦距（EFL）的计算公式如下：

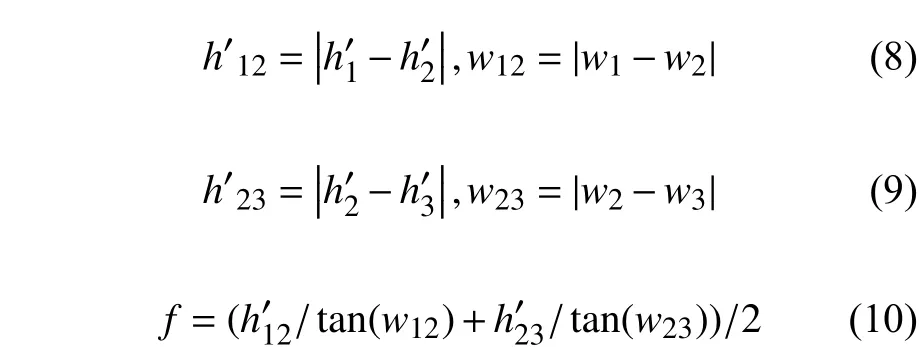
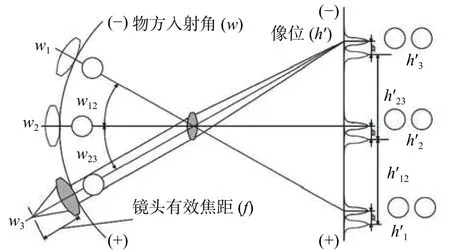
图5 EFL 测试原理图Fig. 5 The principle of EFL measurement

图6 为畸变测试原理图，首先要测量轴上的EFL，将物方视场角移动到轴上位置，通过扫描LSF获得在此位置的像高h1，根据焦距公式计算此位置的EFL值。再将物方视场角移动到离轴位置，扫描计算过程同前所述。当完成最大视场角位置的测量后，物方视场角移动到反方向离轴的位置。测量过程同前，后续以此类推，直到测完最大视场角位置。

2 测试过程

本文分别对16款不同型号的照相机可更换镜头进行了标板（见图7）拍摄法畸变测试和MTF方法畸变测试，并对测试结果进行了比较分析。测试镜头样品中有9台为变焦距镜头，7台为定焦距镜头，焦距从5 mm到600 mm不等，均为市场主流品牌，测试环境符合国家照相镜头检测标准。

图6 畸变测试原理图Fig. 6 The principle of distortion measurement

图7 标准畸变测试图Fig. 7 Distortion-checker chart

标板拍摄法的畸变测试过程如下：

a）被检镜头光轴与畸变测试标板垂直，并使畸变测试标板充满像面（标板与镜头物方主点的距离为镜头等效焦距的30倍）。用被检镜头（变焦距镜头分别用长焦端和短焦端）对畸变测试标板进行正确拍摄。

b）将所拍摄的畸变测试标板图像输入计算机，用图像处理软件判读在像面对角线上0.5y′和0.8y′处的像素数（以线宽的外侧度量）。其中y'表示有效像场半径（像高），等于像面对角线长度的1/2。测试结果见表1，表中δ1、δ2、δ3为畸变的三次测试结果。

MTF方法畸变测试过程如下：

试验仪器为德国TRIOPTICS公司的光学传递函数测量仪ImageMaster®Universal，如图8所示。在暗室环境下，将待检镜头安装在光学

传递函数测量仪正确位置，通过反复移动光学传感器，找到不同焦距镜头的最佳像点，测量有效视场角内各物方视场角对应的MTF值，进而获得f和f0，然后通过式（6）计算得到各对应物方视场角的畸变。为了便于和标板拍摄法畸变测试结果相比较，同样选取0.5y′和0.8y′处的畸变值，各镜头采用MTF方法测得的畸变值见表2。

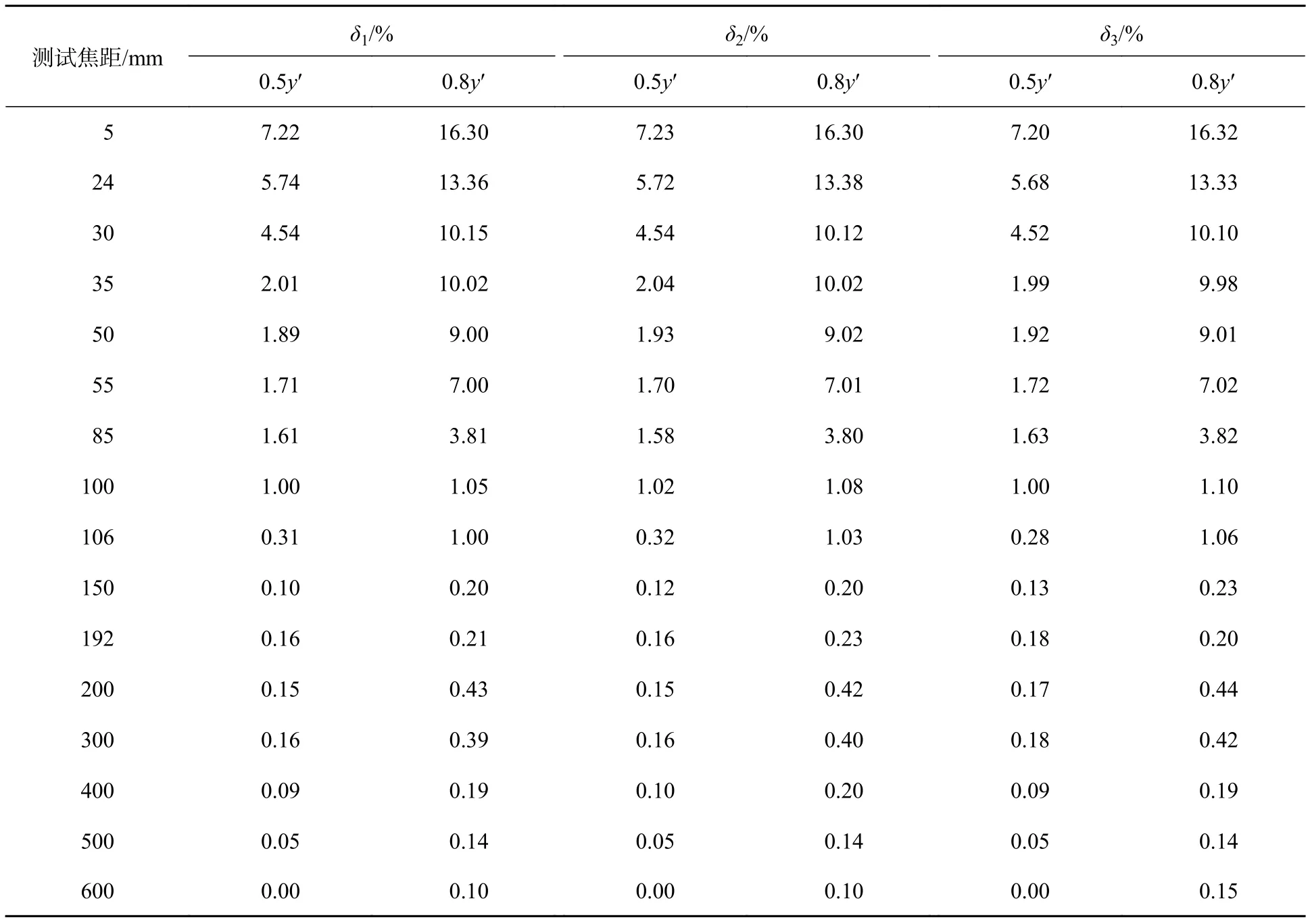
表1 标版拍摄法畸变测试结果Tab. 1 Distortion result of standard pattern image test

图8 光学传递函数测量仪（型号：ImageMaster® Universal）Fig. 8 MTF measurement apparatus（Model: ImageMaster® Universal）

为进一步验证两种畸变测试方法的准确性，对7款定焦距镜头分别进行畸变检测，并将标板拍摄法和MTF方法测得的0.5y′和0.8y′处的畸变值与该镜头出厂前测得的实际畸变值进行比较，结果见表3。

表2 MTF 方法畸变测试结果Tab. 2 Distortion result of MTF measurement

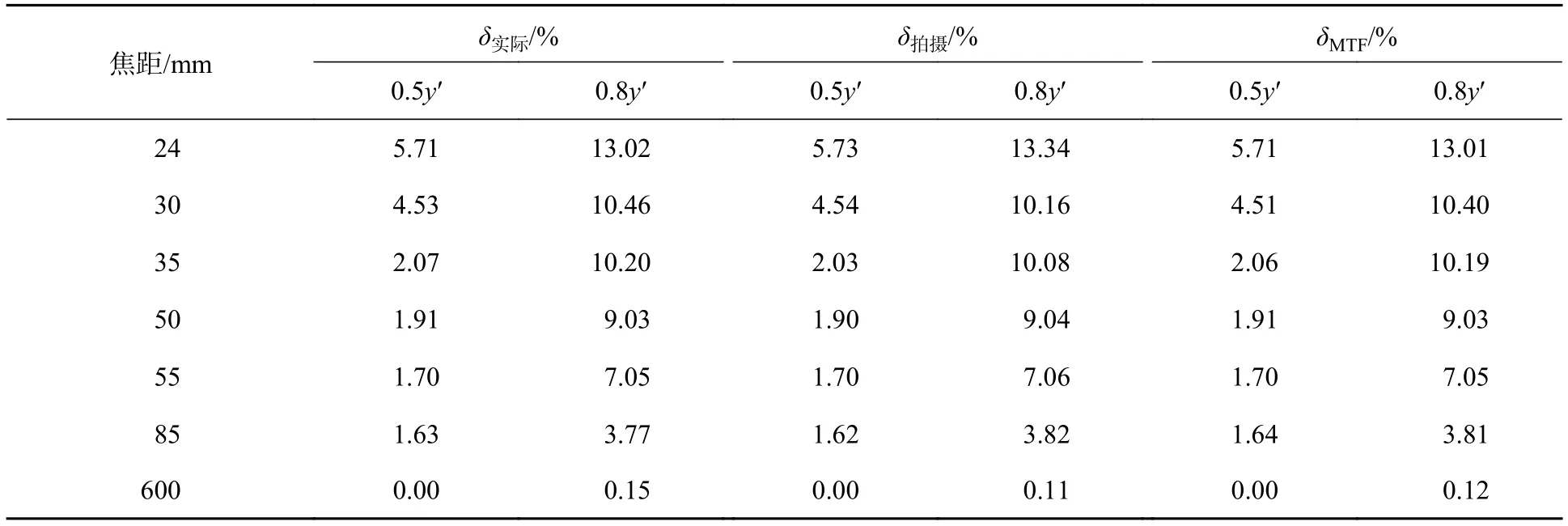
表3 畸变测试结果比对Tab. 3 Comparison of distortion test results

3 结 论

传统标板拍摄法畸变测试结果表明，同一镜头在相同测试环境条件下，重复的测试结果之间存在偏差，最大偏差为2.9%，平均偏差为2.0%，偏差较大。而采用MTF方法进行畸变测试，测试结果之间最大偏差为1.1%，平均偏差为0.8%，特别是对于焦距在150 mm以上的中长焦距镜头的畸变，测试结果几乎没有偏差。由此可见，采用MTF方法进行镜头畸变测试的重复性比采用传统标板拍摄法更好。将两种方法测试结果与畸变实际值进行比对，两种方法测试误差均在国家标准要求范围以内，但MTF方法更接近实际值。

在相同环境条件下，用两种方法对同一款镜头进行畸变测试，并对结果进行比较。经计算，可得到两种方法的最大测试偏差为4.0%，偏差较大，经对测量数据进一步分析，可以得到：两种方法对100 mm焦距以上的镜头畸变测试结果的最大偏差为2.0%；两种方法对150 mm焦距以上镜头畸变测试结果的最大偏差为0.1%。由此可见，两种方法的测试结果差异主要集中在短焦镜头，究其原因，是采用传统标板拍摄法进行畸变测试时，短焦镜头由于畸变偏大而导致边缘形变严重，每次取景时拍摄位置都会有差异，这种位置的差异会造成拍出来的图像不一致，进而图像分析软件读出来的畸变数据会有差异。采用同样的方法进行畸变测试，短焦镜头的测试结果比长焦镜头的测试结果重复性更差也印证了这一点。所以，采用MTF方法进行镜头畸变测试本身不会造成测试结果偏差，且理论上比传统标板拍摄法测试的镜头焦距范围还要广。