回转式贴标机取标工位凸轮曲线改进设计*

李全来

（北京工商大学材料与机械工程学院，北京100048）

回转式贴标机取标工位凸轮曲线改进设计*

李全来

（北京工商大学材料与机械工程学院，北京100048）

回转式贴标机取标工位凸轮曲线的合理设计是保证贴标质量的关键环节之一。在以取标板和标签无相对滑动为条件建立的滚柱运动轨迹方程基础上，选用组合摆线运动规律设计了新型凸轮曲线。结果表明该凸轮曲线能使滚柱位移误差和取标工位所占用的凸轮转角均较小；以取标板摆动过程中切点的最小纵坐标值作为标盒相对转盘回转中心的安装距离，可以使取标板与标签保持相切，从而为回转式贴标机提供了一种新型取标工位凸轮曲线。

回转式贴标机；取标装置；取标工位；凸轮曲线

0　引言

回转式贴标机是用黏结剂将标签贴于圆柱形包装件指定位置上的一种贴标机械［1］，具有工作效率高、操作方便、性能稳定的优点，在饮料、日化、食品、医疗等行业中应用非常广泛。近年来，随着产品生产规模的不断扩大，人们对贴标机的需求量也越来越大，对贴标速度、贴标质量提出了更高的要求。

取标装置是回转式贴标机的核心部件之一，是影响贴标速度和贴标质量的重要因素［2］。目前取标装置主要分为胶黏式取标装置、真空转鼓式取标装置和摩擦式取标装置等［3］。胶黏式取标装置是啤酒贴标机的重要机构。它主要由取标板、转盘、槽凸轮、滚柱、扇形齿轮等组成［2］。工作过程中取标装置在凸轮-齿轮组合机构的控制下依次经历上胶、取标和夹标工位，将涂有胶水的标签输送至贴标工位。上胶指用胶辊为取标板均匀地涂上胶水的过程；取标指粘有胶水的取标板转至标盒时从标盒中粘出一张标签的过程；夹标指夹标转鼓从取标板上揭下已涂胶的标签并转至贴标工位的过程。取标工位是取标装置工作过程的一个重要环节，是保证正常夹标的前提。近年来国内外研究者围绕取标工位取标板的结构和运动规律展开了许多研究。陈金元［4］认为取标过程中取标板应在标签上做匀速滚动，用匀速运动规律设计了取标工位凸轮曲线。肖仲湘［2］指出取标时取标板应在标签上做纯滚动，而且取标板摆动过程形成的包络面应为一平面，该平面与标签所在平面贴合，建立了以转盘转角为自变量的取标板摆角计算方程。兰云志［5］分析表明当取标板在标签上做纯滚动时，取标板自转中心的理论运动轨迹应为摆线，而实际运动轨迹为圆周，计算了取标板自转中心理论和实际运动轨迹之间的误差。张俊玲［6］分析了取标过程中取标板和标签的相对滑动量和法向位移量，以无相对滑动为条件计算了取标板曲率半径和偏心距。林丽明［7］以取标过程中取标板上切点相对静止为条件，优化了取标板曲率半径和公转半径。

取标过程中取标装置通过凸轮机构控制扇形齿轮摆动，进而拨动取标板齿轮转动，带动取标板运动，从而使取标板从标盒中粘取标签。实现取标板取标动作的关键是取标工位凸轮曲线设计。本文在以取标板和标签无相对滑动为条件建立的滚柱运动方程基础上，设计取标工位凸轮曲线，计算滚柱实际位移和取标板摆动过程形成的包络线，分析滚柱位移误差和取标板与标签的法向相对位移量，为回转式贴标机取标工位凸轮曲线的改进设计提供依据。

1　取标工位滚柱运动轨迹分析

理论上取标过程中取标板与标签应既无相对滑动又无法向相对位移［2］。研究表明上述两个条件无法同时满足［2，6，8］。当取标板与标签有相对滑动时容易导致粘在取标板上的标签出现褶皱、不平整；当取标板与标签有法向相对位移时，取标板与标签不能保持相切。为保证有效取标，通常以取标板与标签无相对滑动为设计条件，再通过安装弹簧式标盒消除取标板与标签的法向相对位移的影响，保证整个取标过程中取标板与标签保持接触［2，5-6］。

取标工位滚柱运动分析如图1所示。转盘绕中心Oo匀速转动。取标板自转中心为C，曲率中心为Ob，曲率半径为Rb。取标板在自转的同时绕Oo公转，公转半径为R0。取标板的偏心距为e，D为取标板上弧中点。标签M1M2的长度为L，中点为N。转盘转角α为OoC与y轴的夹角，取标板的摆角β为OoC与ObC之间的夹角，取标板的自转角ψ为ObC与y轴的夹角。扇形齿轮自转中心为OS，同时绕Oo公转，公转半径为R0。扇形齿轮的转角为γ，其上装有滚柱E。滚柱的另一端安装在槽凸轮中。

图1　取标工位滚柱运动分析

当转盘逆时针方向转动时，取标板顺时针方向摆动，扇形齿轮逆时针方向转动，对应凸轮的降程段。当B1与M1接触时开始取标，当B2与M2接触时完成取标，取标板弧长与标签长度相等。取标板的摆动过程关于y轴为对称［2，4］。当D与N接触时α=ψ=β=γ=0，切点D的坐标为（0，R0+Rb-e）。

当转盘转角为α时，B与M相切。取标板摆过的弧长应等于它粘取到的标签的长度，即SB1B=M1M，则［2］：

对于给定的α通过式（4）就可以计算出相应的取标板摆角β。

切点B的坐标为［2］（β-α）Rb，R0cosα+Rbecos（β-α）。

则取标板初始摆角为：

在ΔOoCOs中［3］，O0C2=O0Os2+OsC2-2× O0Os×OsC×cos∠OoOsC（6）

则∠O0OsC=arccos（7）

∠O0OsE=∠O0OsC+γ=∠O0OsC+（8）

在ΔOoEOs中，O0E=+OsE2-2×OoOs×OsE×cos∠OoOsE（9）

E的运动轨迹即为取标工位滚柱的理论运动轨迹。

2　取标工位凸轮曲线改进设计

经过试算，当取标过程中凸轮机构用摆线运动规律时滚柱的实际位移与理论运动轨迹之间的误差较小。但是在摆线运动的始、末段，滚柱的运动速度很小，这导致中间段类加速度很大，易产生剧烈的冲击［9］。为了减小中间段类加速的幅值，需要在摆线运动的始、末段用其他类型的运动规律构成组合运动规律。在选用组合运动规律时应使整个取标工位所占用的中心角尽量小，这将便于下一步取标和夹标工位凸轮曲线的优化设计。组合摆线运动的始、末段所占凸轮转角仅为整个运动过程中凸轮转角的1/4［9］，因而选用组合摆线运动规律。即滚柱的运动分为三段，摆线运动加速段、中间摆线运动段和摆线运动减速段。

设h为滚柱的总工作行程，对应的凸轮总转角为φ，摆线运动加速段、减速段和中间段所占的凸轮转角分别为ϕ1、ϕ2和ϕ3，则ϕ1=ϕ2=0.125φ，ϕ3=φ-ϕ1-ϕ2=0.75φ。

而中间摆线段凸轮转角即为取标过程中转盘的转角，所以ϕ3=2α0。由此可计算出取标工位凸轮总转角φ==3.667α0。

若对凸轮转角归一化，则x1==0.125， x2=1-=0.875，x3=0.75。

摆线运动加速段、减速段和中间段所占的工作行程分别为h1、h2和h3，则总工作行程为：

其中，O0Emax和O0Emin分别为取标过程中O0E的最大值和最小值。

当凸轮基圆半径为rb，滚柱半径为rT时，滚柱位移为 s=O0E-rb-rT，归一化的位移 y为y=s/h（0≤y≤1）。

根据降程期组合摆线运动规律中间段工作行程计算公式［9］可得：

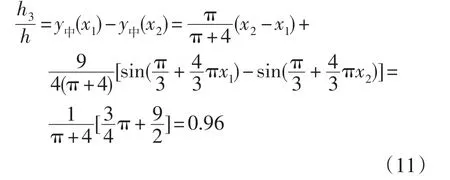
则凸轮总工作行程为：

根据降程期组合摆线运动规律可计算出任意归一化凸轮转角x对应的滚柱归一化位移y，再通过s=yh便可求出摆线运动加速段、减速段和中间段的滚柱实际位移。

3　取标工位凸轮曲线设计实例

回转式贴标机胶黏式取标装置的参数如表1所示［4，10］，编写MATLAB程序设计取标工位凸轮曲线。

表1　回转式贴标机胶黏式取标装置参数

由式（4）可得α0=22.54°，则ϕ3=45.08°，φ=60.11°，ϕ1=ϕ2=7.51°。即摆线运动加速段凸轮转角为0≤ϕ＜7.51°；中间摆线运动段凸轮转角为7.51°≤ϕ＜52.59°；摆线运动减速段凸轮转角为52.59°＜ϕ≤60.11°。

由式（12）可得凸轮总行程为：

中间摆线运动段凸轮转角与滚柱位移列于表2。s为滚柱理论位移，s′为滚柱实际位移，Δs为滚柱位移误差。滚柱平均位移误差为0.113 mm，最大位移误差2.217 mm。

表2　中间摆线运动段凸轮转角与滚柱位移

摆线运动加速段的位移、类速度和类加速度方程：

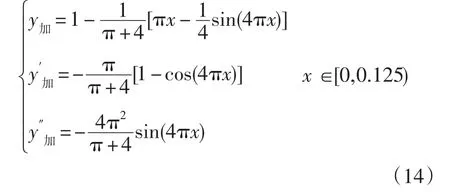
中间摆线运动段位移、类速度和类加速度方程：

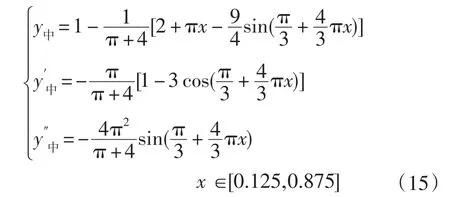
减速段的位移、类速度和类加速度方程：

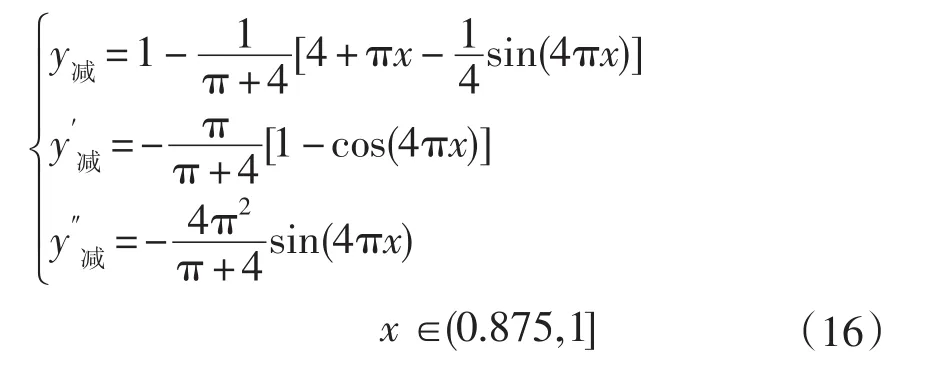
取标工位滚柱运动规律如图2所示。

图2　取标工位滚柱运动规律

根据凸轮转角及相应的滚柱位移用MATLAB［11］绘出取标工位凸轮轮廓曲线，如图3所示。为保证凸轮传动有良好的力学性能，需要校核取标工位凸轮压力角。当许用压力角为30°时，查诺模图［9］可得出的许用值为1.0。采用组合摆线运动规律时==0.54＜1.0，说明凸轮传动过程中最大压力角小于许用压力角，可以保证传动时凸轮机构受力良好，凸轮轮廓线设计合理。

在取标过程中保证取标板与标签无相对滑动时，取标板摆动形成的理论包络线为a，直线为b为标签所在位置，如图4所示。a与b不重合说明取标板与标签之间有法向相对位移，这与肖仲湘［2］、陈金元［4］的分析结论一致，即无法同时满足取标板与标签既无相对滑动又无法向相对位移。凸轮机构采用组合摆线运动规律时取标板摆动形成的包络线为c，保证了取标过程中无相对滑动。在安装弹簧式标盒时标盒与转盘回转中心间的距离可为取标板摆动过程中切点B的最小纵坐标值，即OoN=Ymin=174.119 4 mm。这能使取标过程中取标板与标签保持相切，从而消除取标板与标签法向相对位移对取标过程的影响。

图3　取标工位凸轮曲线

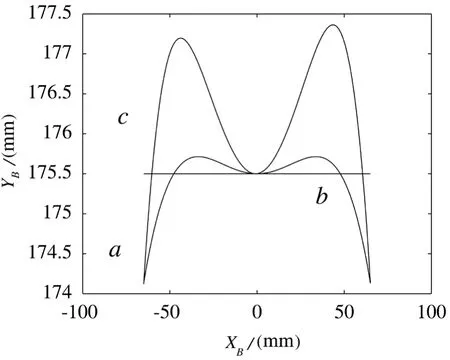
图4　取标工位取标板摆动形成的包络线

4　结论

根据回转式贴标机取标工位取标板的运动要求，在以取标板和标签无相对滑动为条件建立的滚柱运动方程基础上，用组合摆线运动规律设计了取标工位的凸轮曲线，计算了滚柱位移误差和取标板摆动形成的包络线。取标工位滚柱位移误差平均值为0.113 mm，取标工位所占用的凸轮中心角仅为60.11°。在安装标盒时用取标板摆动过程中切点的最小纵坐标值作为标盒相对转盘回转中心的安装距离可以保证取标板与标签保持相切。结果表明用组合摆线运动规律设计的凸轮曲线能有效完成取标动作，为回转式贴标机提供了一种新型凸轮曲线。

［1］金国斌，张华良.包装工艺技术与设备［M］.北京：中国轻工业出版社，2008.

［2］肖仲湘.贴标机凸轮齿轮组合机构的研究［J］.轻工机械，2000（01）：21-26.

［3］黄颖为.包装机械结构与设计［M］.北京：化学工业出版社，2007.

［4］陈金元.回转式贴标机贴标部件的运动分析及凸轮设计原理［J］.无锡轻工业学院学报，1992，11（1）：52-61.

［5］兰云志，李乐山.高速贴标机数学模型研究与参数设计［J］.轻工机械，2003（01）：33-36.

［6］张俊玲.回转式贴标机凸轮的设计与研究［D］.济南：山东大学，2006.

［7］林丽明，李定华，李允文.回转胶粘式贴标机机构的计算机辅助设计［J］.广东机械学院学报，1994（02）：20-25.

［8］张芙蓉.贴标机取标机构设计探讨［J］.轻工机械，1998（02）：21-24.

［9］侯书林，尹丽娟.机械设计基础［M］.北京：中国农业大学出版社，2013.

［10］李全来.回转式贴标机上胶工位凸轮曲线优化［J］.轻工科技，2014（12）：48-50.

［11］郭仁生.机械工程设计分析和MATLAB应用［M］.北京：机械工程出版社，2012.

Improved Design of Cam Curve in Picking Workplace of Rotary Labeling Machine

LI Quan-lai
（School of Material and Mechanical Engineering，Beijing Technology and Business University，Beijing100048，China）

Reasonable design of the cam curve in picking workplace of rotary labeling machine is one of the key links in the labeling quality assurance.Based on the roller trajectory equation，which is developed conditioned on no relative sliding between the picking-up plate and label，the cam curve is designed using combined cycloidal motion.It can be seen from the results that both roller displacement error and cam angle occupied by picking workplace are small.In order to make picking-up plate and label keep tangent，the minimum longitudinal coordinate value of tangent point during picking-up plate swing is employed as the mounting distance between label box and the turntable rotation center.It provides a novel cam curve in picking workplace for rotary labeling machine.

rotary labeling machine；picking-up device；picking workplace；cam curve

TB486

A文献标识码：1009-9492（2015）12-0057-05

10.3969/j.issn.1009-9492.2015.12.016

李全来，男，1982年生，天津人，博士，讲师。研究领域：机械设计。已发表论文10篇。

（编辑：向飞）

*北京市教育委员会科技发展计划面上项目（编号：KM201310011003，KM201510011005）

2015-11-16