基于迁移学习的VGG-16网络芯片图像分类

马 俊，张荣福，郭天茹，张喆嫣，李 卿，王 蓉，李子莹

（上海理工大学 光电信息与计算机工程学院，上海 200093）

引 言

随着半导体产业的不断发展，芯片生产工艺的要求不断提高，引线键合的质量检测已成为保证芯片质量的重要部分。通常引线键合质量检测采用图像法进行[1]，该方法利用显微镜小景深的特点，通过调节视场以及显微镜载物台的高度，完成对引线局部特征和高度信息的采集，通过对焊盘的位置、焊球的直径以及键合线弧高的检测来判别引线键合的质量。

由于芯片结构的复杂程度较高，传统的卷积神经网络模型对芯片连接丝、焊球、焊盘的分类效果较差，又因为本实验的数据集较少而且还需要对图像进行人工标注，这不仅耗时而且会影响最终的预测效果。为了解决这一个难题，本文将基于迁移学习的VGG-16网络方法应用在芯片图像的分类上，即对采集的芯片图像进行三分类，分别为芯片焊盘、芯片焊球以及连接丝图像[2-3]。迁移学习是用来解决深度学习中数据集量不足的问题，它是将已经训练好的模型参数移植到新模型中并辅助新模型完成训练。又因为大部分的数据以及任务都是相关的，所以利用迁移学习的方法，将训练好的模型参数分享到新模型中，这样不仅能够减少人工标注数据的工作，还可以减少模型的训练时间，提高模型的学习效率，充分利用以往的学习经验，有利于提高和改善传统深度学习的训练效率。

1 卷积神经网络理论

卷积神经网络主要是由卷积层、池化层和全连接层组成，通常会选取若干个卷积层和池化层交替连接在一起[4]，利用卷积层中的卷积核来提取数据的深层信息以及图像的局部特征[5]。卷积运算的目的是提取输入的不同特征，然后再将这些特征输入到下一层中。卷积层的计算公式如下：

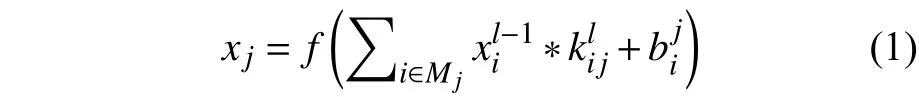
式中：*为卷积操作；Mj为特征图的集合；l为第l层的网络；k为卷积核参数；b为偏置；xj为输出；为 l层输入；f（a）为激活函数。

池化通常又叫欠采样或下采样。主要用于特征降维，减少数据和参数的数量。根据池化的规则计算出每个小区域的对应值，再将所得到的值重新排列，得到一个新的特征图[6]。池化通常分为最大池化和平均池化。最大池化是取出这个区域中的最大值作为下一层的特征，而平均池化则是计算出这个区域所有特征的平均值作为下一层的特征。本文是采用最大池化来提取区域中的最大值，并将此最大值作为下一层特征。计算方法如下：

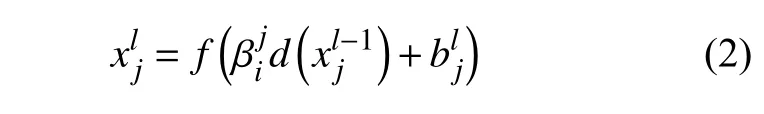
式中：d（）为池化函数；β为权重系数；b为偏置。

2 图像采集

采用50倍的显微系统[7]进行图像采集，运动机构和驱动芯片使载物台平移和升降，通过电子目镜采集一系列图像用以构成数据集。数据集包含了清晰的、模糊的、信噪比低的多种不同类型的图像，相机拍摄到的图片分辨率为1 920×1 200。在图像采集的过程中要满足以下两个方面：

（1）芯片要有不同的放置角度。为了增加样本的多样性，将采集各种不同旋转角度的图像作为数据集，这样做有利于提高深度学习的鲁棒性。

（2）图像要有不同的模糊度。为了提高网络模型的精确性，采集不同模糊度下的图像，如图1所示。

3 图像预处理

首先根据VGG-16网络的计算要求，通过下采样的方法将我们所采集到的图像的大小裁剪为224 × 224，然后对原始图像进行预处理。为了减少后期模型训练的运算量，加速模型的收敛速度，提高后续步骤的可靠性，我们需要对图像进行归一化的处理。图像归一化是对图像进行了一系列标准的处理变换，使之变换为固定标准形式，该标准图像即为归一化图像。图像归一化最常见的方法是最大最小值归一化方法，可表示如下：

图1 不同模糊度Fig. 1 Different ambiguity

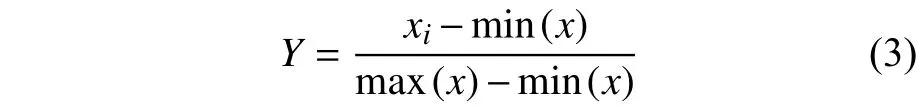
式中：xi为图像像素点值；min（x）、max（x）分别为图像像素的最小值与最大值。

4 VGG-16 network

本文采用了VGG-16网络的宏架构，如表1所示，该模型是由13个卷积层、5个最大池化层以及3个全连接层构成。利用卷积滤波器（kernel）对特征图进行卷积运算[8-10]，对ImageNet数据集输入的各种图像进行特征提取。从每个内核中取最大值的最大池化操作减少了特征映射的大小，并确保了固定的输出大小。卷积的步长和最大池化的step （filter slide的单位数）分别设置为1和2。全连接层对输出层采用soft-max函数，使模型可以做三分类预测。

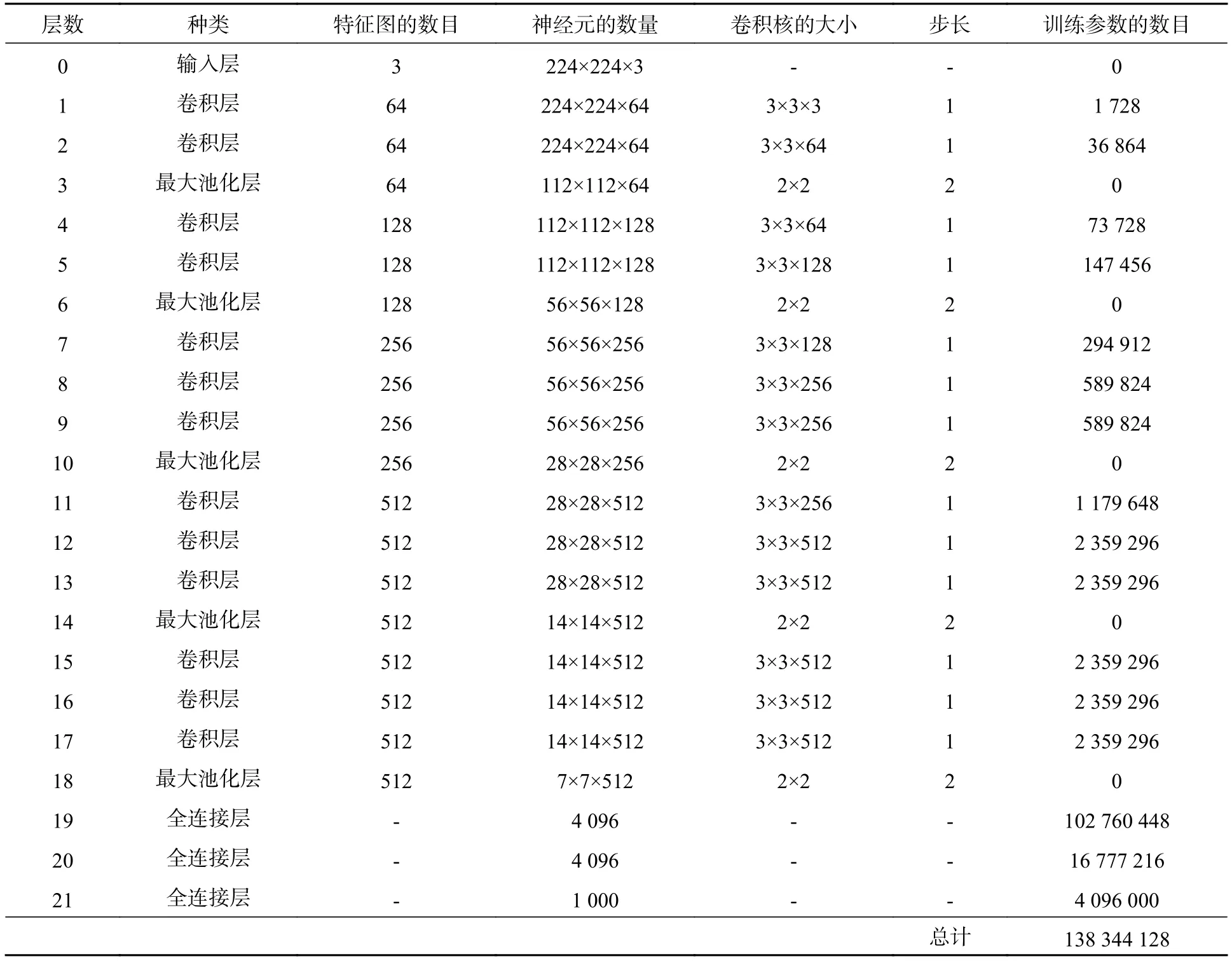
表1 VGG-16 网络结构Tab. 1 The details of architecture of VGG-16 network

VGG-16网络的输入固定尺寸为224×224×3，每个尺寸分别表示宽度、高度和信道。首先，输入层与64个3×3×3内核进行卷积，构建第1层；然后，在第 1层用 64个 3×3×64个核进行卷积；再然后，执行2×2最大池化操作生成layer 3；以此类推，直到第18层，其中产生了7×7×512个神经元；全连接层由19层至21层排列，第18层的神经元与第19层的4 096个神经元完全连接，第19层与第20层完全连接，共有4 096个神经元；最后，将第20层与第21层（输出层）完全连接，输出3个神经元，表示3个类别。本文采用绝对误差来作为模型的损失函数，其表达式如下：

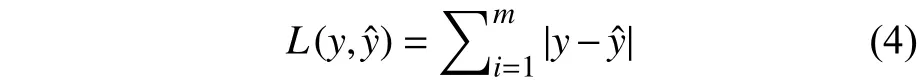
式中：L为损失函数；y为样本的标签；为模型的预测值；m为样本数量。

5 迁移学习法

针对芯片图像数据集相对较小、模型训练时间较短的特点，在数据集上对预训练的VGG -16网络进行微调以增加训练量，为此本文提出一种适应分类的迁移学习方法，如图2所示。首先对卷积（conv）层进行初始化，加载预训练权值，初始计算并存储权值，减少冗余过程，加快训练速度；然后随机初始化三层全连接（fc）层的权值，学习数据集图像与芯片图像之间的特征空间迁移；最后的一个全连接层由ImageNet的1 000个输出类调整为芯片底盘、焊接球和芯片引脚连接丝3个输出类，并将soft-max激活函数改为logsoft-max激活函数，用来提高分类的准确率，避免梯度消失；再然后，我们将所有卷积层和相应的最大池化层设定为固定的特征提取器；最后，将数据集中的图像输入到改进后的网络中，对其进行再次训练，在数据集中检测出我们所需的三分类。在再训练过程中，我们通过芯片图像的反向传播来更新预训练的权值，以达到微调卷积层效果，同时避免过拟合。

新初始化的网络是在Ubuntu 16.04操作系统上进行训练的，该操作系统使用Intel Core i7-2700K 4.6 GHz CPU、256 Gb RAM、基于pci的双AMD Filepro 512 Gb闪存和NVIDIA GTX 1080 8 Gb GPU进行培训和验证。我们使用SGD优化器，以每步1 000张图像为批次训练图层，学习率为0.001，动量为0.9，权值衰减为10-4。经过200次迭代后，由于精度和交叉熵损失都没有进一步提高，随即停止了训练。

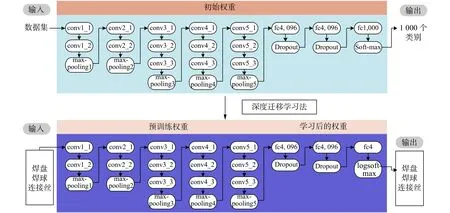
图2 迁移学习法原理图Fig. 2 Schematic of transfer learning method.

6 实验及结果

6.1 数据集的构建

在对数据集进行划分时，通常采用自助法、留出法以及交叉验证法。在测试集选取时，原则上选取的测试集要与训练集保持互斥的状态。本实验通过分层采样和等距抽样相结合的办法来获取训练集和测试集，充分保证了样本结构与总体的一致性，提高样本的代表性。

本实验所用的数据集是由芯片连接丝、焊盘以及焊球三部分构成，共2 400张图片，其中连接丝、焊盘以及焊球各800张，每张图片都通过显微镜采集获得。为了评价本文提出方法的效果，分别从数据集中选取了连接丝、焊盘和焊球各200张图像，共600张图像作为测试集，其余的图像作为训练集。利用建立的训练集对VGG-16网络上层的权值进行反向传播再训练，并使用测试集对模型进行性能评估。数据集的组成如表2所示。

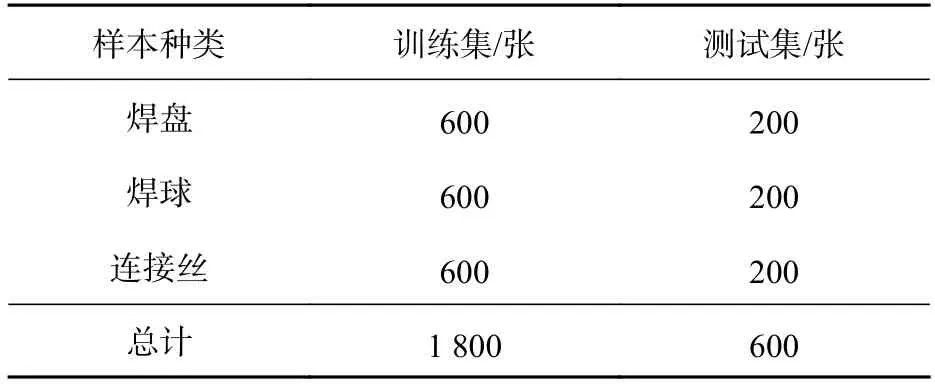
表2 图像数据集Tab. 2 Image datasets

6.2 评价指标

利用准确率、F1-Score和混淆矩阵可对实验结果进行评价。准确率就是测试集中正确分类的数量占整个测试集数量的百分比，表达式为

式中：TP表示的是将正类预测为正类数，真实为0，预测也为0；FN表示的是将正类预测为负类数，真实为0，预测为1；FP表示的是将负类预测为正类数，真实为1，预测为0；TN表示的是将负类预测为负类数，真实为1，预测也为1。F1-Score指标综合了精确率（Precision）和召回率（Recall）的产出的结果。F1-Score的取值范围为0～1，1代表模型的输出结果最好，0代表模型的输出结果最差，其计算式如下：

6.3 结 果

在神经网络模型的调试过程中，为了找到模型最优的超参数，对模型的学习率、num_features以及卷积核的大小等超参数进行调参，不断地优化网络结构，提高卷积神经网络模型的性能，提升模型的精确性。本文利用Tensorflow框架中的Tensorboard可视化工具，用曲线图显示各参数随着运行时间以及迭代次数的变化趋势。

图3和图4分别为VGG-16网络模型和基于迁移学习的VGG-16网络模型的图像分类情况的准确率和损失图，反映了基于卷积神经网络的芯片连接丝、焊盘以及焊球的分类的损失函数随迭代次数的变化趋势。图中的准确率是由式（5）计算得到的，损失函数是根据式（4）得出的。从损失图中可以看出，两种模型都可以很好地进行收敛，损失值都是持续减少并趋向稳定，可以得到比较好的预测结果。

图5是两种模型在训练集与测试集3 ∶1的情况下芯片焊盘、焊球以及连接丝图像三分类结果的混淆矩阵。图5（a）为VGG-16网络模型的混淆矩阵，图5（b）为基于迁移学习的VGG-16网络模型的混淆矩阵。从图中可以看出，芯片焊盘、芯片焊球以及芯片连接丝的分类准确率都较高，两种模型的准确率都达到了90%以上。通过式（5）计算，最终可得出：VGG-16网络模型的准确率为93.3%，而基于迁移学习的VGG-16网络模型的准确率为98.3%。两种不同模型的F1-Score、精确率以及召回率如表3所示。由此可见，改进后的网络模型对芯片引脚、焊盘以及焊球的分类效果要优于VGG-16网络模型。

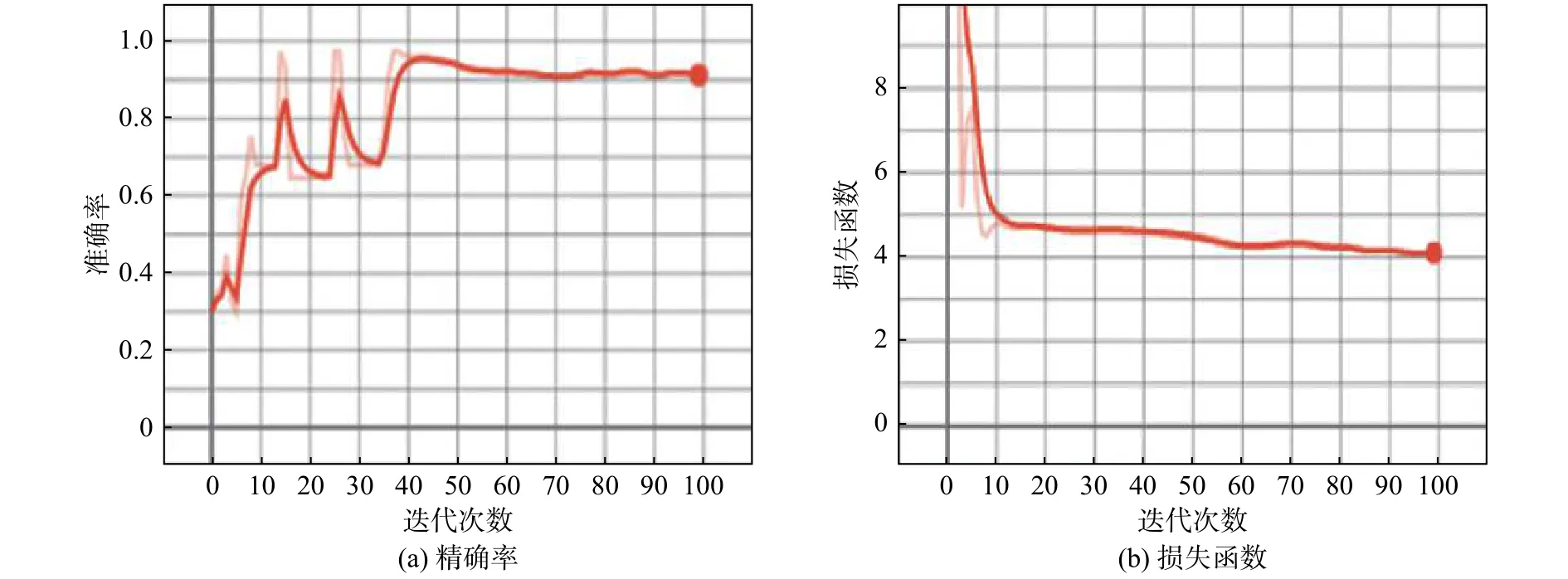
图3 VGG-16 网络模型的损失图和准确率图Fig. 3 Loss and accuracy of VGG-16 network model

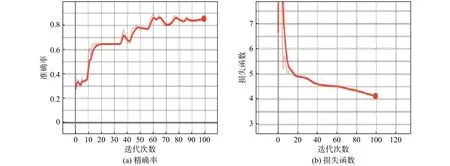
图4 基于迁移学习的VGG-16网络模型损失图和准确率图Fig. 4 Loss and accuracy of migration learning model based on VGG-16 network

图5 两种不同模型的混淆矩阵Fig. 5 The confusion matrix of two models

表3 评价指标Tab. 3 The evaluation index

7 结 论

本文提出了一种基于迁移学习的VGG-16网络模型，以此对芯片图像进行分类。实验使用前馈方法对已经在ImageNet数据集中优化过的较低层VGG-16网络的权值进行了修正，并在构建的芯片图像数据集中，使用反向传播对VGG-16上层网络的权值进行了再训练。采用VGG-16网络模型与本文提出的方法对芯片焊盘、焊球及连接丝三分类图像数据集进行了比较。实验结果表明，本文提出的方法对芯片焊盘、焊球以及连接丝的分类效果要优于VGG-16网络模型。