统计学在填埋场地下水污染指标间相互关系及水质污染程度中的应用研究

马媛 张馨月

（北京市城市管理研究院，北京 100028）

1 引言

近年来，随着城市发展，人口激增，垃圾产生量逐年递增，致使城市废弃物的排放量超过了环境的自净能力，造成了一系列地下水污染问题。目前，北京市乃至全国的城市生活垃圾处理方式仍以填埋为主［1］，填埋工程构筑简单，建设和运行费用较低，但同时会产生如填埋气、渗滤液等诸多环境污染问题。垃圾渗滤液是垃圾在堆放和填埋过程中，由于发酵和雨水的淋浴、冲刷以及地表水和地下水的浸泡而渗沥出来的污水，含有填埋场内部几乎所有的可溶物质；一些有毒物质也能够渗入地下含水层，污染地下水［2］。地下水质恶化及地下水资源保护的研究也越来越得到了人们更多的重视。如不妥善处理，很可能对北京市供水质量产生巨大影响，进而加剧北京市水资源短缺的危机，甚至会威胁周围居民的人身健康。

我国的地下水环境质量评价工作开展较晚，就目前而言大多也是对单一污染物进行分析评价，而对污染物间的相互关系以及污染系数的综合性权重考虑较为欠缺，而统计学方法在数据处理分析等技术领域已经发展得较为成熟。因此，本文重点研究运用统计学方法分析地下水中主要污染指标的适宜性，以及如何综合考虑各项指标的污染影响及污染程度。

本文选取北京市某垃圾填埋场的5 眼地下水监测井作为采样点，其中本底井1 眼、污染扩散井2眼、污染监视井2 眼。检测项目共21 项，检测频次为每月1 次，从2014 年至2017 年连续监测（其中2015 年4 月、5 月和2016 年9 月、10 月未检测），共累计获得220 组分析样本，依据《地下水质量标准》对21 项检测指标进行等级评价，确定总硬度、氨氮、高锰酸盐指数、溶解性总固体、亚硝酸盐氮、硫酸盐、硝酸盐氮、氯化物8 项指标为该填埋场主要特征污染物，根据数据本身的适用性和分析的目的性，选择运用SPSS 统计学方法对污染物间相关性和主成分因子分析进行进一步研究。

2 相关性分析

对该填埋场220 组分析样本中8 种主要污染因子进行相关性分析，观察变量之间变化趋势的一致性，输出结果见表1。

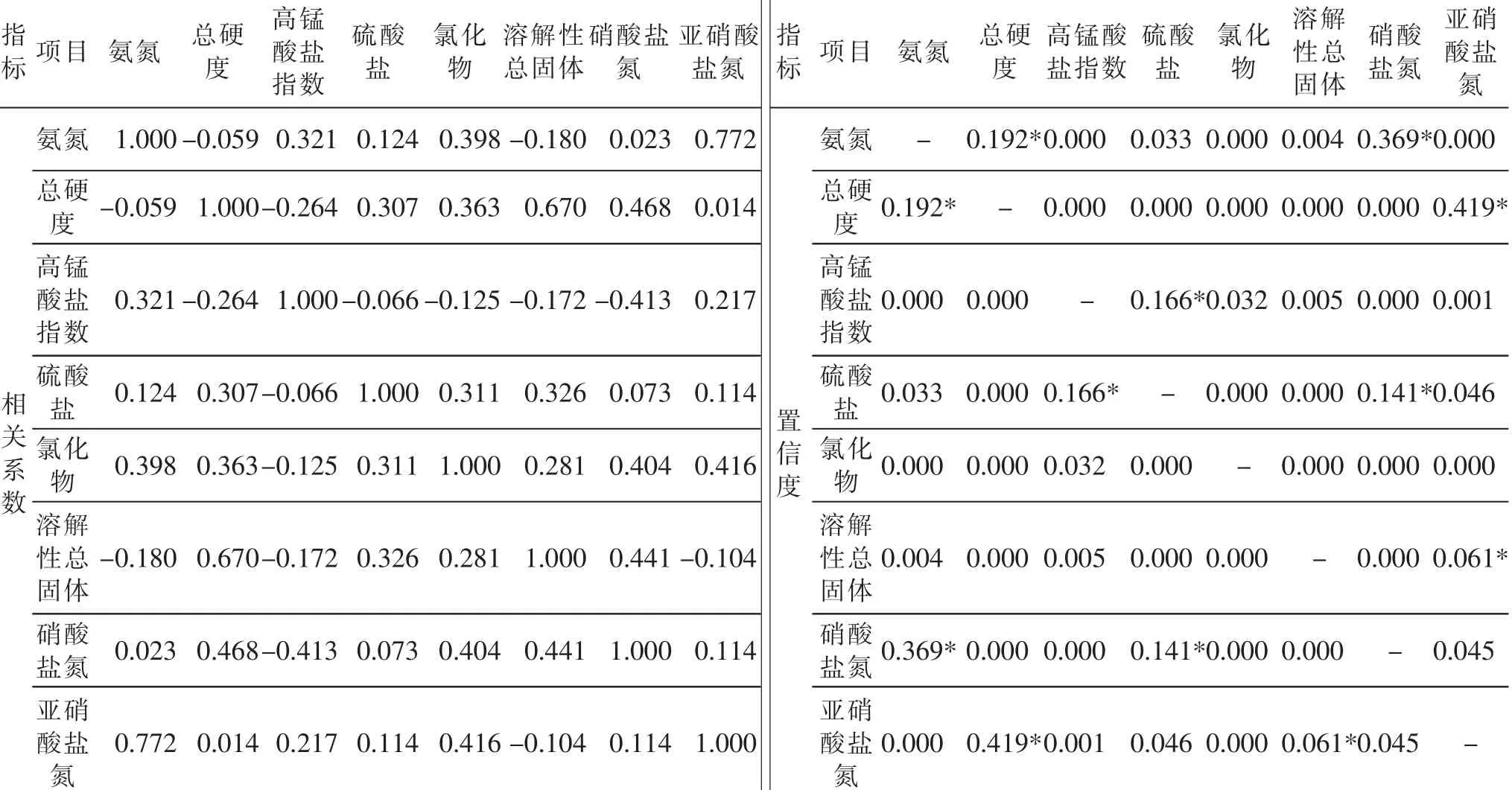
表1 初始变量的相关矩阵

表1 分为2 部分，左半部是初始变量的相关矩阵，用字母r 来代表相关性，当｜r｜＜0.3 时，表示微弱相关；当0.3＜｜r｜＜0.5 时，表示低度相关；当0.5＜｜r｜＜0.8时，表示显著相关；当0.8＜｜r｜＜1.0 时，表示高度相关［3］。根据输出结果，可以判断各分析指标间存在一定的相关性，其中氨氮和亚硝酸盐氮2 项指标间相关性达到0.772，总硬度和溶解性总固体2 项指标间的相关性达到0.670，均为显著相关的程度。

表1 右半部是各相关性对应的置信度指标，在输出结果中，带“*”标注的表示置信度大于0.05，其他不带“*”的表示置信度均小于0.05。置信度小于0.05 说明具有95%以上的可信度，由表1 可见，大部分输出结果置信度均小于0.05，表明各分析指标间的相关性可信度较高，选择相关性对样品进行分析较为适用。

另外，为了验证样品采用相关性分析的可信度，还对样品进行了KMO 统计量和Bartlett 的球形检验，检验结果见表2。

表2 KMO 和Bartlett 的检验

当KMO 统计量高于0.9 时，表示效果最佳；在0.7～0.9 间，表示效果较为理想；在0.6～0.7 间，表示效果尚可，在0.5～0.6 间，表示效果较差；在0.5 以下时，表示不适宜。

本文选取的样品在进行KMO 统计量检验时，测量取样的适当性为0.675，说明采用相关性对样品进行分析效果尚可。在进行Bartlett 球形检验时，显著性小于0.01，可以否定相关矩阵为单位阵的零假设，认为各分析指标间确实存在着显著相关性。因此，可以说明利用此方法分析地下水中主要污染指标间的相关性较为适宜。

3 主成分因子分析

通过上述相关性分析及显著性验证，论证了基于主成分分析的方法进行因子分析的充要性。因子分析主要是采用降维的思想，将多个测量变量转换为少数几个综合指标，通过归并公因子，从而降低分析问题的复杂性。采用公因子方差提取的方法，得到8 项主要污染物的共同度，结果见表3。

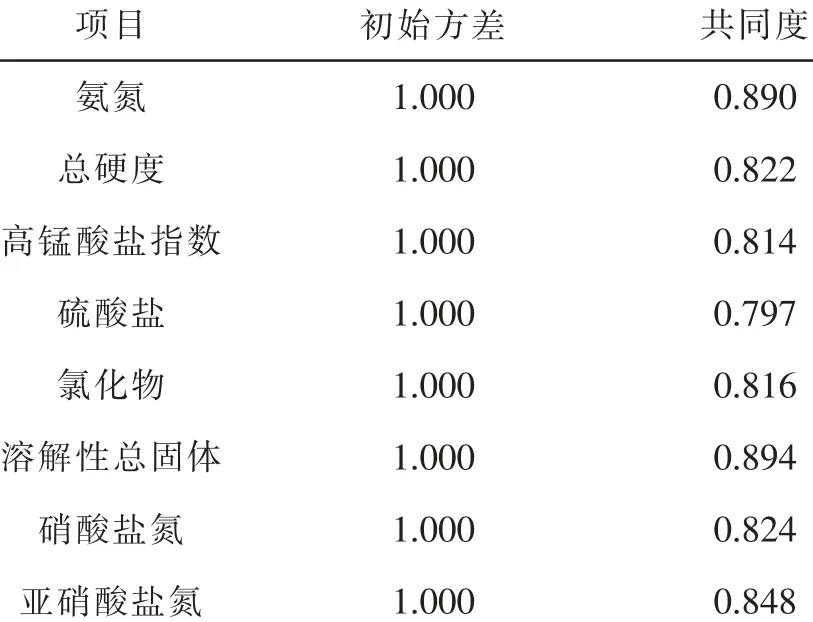
表3 公因子方差

从表3 可知，氨氮的共同度为0.890，可以解释为通过主成分提取的公因子能够解释氨氮方差的89.0%，其他项目同理。文献资料中显示，累计方差贡献率大于85%时，基本可以保证不会丢失太多重要信息［4］。再通过对主要污染物的方差进行计算，可以得到初始特征值和旋转后载入值的方差贡献率及累计贡献率，输出结果见表4。

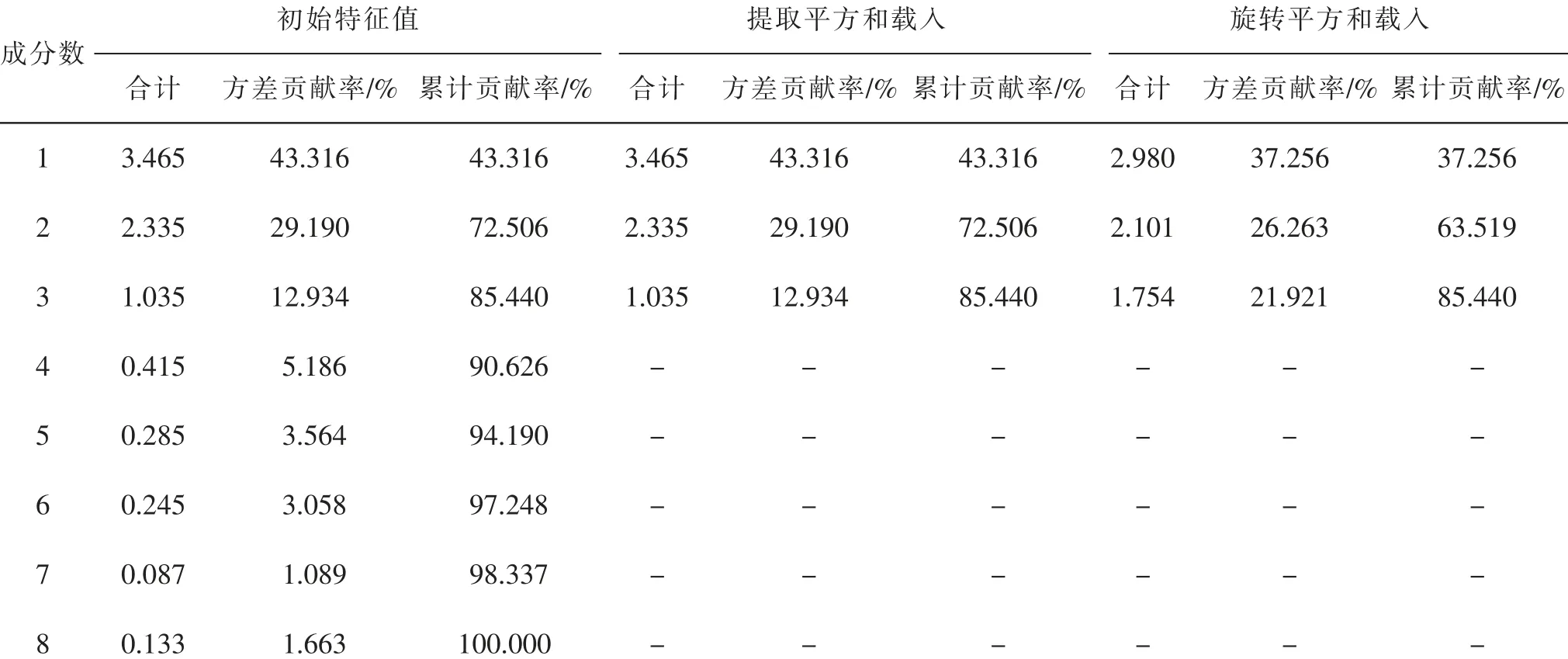
表4 提取的公因子可解释的总方差

从表4 可以看出各成分提取的方差贡献率，当提取3 个公因子时，累计贡献率为85.440%，即总体多于85%的信息可以用提取的这3 个公因子来解释，而第3 个公因子以后的成分特征值变化趋于平缓，说明提取3 个公因子比较恰当。归并后的公因子，每个公因子分别代表空间的一个维度，通过正交旋转法，可以认为各个维度之间是不相关的，这3 个公因子能够相对完整地表示各成分的体系维度，采用方差最大化正交旋转前后的因子载荷阵，主成分矩阵见表5。

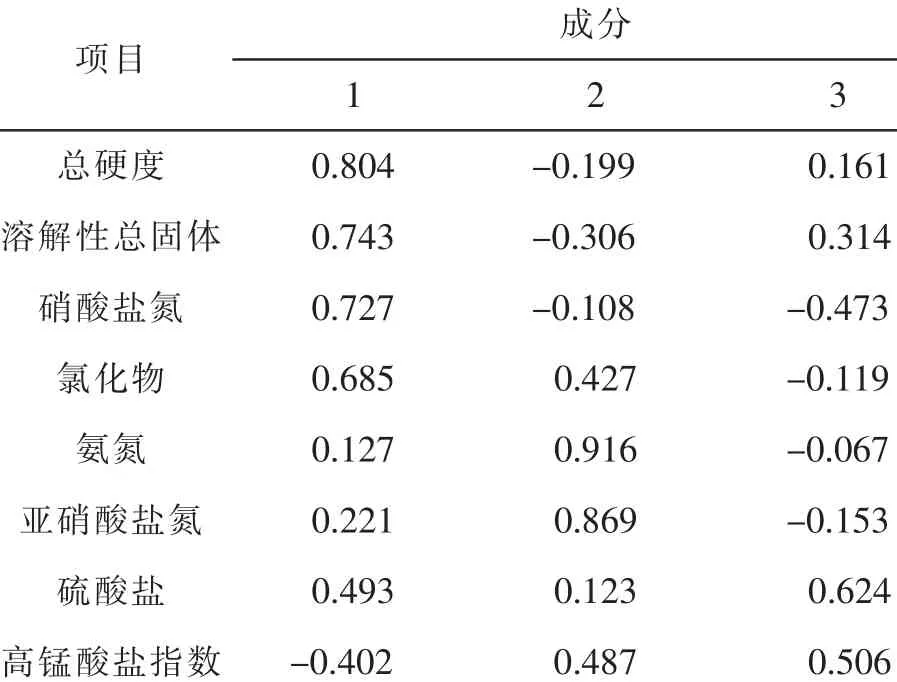
表5 主成分矩阵a

旋转成分矩阵见表6。

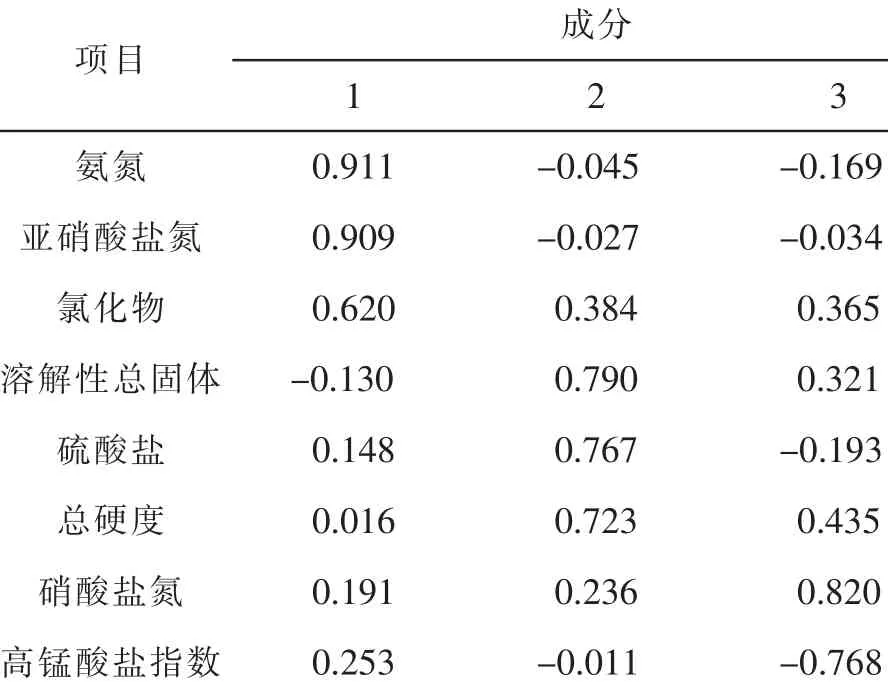
表6 旋转成分矩阵a

对某一单一物质来说，载荷绝对值越大，它与公因子的关系也越密切，能够更好地解释这个物质［5］。基于这个观点，第1 个公因子更能代表氨氮、亚硝酸盐氮、氯化物这3 项指标；第2 个公因子更能代表溶解性总固体、硫酸盐、总硬度这3 项指标；第3 个公因子更能代表硝酸盐氮、高锰酸盐指数这2 项指标。因此可以利用所提取的3 个公因子分别描述各时段各监测点位的污染状况。同时，可以进一步得到3 个公因子对各污染物影响的权重，结果见表7。

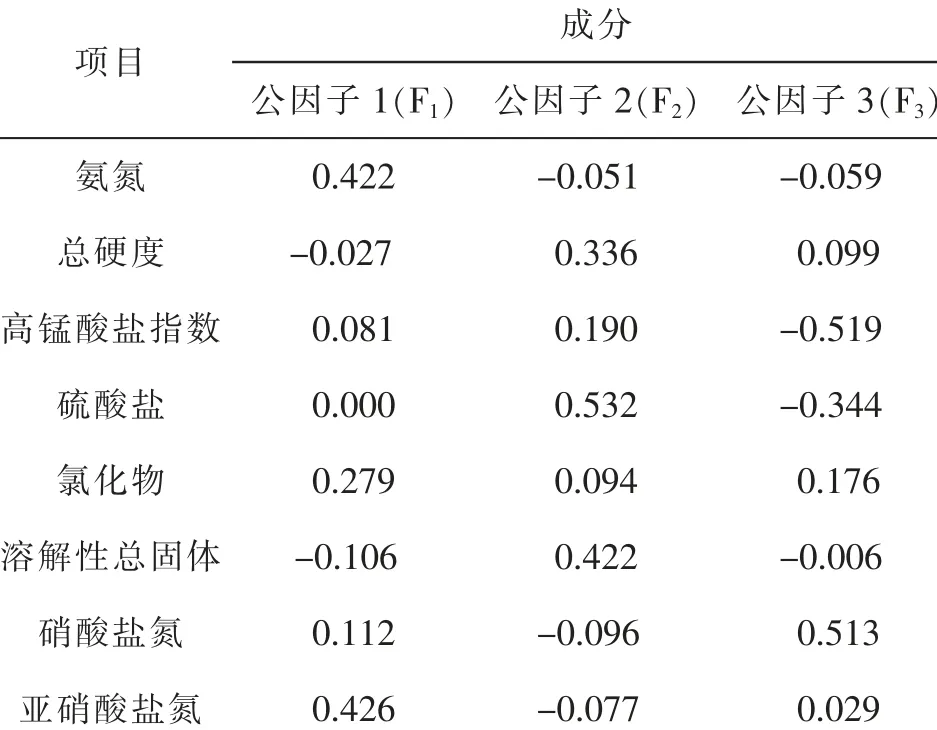
表7 成分得分系数矩阵

根据表7 可以推导出3 个公因子与各污染物间的计算公式：

为了直观地反映该填埋场各时段各监测点地下水受污染情况的综合影响，对3 个公因子进行加权求和，权数为表4 中3 个公因子旋转后的方差贡献率，依次为37.26%，26.26%，21.92%，可得综合得分计算公式：

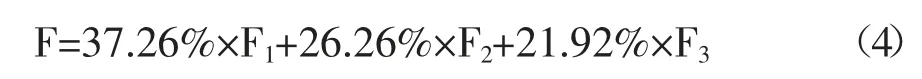
分别将220 组检测数据，按公式（1）～（4）代入计算，统计各时段各监测点位的综合得分与各公因子得分，综合得分及排名以及各公因子得分及排名情况，可以反映该填埋场各监测点位地下水水质受污染的程度。其中，第1 因子得分高的主要是受氨氮、亚硝酸盐氮、氯化物的影响较为明显；第2 因子得分高的主要是受溶解性总固体、硫酸盐、总硬度的影响较为明显；第3 因子得分高的主要是受硝酸盐氮、高锰酸盐指数的影响较为明显。

在各时段各监测点位综合得分的基础上，按照年份、监测点位、降水周期对综合得分进行平均计算，计算结果见表8。综合得分越高，表示地下水受污染程度越重，根据综合得分情况进行排名，综合排名越靠前表示水质受污染程度越重。结果显示，2017年枯水期下游污染监视井综合得分最高，另外，得分较高的还有2016 年枯水期污染监视井及2017 年枯水期本底井、枯水期和平水期的污染扩散井。

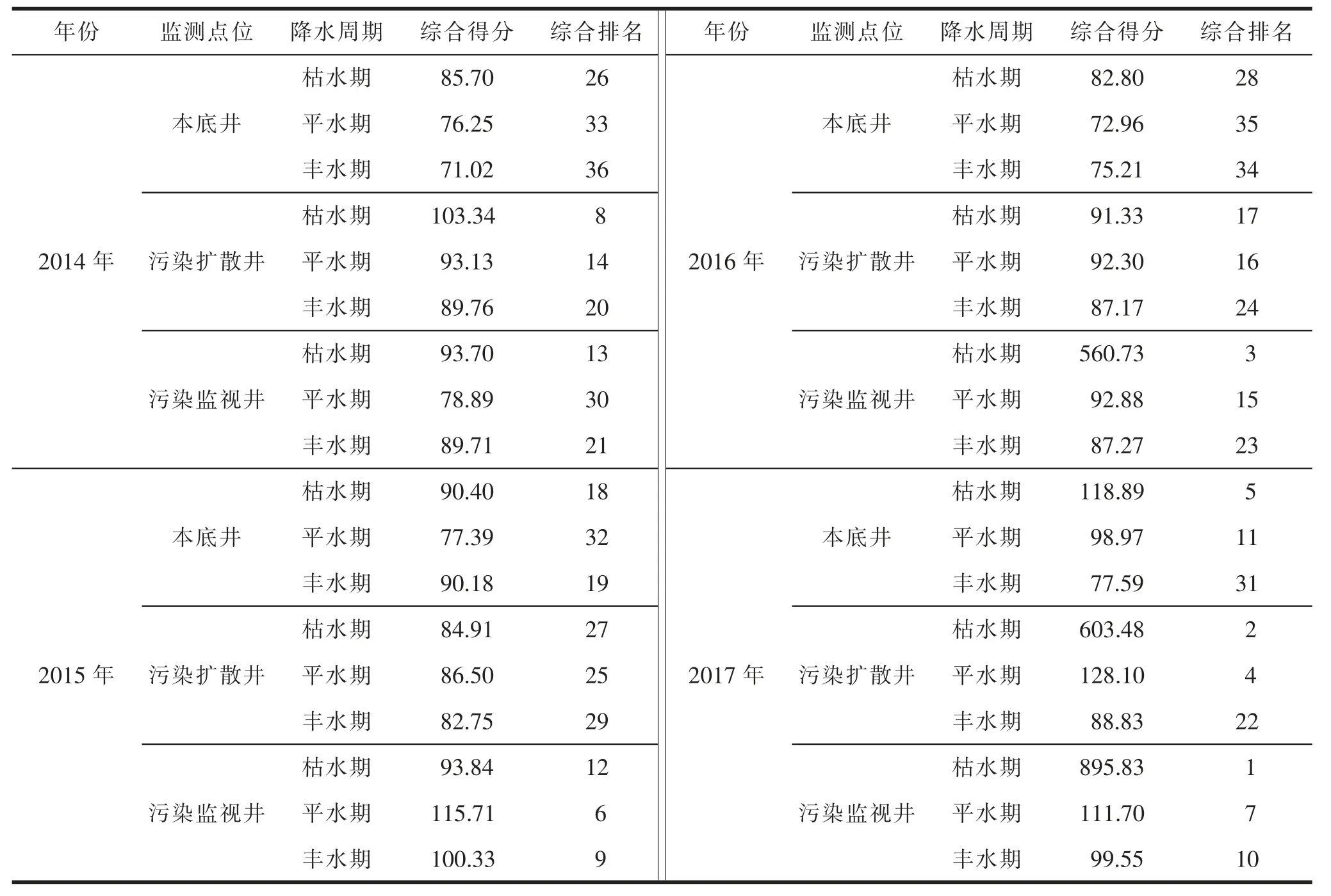
表8 各监测点位综合得分及排名

综上所述，从自然年份来看，污染程度有逐年加剧的趋势；从监测井功能来看，污染监视井污染程度高于污染扩散井高于本底井；从降水周期来看，一般枯水期污染物浓度会有升高的规律，主要是由于填埋场周边以浅层地下水为主，受降水、气候、地表水质影响较大，在枯水期时地下水补给作用会减缓，污染物含量增高，自净作用下降，水质容易变差。

公因子得分公式计算的结果，与填埋场实际监测情况的一致性较好，说明通过统计学分析方法能够对实际检测结果和复杂的化学物质间相互作用关系进行合理的分析、解释，因此，可以利用提取的3个公因子和综合得分来概括性描述各监测点位的主要特征污染物及其变化规律。

4 结论

本文在长期对垃圾卫生填埋场地下水开展监测工作，获得大量监测数据的基础上，运用统计学方法分析研究地下水中主要污染物间的相互关系及污染影响程度，得到如下结论：

（1）通过相关性分析及显著性验证，得到了主要污染物间两两相关程度，相关性越高表示相互间变化趋势越明显，其中氨氮和亚硝酸盐氮2 项指标间相关性达到0.772，总硬度和溶解性总固体2 项指标间的相关性达到0.670，均为显著相关，可以说明主要污染物间并不是独立存在的，因此在分析污染物时应综合考虑多项污染指标的共同影响。

（2）基于主成分因子分析，当提取3 个公因子时，累计贡献率超过85%，即采用此分析方法，实现了降维的效果，将8 项主要污染物归并为3 个公因子。

（3）根据各特征污染物对3 个公因子的贡献率和公因子权重，推导出因子得分公式，综合得分排名越高，表示受污染程度越重，结果显示，2017 年枯水期下游污染监视井综合得分最高，其受污染程度也最重。

（4）根据各监测点位的得分情况来看，该填埋场地下水水质污染程度有逐年加剧的趋势；从监测井功能来看，污染监视井的污染程度最为明显，要高于污染扩散井和本底井；从降水周期来看，通常枯水期污染物浓度高于平水期和丰水期，说明填埋场地下水污染程度与监测井位置和降水周期均有一定关系。