非线性泛函积分微分方程的多步龙格-库塔方法的耗散性

张 艳

(上海大学理学院,上海200444)

物理学和工程学中的很多动力系统都具有有界吸收集(即系统解的轨迹在有限的时间内进入且保持在该集合内)这一特征,因此耗散性在动力系统中占有重要的地位[1].在对这些系统数值方法的研究中,学者们希望所用的数值方法仍能保持系统解析解的耗散性,即数值方法也具有系统相应的耗散性.

在过去的几十年里,许多学者已经广泛地研究了Volterra泛函微分方程这类特殊动力系统的解析解和数值解的耗散性.Hill[2]和Humphries等[3]利用(强)A-稳定性理论或G-稳定性理论研究常微分方程(ordinary differential equation,ODE)的耗散性及相应的线性多步法、单支近似法及龙格-库塔方法等数值方法的耗散性.Huang等[4]利用代数稳定等理论给出了时滞微分方程(delay differential equation,DDE)系统的多步龙格-库塔方法、线性多步法、单支方法等数值方法的耗散性,尤其讨论了分别在有限维和无限维系统下的(k,l)-代数稳定的不可约多步龙格-库塔方法的耗散性的充分条件,并给出相应的证明.不仅如此,Wang等[5]研究了非线性中立型延迟积分微分方程系统的数值耗散性,并且给出了(k,l)-代数稳定的不可约多步龙格-库塔方法的耗散性的充分条件及相应的证明;此外,还利用复合积分公式对积分部分进行离散化处理.另外,还有一些学者[6-11]给出了Volterra泛函微分方程的系统耗散性及相应数值方法的耗散性,如时滞积分微分方程(delay integral differential equation,DIDE)、中立型时滞微分方程(neutral delay differential equation,NDDE)、中立型时滞积分微分方程(neutral delay integral differential equation,NDIDE)等.

本工作对非线性泛函积分微分方程(nonlinear functional integral differential equation,FIDE)的数值耗散性进行了研究.Zhang等[12]和Qin等[13]不仅利用复合积分公式在非经典的Lipschitz条件下给出了这类问题的龙格-库塔方法的全局稳定性结论,而且针对FIDEs问题给出了单个方法(弱)的全局稳定性结果及G-稳定的扩展向后差分(backward differentiation formula,BDF)法的全局且渐进稳定性结果.Wen等[14]和Liao等[15]关于这类问题研究了在适当条件下的代数稳定的龙格-库塔方法的耗散性及G(c,p,0)-代数稳定的单支方法的耗散性.本工作的目的是研究针对非线性泛函积分微分方程系统的多步龙格-库塔(multistep Runge-Kutta,MRK)方法的耗散性.这里,多步龙格-库塔方法不仅是在单个方法、线性多步法和龙格-库塔方法的基础上的推广,而且也是广泛的混合法.

1 非线性泛函积分微分系统的描述及耗散性

1.1 FIDEs系统

令Cd表示带有内积⟨·,·⟩的d-维复欧几里得空间,其相应的范数为∥·∥,在Cd×d空间中的矩阵范数∥·∥服从于向量范数的定义.对于任意实对称p×p阶矩阵Q=[qij],Q>0(>0),即矩阵Q是非负的(正定的).

对任意Q>0,在(Cd)p=Cdp上定义一个伪内积:

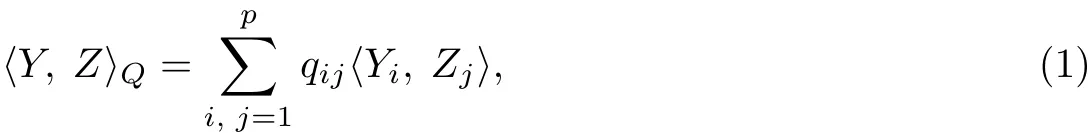
相应的伪范数为

式中:Y=(Y1,Y2,···,Yp)∈ Cdp;Z=(Z1,Z2,···,Zp)∈ Cdp. 很显然,当Q>0时,式(1)和(2)分别表示Cdp上的内积和范数.当矩阵Q为单位阵时,∥·∥Q可简写为∥·∥.

在本工作中,考虑如下非线性泛函积分微分方程系统:

式中:τ>0为给定常值时滞;函数f:[t0,+∞)×Cd×Cd→Cd是除第一个变量外关于其他变量的局部Lipschitz连续函数;g:D×Cd→Cd是一个连续函数;φ:[t0−τ,t0]→Cd是一个连续函数.假定系统(3)有唯一解y(t),且函数f和g满足如下条件:

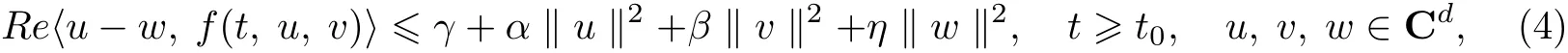
且

式中:γ,α,β,η,λ为给定实值常数,且γ,−α,β,η为非负的,λ >0,2λτ<1,

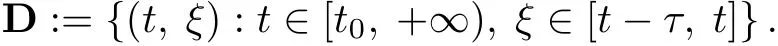
为了研究系统(3)的数值耗散性,这里假定函数f满足如下条件:对任意常数M>0,存在L=L(M)>0,使得对于∀成立.

1.2 FIDEs耗散性

定义1[14]如果存在一个有界集B⊂Cd,对任意给定的有界集Φ⊂Cd,存在一个时刻t∗=t∗(Φ),使得在任意给定的连续初始函数ϕ :[t0− τ,t0]→ Cd(对于∀t∈ [t0− τ,t0],ϕ(t)包含在Φ内)下系统(3)所对应的相应的解y(t)对所有的包含在集合B内成立,那么FIDEs系统(3)被称为在Cd上是耗散的.这里,B称为Cd内的吸收集.

引理1[14]假定y(t)是系统(3)的一个解,且其中的f和g分别满足条件(4)(α<0)和(5).若存在一个常数0<δ<1,使得

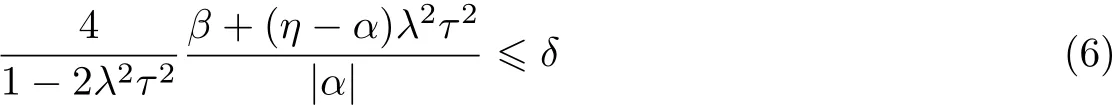
成立,那么有

(1)对于∀t>t0,有

γ,α,β,η,λ均由条件(4)和(5)给出.

(2)对于∀ε>0,存在t∗=t∗(ϕ,ε),使得

成立,因此系统(3)是耗散的,且吸收集为

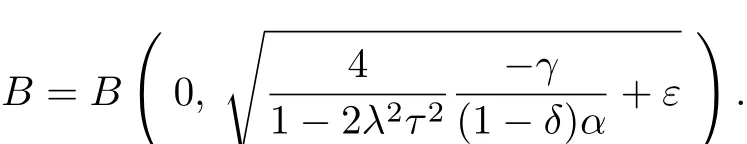
2 数值方法(MRK法)

2.1 ODEs系统的MRK法

常微分方程(ODEs)的s-级r-步龙格-库塔方法可以写成如下形式:

式中:h>0为固定步长;系数aij,bij,θj,γj和Cj均为实值常数;tn=nh(n=0,1,···),Y(n)i和yn分别是y(tn+cih)和y(tn)的近似,为了简化起见,假定0 6 ci6 r,i=1,2,···,s.这里,多步龙格-库塔方法是一般线性方法的一个子类.

为了简化多步龙格-库塔方法的形式,令

C11=[bij]∈ Rs×s, C12=[aij]∈ Rs×r,

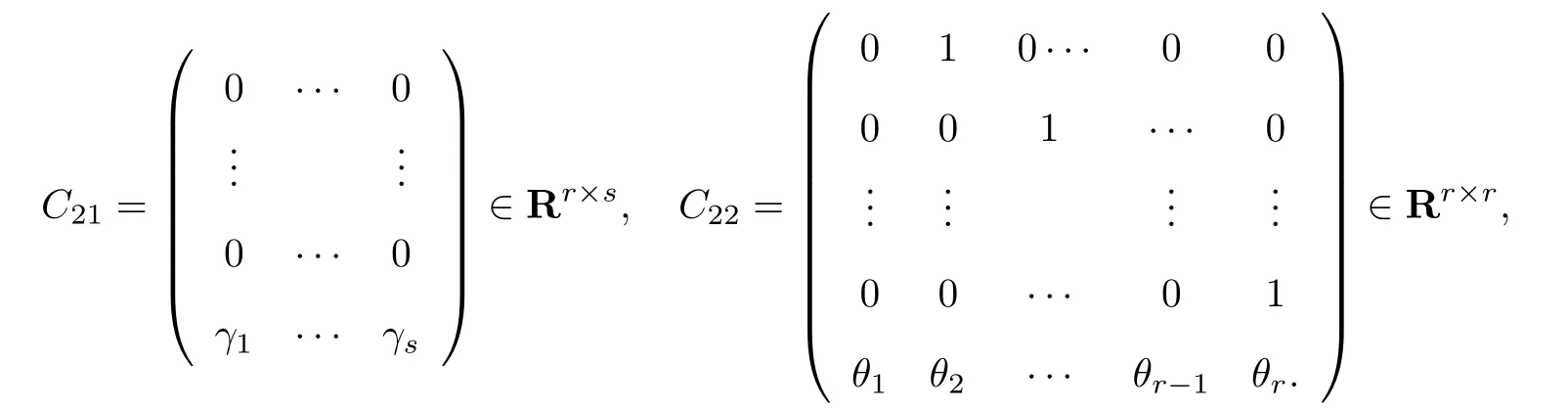
对于任意给定的k×l实矩阵Q=[qij],接下来定义相应的线性算子Q:Cdl→Cdk,

其中,

从而,方法(7)可以写成如下一般线性法的形式:

这里,

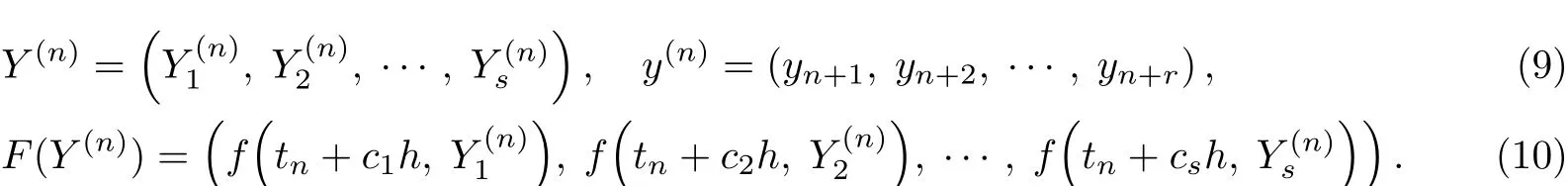
2.2 FIDEs系统的MRK法

利用多步龙格-库塔方法(7)可以得到问题(3)的多步龙格-库塔方法的形式:

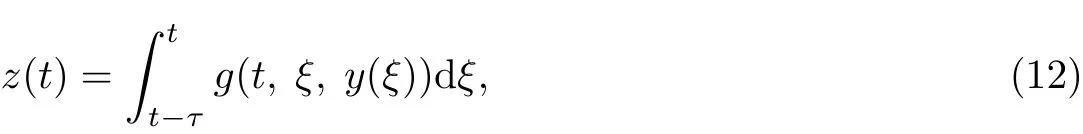
和

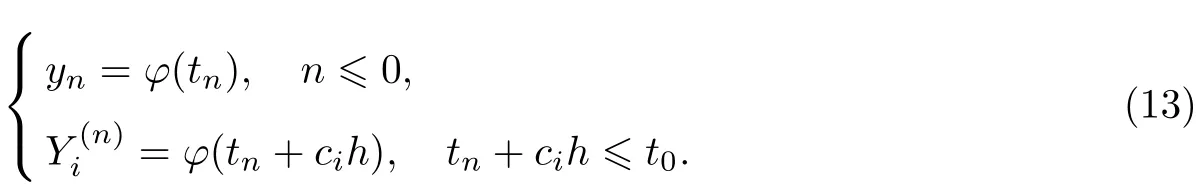
这里,对于积分部分zn,,应用复合积分公式来进行求解,即

这里的求积公式(14)和(15)可以由一个统一的叠加规则得到[6,12-13].为了对数值耗散性进行分析,假定式(14)和(15)也满足下面条件

式中:mh=τ且σ为正常数.这里方法(11)还可以写成如下一般线性法的形式:

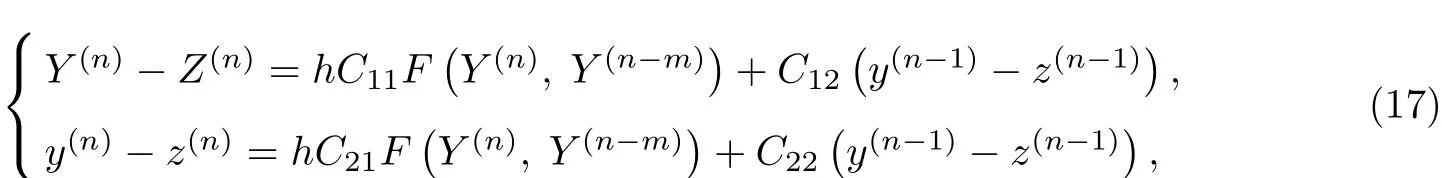
其中,

为了对数值耗散性进行分析,这里给出如下相关定义.

定义2[5]对于给定的实值常数k,l,如果存在一个实对称的r×r矩阵G>0和对角矩阵D=diag(d1,d2,···,ds)>0,使得M=[Mij]>0成立,则称数值方法(8)为(k,l)-代数稳定的.这里

特别地,当k=1,l=0时,(1,0)-代数稳定简称为代数稳定的,其中

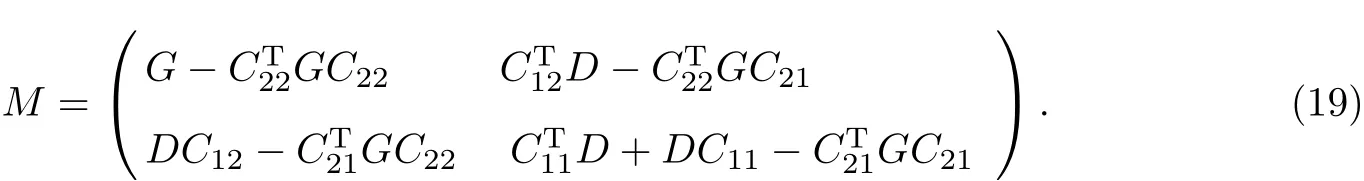
本工作将利用(1,0)-代数稳定性来分析数值耗散性.

定义3[5](1)如果在形如式(7)的多步龙格-库塔方法中对于某些非空指标集T⊂{1,2,···,s},有

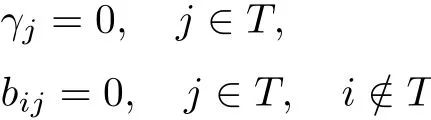
成立,则称该方法为阶段可约的;否则,称其为阶段不可约的.

(2)如果在形如方法(7)的多步龙格-库塔方法中的多项式有公因子,则称该方法为步可约的,其中

否则,称其为步不可约的.

(3)如果形如方法(7)的多步龙格-库塔方法是阶段可约的或者是步可约的,则称该方法为可约的;否则,称其为不可约的.

下面,给出多步龙格-库塔方法的耗散性定义.

定义4 如果方法(11)以步长h适应于形如系统(3)的动力系统且满足条件(4)和(5)且存在一个常数R, 使得对任意的初始函数φ(t)及任意初值Y(−m),Y(−m+1),···,Y(−1)和y0,y1,···,yr−1,存在一个n0=n使得

成立,则称数值方法(11)为耗散的.

3 MRK方法的数值耗散性

在对多步龙格-库塔方法的数值耗散性进行分析之前,先给出以下2个引理.

引理2[5,16]假设阶多项式的一组基且在阶严格小于q的多项式空间中,E为平移算子:Eyn=yn+1,则对于如下方程组系统

总存在一组唯一解yn,yn+1,···,yn+q−1,且存在一个与∆i无关的常数v,使得

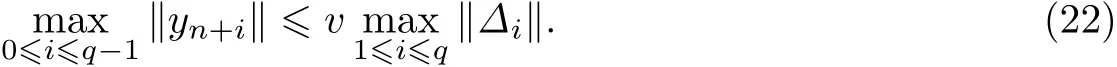
引理3[5,16]假定方法(7)是步不可约的,那么存在一组实值常数vi,i=1,2,···,s使得σ0(x)和没有公因子.

下面,给出多步龙格-库塔方法的数值耗散性定理.

定理1 假定①系统(3)满足条件(4),(5)和(6);②系统方法(7)是步不可约的且是(1,0)-代数稳定的,D=diag(d1,d2···,ds)>0,那么当α+β+ηλ2σ2<0时,关于非线性泛函积分微分方程系统(3)的数值方法(11)(满足方法(14),(15)和(16))是耗散的.

证明 类似于文献[17],通过方法的代数稳定性,易得

且有

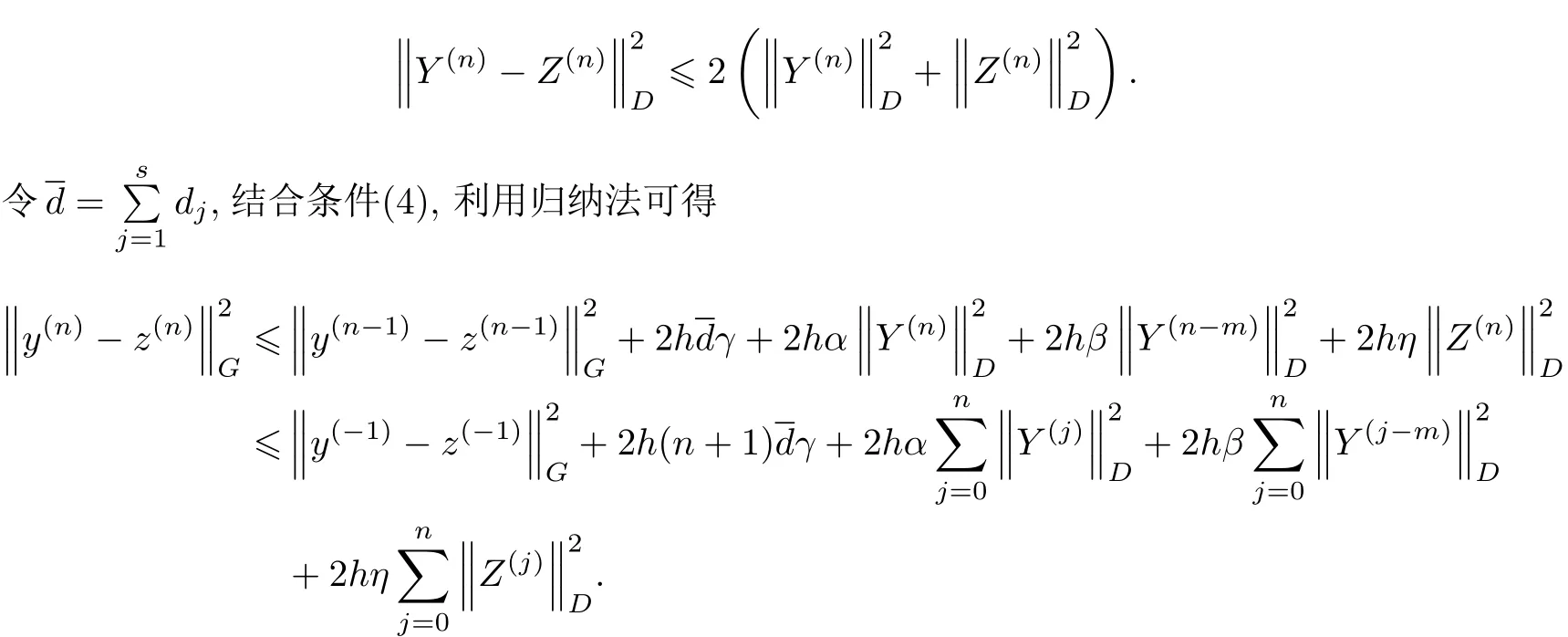
对式(15)做自身的内积,结合式(5),(16)及Cauchy-Schwarz不等式,可得

从而有

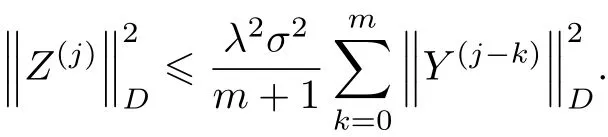
另一方面,可以推出

因此,有

这里,

取λ1为矩阵G的最大特征值,则有

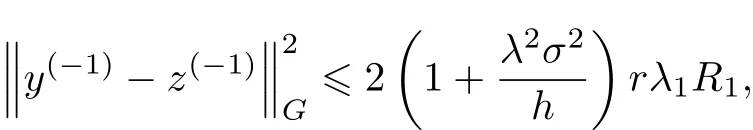
从而,有

令

则有µ>0,

当γ =0时,由式(25)及h(α+β +ηλ2σ2)<0,可得

另一方面,由方程(11)可得

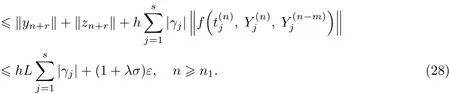
这里,

由引理3可知,存在常数vi,i=1,2,···,s,使得σ0(x)和没有公因子,从而有

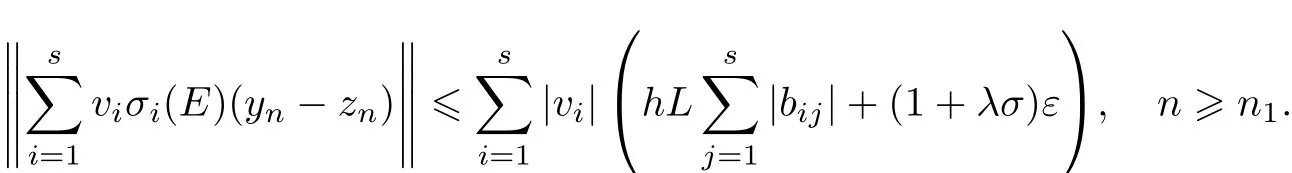
从而有

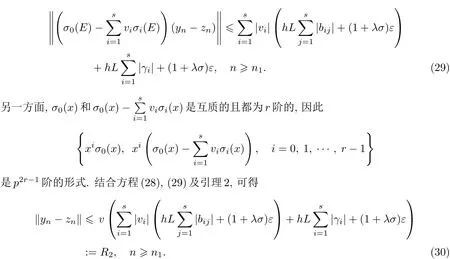
当γ>0时,利用与文献[16]相似的技术,可知存在R4>0及正整数使得

这里,

这里,λ2表示矩阵G的最小特征值;R0,R1分别由式(24)和(27)给出.

结合方程(30),(31)可知,存在一个常数R′=max{R2,R4}使得对任意初始函数φ(t)及任意初值Y(−m),Y(−m+1)···,Y(−1)和y0,y1,···,yr−1,存在,使得

接下来,我们来对∥yn∥进行估计证明.

由于

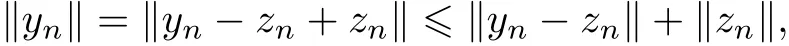
又由于其证明过程与文献[15]的定理3.1中该部分的证明过程相似.由此可知,对任意给出的ε>0,存在使得

定理得证.

通过对定理1的证明可以看出,对于任意给定的初始函数及初始值,s-级r-步龙格-库塔方法可以保持FIDEs系统的耗散性.在证明过程中借助引理2和3对多步龙格-库塔法进行了巧妙的处理,这里要求多项式部分是步不可约的,从而使得结论成立.

4 数值算例

下面考虑用多步龙格-库塔方法来解决如下2维系统:

这里,

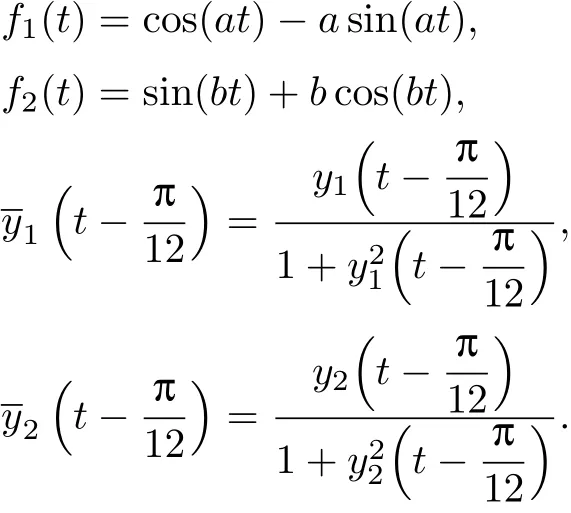
对于这个系统,选取

从而易知引理1的条件成立,则系统(33)是耗散的且对任意给定ε>0,有一个吸收集

为了解决系统(33),用如下形式的2-步1-级龙格-库塔方法来进行求解.

2-步 1-级龙格-库塔方法

易知方法(34)是代数稳定的.当应用方法(34)求解方程(33)时,只考虑在一个约束网下且利用式(14)和(15)来近似积分部分.

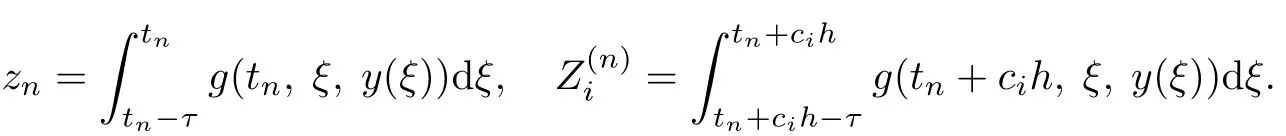
(1)y1(t)=sin(t)et,y2(t)=2t2;

(2)y1(t)=4sin(4t),y2(t)=3cos(3t).

由于方法(34)是2-步方法,因此除了需要y0外还需要一个y1.用如下2-级3-阶龙格-库塔方法来计算:相应的数值结果如图1∼6所示.

(1)当a=2,b=3,初始函数为式(1)时,问题(33)的数值解的情况(见图1).数值解yn随着时间t的收敛性情况如图2所示.

(2)当a=3,b=4,初始函数为式(2)时,问题(33)的数值解的情况(见图3).数值解yn随着时间t的收敛性情况图如图4所示.

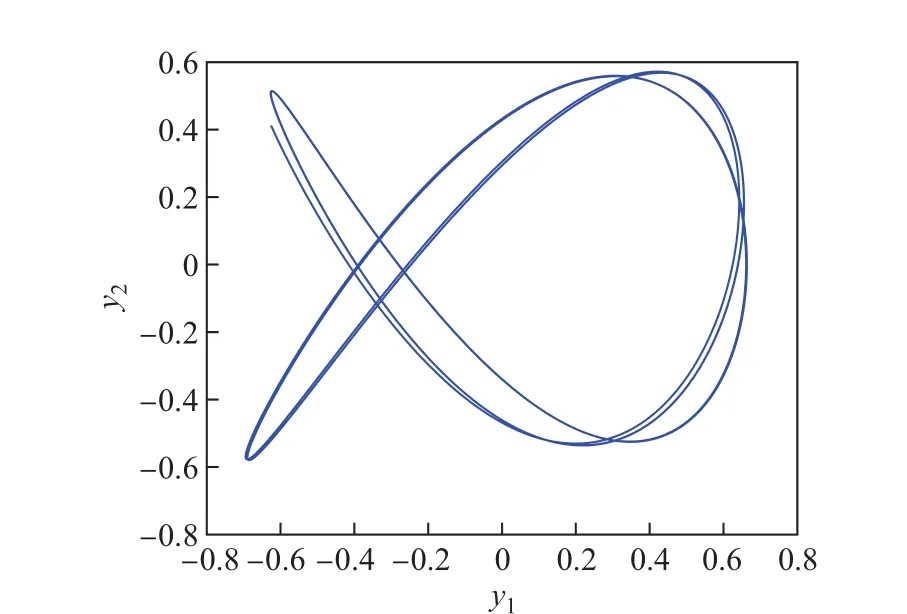
图1 h=0.004π/12,a=2,b=3,初始函数为式(1)时,问题(33)在区间[,10π]的数值解Fig.1 h=0.004π/12,a=2,b=3,when the initial function is(1),the numerical solution of the problem(33)which is in the[,10π]

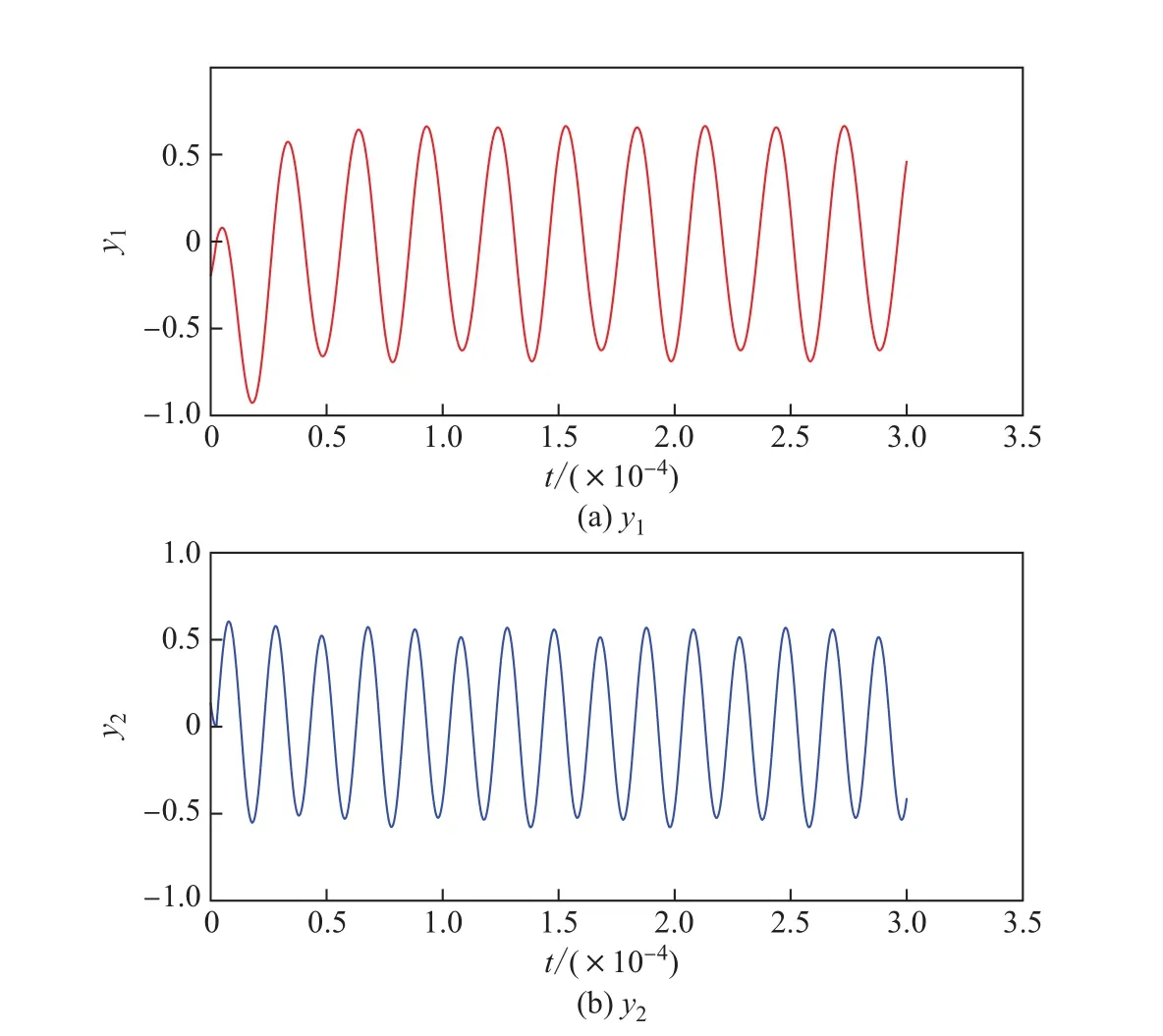
图2 h=0.004π/12,a=2,b=3,初始函数为(1)时,问题(33)在区间[,10π]的数值解随时间变化的情况Fig.2 h=0.004π/12,a=2,b=3,when the initial function is(1),the numerical solution’s changing curve of the problem(33)which is in the[,10π]

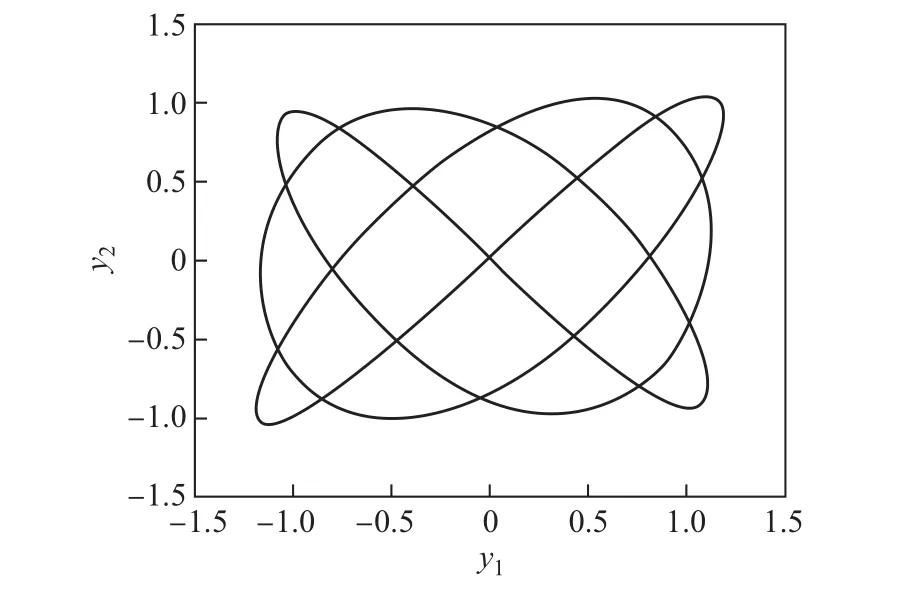
图3 h=0.004π/12,a=3,b=4,初始函数为(2)时,问题(33)在区间[,10π]的数值解Fig.3 h=0.004π/12,a=3,b=4,when the initial function is(2),the numerical solution of the problem(33)which is in the,10π]

图4 h=0.004π/12,a=3,b=4,初始函数为(2)时,问题(33)在区间[,10π]的数值解随时间变化的情况Fig.4 h=0.004π/12,a=3,b=4,when the initial function is(2),the numerical solution’s changing curve of the problem(33)which is in the[,10π]

(3)为了观察方法(35)的稳定性情况,对问题(34)给出不同的初始函数,分别得到相应的数值解yn=[y1n,y2n],zn=[z1n,z2n],再令En=∥yn−zn∥表示2个数值解的差,观察随着时间t的变化,相应的En的变化情况.

当a=3,b=4,初始函数分别为式(1)和(2)时,问题(33)的数值解的情况如图5所示,En的变化情况如图6所示.

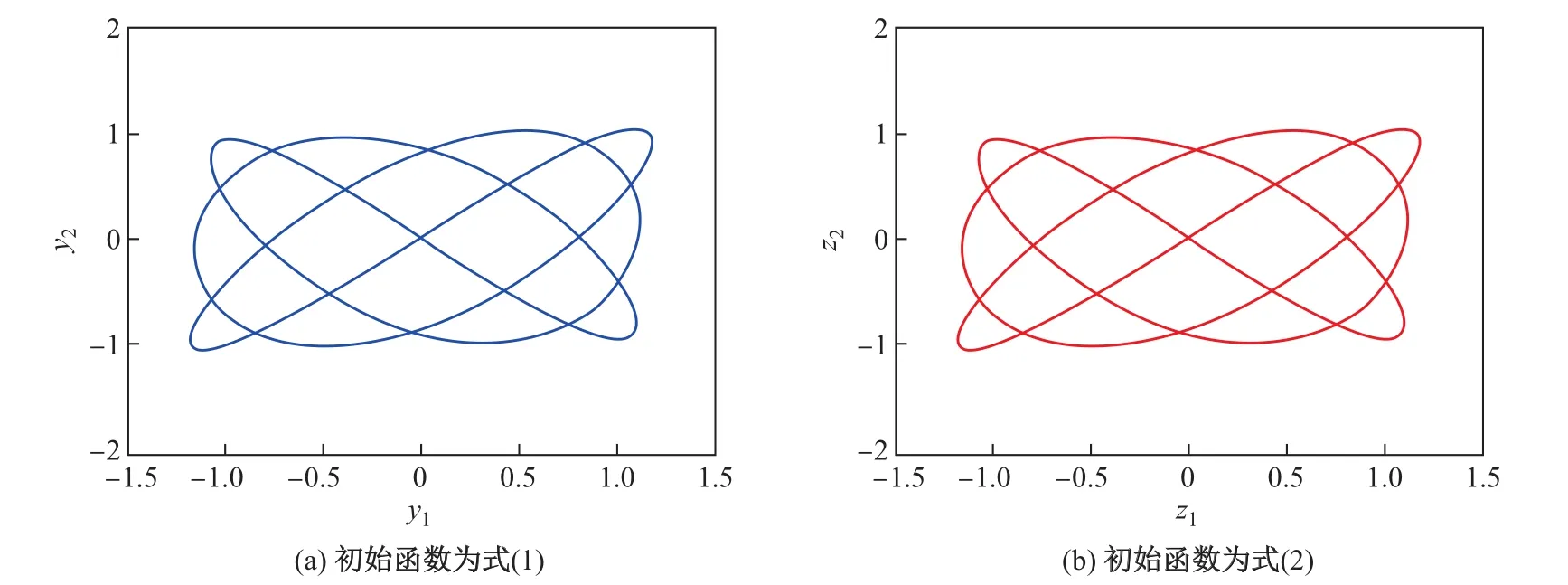
图5 h=0.004π/12,a=3,b=4,初始函数分别为式(1)和(2)时,问题(33)在区间[,10π]的数值解Fig.5 h=0.004π/12,a=3,b=4,when the initial functions are(1)and(2),the numerical solutions of the problem(33)which is in the[,10π]

图6 h=0.004π/12,a=3,b=4,初始函数为(1)和(2)时,问题(33)在区间[,10π]的数值解随时间变化的情况Fig.6 h=0.004π/12,a=3,b=4,when the initial functions are(1)and(2),the numerical solutions’changing curve of the problem(33)which is in the[,10π]

由以上数值算例可知,问题(34)是耗散的,且相应的多步龙格-库塔方法(35)也具有耗散性,从而可验证上面给出的定理结论成立.除此之外,由图6可知数值方法(35)是收敛的.

5 结束语

对于非线性泛函积分微分方程系统数值解的耗散性,本工作基于龙格-库塔方法耗散性给出了多步龙格-库塔方法的耗散性结论.无论是从理论上还是数值试验上,针对本工作给出的非线性泛函积分微分方程系统的多步龙格-库塔方法的耗散性结论都是有效的.