领导者驱动下频率权重耦合复杂系统的同步
金彦亮,朱怀清,齐 崎,周润滋
(上海大学通信与信息工程学院,上海200444)
数量庞大的相互联系、影响、作用的单元所组成的系统广泛存在于现实世界中[1].因为组成单元的相互作用和动力学行为都非常复杂,所以这类系统被称为复杂系统.复杂系统涉及统计物理学、计算机科学、生物学、社会学、非线性动力学等,已成为国内外各学科研究人员的研究热点[2].随着对复杂系统跨学科研究的大力发展和渐趋深入,复杂系统的动力学行为正成为非常活跃的研究领域之一.大量实际的复杂系统表明,经过简单耦合作用形成自发的同步是普遍存在的重要集体动力学行为.对于复杂网络上大量振子经相互耦合作用形成的复杂系统,同步产生的原因和控制手段受到了特别的关注.国外学者提出了几种振子模型来分析同步的产生,较有影响力的振子模型有Lorenz振子[3]、Kuramoto振子[4]等.
在真实世界的许多复杂系统中,振子受到相互作用的程度与振子自身特征有关.如在社交网络的复杂系统中,有相同社交圈的一个性格外向的人与一个性格内向的人,前者比后者受他人的影响更大;Do¨ofler等[5]在对智能电网的研究中也发现类似的现象,提出了将由Kuramoto振子组成的非均匀耦合网络用于电力网络的稳定性分析,这个成果促使研究人员提出了相互作用程度与振子本征频率相关的非均匀耦合Kuramoto模型[6];Liu等[7]研究了权重指数对频率权重耦合网络的动力学行为的影响;Zhang等[8]研究了频率权重耦合的一般复杂网络的同步;Xu等[9]对频率权重耦合的全联网的同步临界阈值进行了讨论;Bi等[10]研究了具有均匀频率分布的频率权重耦合网络上的动力学行为.
通常,复杂系统受环境的影响是不容忽略的.如传感器网络节点上的时钟在参考邻节点修正以达到同步时还会参考统一的GPS时钟,因为人体细胞的昼夜节律受到光照的影响.复杂系统有时还会对外界刺激失去反应,例如大脑病变引起的癫痫等[11].外界刺激相当于对复杂系统施加了外场驱动作用,这个刺激源可以被抽象为独立的振子,称为领导者节点.目前,对于施加领导者驱动的复杂系统的研究有一定进展,如Wang等[12]研究了施加领导者驱动的Kuramoto模型的指数同步率;Zou等[13]研究了随机网络和无标度网络部分振子施加领导者驱动的情况;Yuniati等[14]讨论了噪声驱动的耦合神经网络的同步;Seshadri等[15]讨论了脉冲驱动的复杂系统.
由于复杂系统在满足一定条件的耦合强度时因振子间的耦合作用会自发同步,因此上述许多研究都关注的是这种自发的相互同步.领导者节点对复杂系统的振子施加驱动作用时,复杂系统的同步应区分不同的2种类型,即振子间的耦合作用形成的相互同步和领导者驱动作用形成的驱动同步,二者的集体动力学行为细节不尽相同.本工作提出了一种结合系统内频率权重耦合作用和系统外领导者节点驱动的、用Kuramoto振子组成的复杂系统模型,研究了当振子受到外界领导者节点的驱动时,频率权重耦合复杂系统的同步,指出了上述2种同步的区别,并给出了相互同步转变为驱动同步的条件.数值模拟结果证明了本模型所获结果的正确性.
1 Kuramoto振子和同步判据
Kuramoto振子是一种没有振幅只有相位的自维持振子,θi和ωi分别为振子i的相位和本征频率[1].以一对Kuramoto振子为例,振子间的耦合作用表示为

通常,耦合强度λ取大于0的正值.通过这种耦合作用2个振子的相位会随着耦合强度的增强趋向于相同.
对于N个Kuramoto振子组成的复杂系统,序参量r是衡量整个系统集体动力学行为特别是振子同步程度的参量,定义为

式中:ψ代表系统中振子的平均相位.系统中所有Kuramoto振子的相位可以被看作分布在一个单位圆上,当r=0时所有振子的相位平均分布在单位圆上.随着系统同步程度的增大,振子的相位将聚集在单位圆的某一点附近,r随之增大.当r=1时所有振子相位相同,系统完全同步.
2 带有领导者驱动的频率权重耦合模型
2.1 系统模型
由N个Kuramoto振子为节点组成的频率权重耦合复杂系统中,每个振子都可视为一个节点,则如果系统中的各振子间存在相互作用,则系统可被视为存在一条连接节点的边.复杂系统的网络结构为节点和边组成的集合,通常用邻接矩阵来描述.如果节点i和j间存在相互作用,则邻接矩阵的元素Aij=1;否则Aij=0.受到外界领导者驱动的由N个Kuramoto振子组成的频率权重耦合复杂系统可以描述为

式中:Aij表示为复杂系统网络结构的邻接矩阵的元素;λ为耦合强度;ki为节点的度,定义为节点连接的边数,

电网等复杂系统表明,节点受到相互作用的程度与节点自身特征有关.Kuramoto振子的本征频率绝对值反映了其活跃程度,因此式(3)的耦合项与本征频率绝对值成正比.复杂网络上的Kuramoto模型还要求对相互作用作拓扑结构上的归一化,故式(3)中耦合项除以节点度反映了振子拓扑结构上的特征.将动力学和拓扑结构的特征联系起来并作为节点的自身特征统一表征,称振子本征频率绝对值与节点度的比值为节点的频率权重.式(3)的后半部分表示领导者对第i个节点上振子的驱动作用,ω0为领导者本征频率.领导者对受影响的振子驱动强度为h,对不受影响的振子驱动强度为0,定义领导者影响的振子集合为C,则

2.2 系统的相互同步
当领导者对频率权重耦合复杂系统的所有Kuramoto振子都不施加驱动时,系统会在耦合强度满足条件的情况下因频率权重耦合作用产生自发的相互同步.以全连网为例,使用平均场方法,序参量方程(2)的虚部为
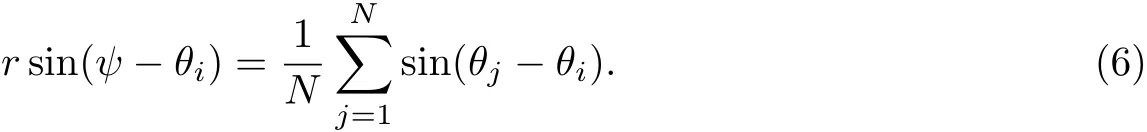
定义振子相位与网络平均相位的相位差为ϕi=θi−ψ,当领导者不施加驱动时h=0,由于全连网中ki≈N,代入式(6)重写式(3):

系统同步时振子锁相,故有

相位差正负与振子本征频率的正负相同,随着耦合强度的增大,这2种相位差的值同时接近于0.复杂系统中振子的本征频率设定为符合对称分布,故当系统同步时,集体动力学行为的有效频率相当于所有振子本征频率的平均值,该平均值为0,平均相位也为0,根据振子相位与网络平均相位的相位差公式和式(2)有

因此,当耦合强度大于2时,系统的大量振子会通过频率权重耦合作用形成大规模的相互同步簇团,序参量急剧增大;当耦合强度远大于2时,全连网和非全连网的系统都会达到相互同步.
2.3 系统的驱动同步
为了便于分析领导者对复杂系统的振子施加驱动后系统达到驱动同步的条件,根据上述结果设定复杂系统的耦合强度远大于2,使系统首先达到相互同步.同样地,分析相互同步所需条件的过程,定义振子与领导者的相位差为ϕi=θi−ω0t,则根据式(1)得到
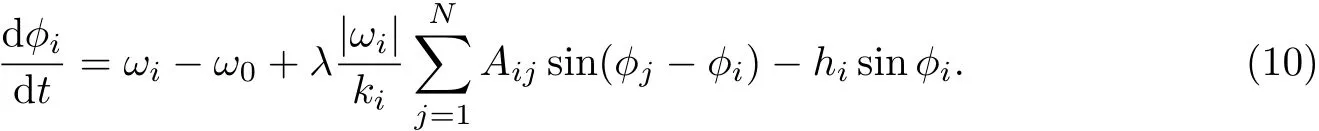
系统中有N个振子,对应N个以上形式的等式.定义振子本征频率绝对值的平均值为⟨|ω|⟩,网络的节点平均度为 ⟨k⟩,对 N 个等式等号两边同乘以 (⟨|ω|⟩/⟨k⟩)·(ki/|ωi|),N 个等式左右两边分别相加后除以N,并为方便起见定义
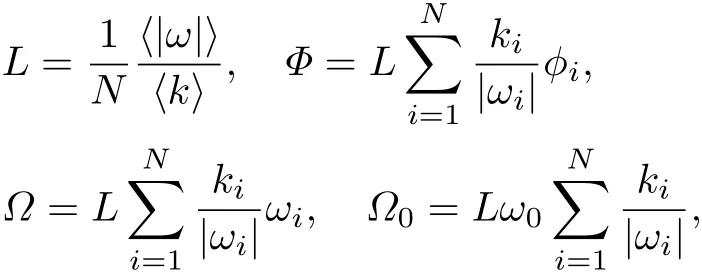
则有

式中:i∈C表示节点i属于领导者驱动的节点的集合.当网络受领导者影响达到全网驱动同步时,式(11)中ϕj=ϕi,故有
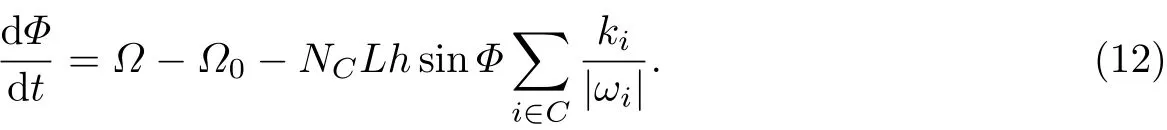
由于振子与领导者的相位差为常数,因此进一步有

设定驱动强度为正值,故可以得到使这一等式成立的领导者驱动强度的最小值为
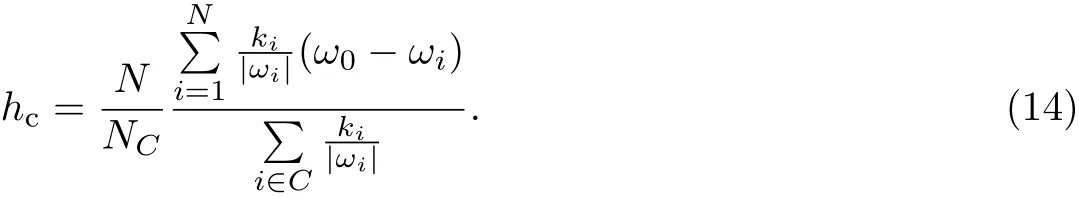
由以上结果可知,在受到外界领导者驱动的由N个Kuramoto振子组成的频率权重耦合复杂系统中,即使系统本身的耦合强度远高于使整个网络相互同步的临界耦合强度,只要领导者驱动强度满足条件,就可以使整个网络从相互同步转变为驱动同步.根据式(14)可以看出,对于一个拓扑结构和振子本征频率确定的复杂系统,这个领导者驱动强度的最小值与领导者本征频率和被驱动的振子数量和振子频率权重有关.
领导者驱动所有振子时,式(14)可以简化为
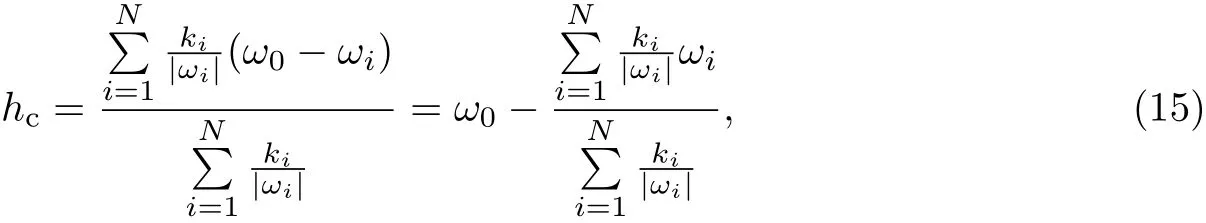
化简后的结果是领导者本征频率减去的实际上是网络达到相互同步时网络中振子的平均有效频率.对于振子本征频率符合对称分布的情况,当网络达到相互同步时网络中振子的平均有效频率约等于0,使系统达到驱动同步的驱动强度的最小值约等于领导者本征频率.
根据式(14)可知,当领导者驱动系统部分振子时,驱动的振子越多使系统达到驱动同步的驱动强度的最小值越小.在驱动的节点数量相同的情况下,驱动频率权重较大的振子比驱动频率权重较小的振子更难以使系统达到驱动同步,因为相比后者领导者需要的驱动强度变大.
3 数值模拟结果
为验证理论结果的正确性,本工作对有200个Kuramoto振子的频率权重耦合复杂系统进行数值模拟.系统的网络结构为节点平均度⟨k⟩=12的E-R随机网络和B-A无标度网络.振子的初始相位的大小为随机.振子的本征频率符合均值为0、标准差为1的高斯分布,本征频率的大小与节点度没有关系.这里,领导者本征频率ω0=0.5.为了确保网络在没有领导者作用的情况下能达到全网相互同步,数值模拟中耦合强度为100.使用龙格库塔算法进行动力学方程的计算.在数值模拟中系统运行了足够长的时间后,抛去暂态,对稳态的一段时间内的结果取平均值.数值模拟步骤如下:
步骤1 设定复杂系统的振子本征频率和网络结构;
步骤2 设定领导者本征频率,选择节点施加驱动,根据系统耦合强度区间和单位增量,或领导者驱动强度区间和单位增量确定数值模拟轮数;
步骤3 根据数值模拟轮数确定领导者驱动强度,进行这一系统耦合强度或领导者驱动强度下的系统动力学数值模拟,在系统运行足够长的时间后,抛去暂态,记录稳态;
步骤4 重新设定复杂系统的振子本征频率和网络结构与步骤1中的数值相同;
步骤5 重复步骤3和4,直到系统耦合强度或领导者驱动强度达到设定的最大值.
首先,领导者对所有节点上的振子施加驱动.序参量在系统达到相互同步和驱动同步时都会接近于1,故为了刻画这2种同步的区别和转变,除了系统达到稳态后的序参量r,还计算了当系统处于稳态的一段时间内的集体运动的有效频率⟨dψ/dt⟩.系统的有效序参量和集体运动的有效频率与领导者驱动强度的关系如图1所示.图1中:星形标志线为系统的有效序参量随驱动强度的变化;圆形标志线为系统的集体运动的有效频率随驱动强度的变化;E-R随机网络和B-A无标度网络的结果用红色和绿色表示.随着驱动强度的增大,系统的序参量基本维持1.0附近;集体运动的有效频率从0逐渐变化到接近于0.5,这说明系统从相互同步转变为驱动同步,使系统达到驱动同步的领导者驱动强度存在最小值.数值模拟设定的振子本征频率符合高斯分布,根据式(15)和理论结果驱动强度最小值约等于领导者本征频率.图1中使2种系统达到驱动同步的驱动强度最小值均约等于0.5,证明这一理论结果是正确的.

图1 领导者对所有振子施加驱动时数值模拟的结果Fig.1 Numerical simulation results when leader drives all nodes
接着,领导者选择节点上频率权重较大的50%的振子和频率权重较小的50%的振子来施加驱动.系统的有效序参量和集体运动的有效频率与领导者驱动强度的关系如图2和3所示,图中E-R随机网络和B-A无标度网络的结果用红色和绿色表示.随着驱动强度的增大,与图1中驱动所有振子的结果类似,序参量均基本维持在1.0左右,系统的集体运动的有效频率从0逐渐变化到接近于领导者本征频率0.5.根据式(14),驱动频率权重较大的振子比驱动频率权重较小的振子更难以使网络达到全网的驱动同步,因为相比后者领导者需要的驱动强度更大.图2中,随机网络和无标度网络的驱动强度最小值均远大于图3,证明了这一理论结果的正确性.当网络的平均度相同时,无标度网络相比于随机网络度分布差异性更大,大部分节点的度小于平均度,而中心节点的度远大于平均度.因此,同样选择频率权重较大的50%振子,无标度网络振子的频率权重更小,系统达到驱动同步需要的驱动强度更大.选择频率权重较小的50%振子,无标度网络振子的频率权重更大,系统达到驱动同步需要的驱动强度更小.图2中,无标度网络对应的驱动强度最小值比随机网络的大,而图3中的则小,证明了这一理论结果.
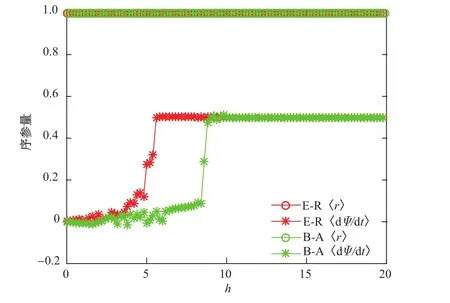
图2 领导者对频率权重较大的50%振子施加驱动时数值模拟的结果Fig.2 Numerical simulation results when leader drives 50%nodes that have larger frequency-weights
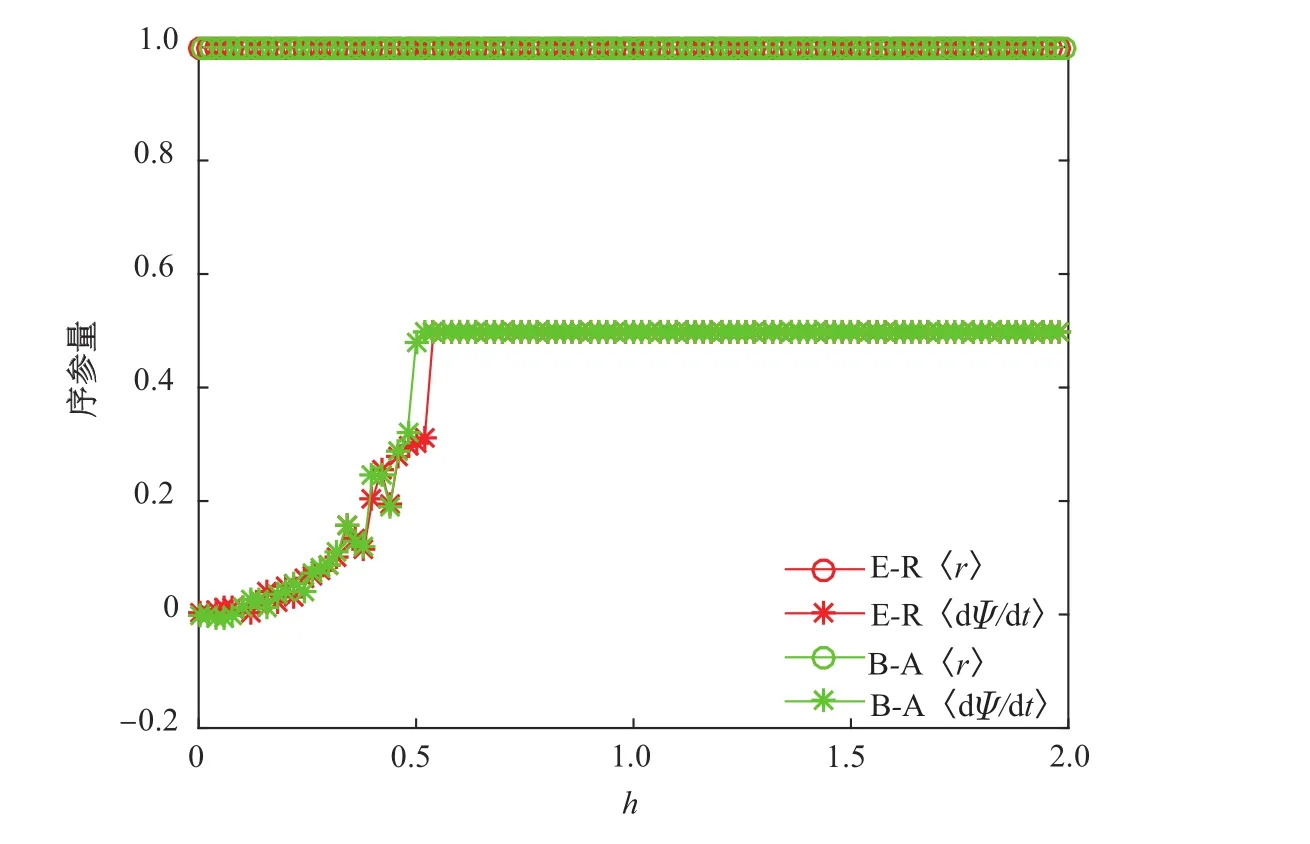
图3 领导者对频率权重较小的50%振子施加驱动时数值模拟的结果Fig.3 Numerical simulation results when leader drives 50%nodes that have smaller frequencyweights
4 总结与展望
本工作研究了由Kuramoto振子组成的频率权重耦合复杂系统受外界领导者节点的驱动时,系统的同步这一重要的集体动力学行为.领导者驱动强度超过一定值就能使系统从相互同步转变为驱动同步,这个领导者驱动强度的最小值与领导者本征频率以及被驱动的振子的数量和频率权重有关.驱动的振子数量越多,振子的频率权重越小,这个领导者驱动强度的最小值越小,更易使网络达到全网的驱动同步.仿真结果证明了本工作结果的正确性,这对于研究现实世界中的复杂系统的同步控制有着重要的意义.今后的研究将关注更多的网络拓扑结构的系统在领导者驱动下的同步.

