基于博弈的私营-公有混合路网定价
江 楠,郑 煜, 张小宁
(1.中国人民银行杭州中心支行,杭州310001;2.同济大学经济与管理学院,上海200092)
在传统的道路拥挤收费的研究中,一般假设整个网络由一个中央管理者实施.然而在实际情况下,交通网络的运营管理者却不唯一.道路私有化模式的兴起造成了道路网络隶属于不同运营者的情况.私有化的道路运营者着眼于最大化自身利润,当市场中存在多个私有运营者时,竞争将不可避免地发生.同样,这种竞争也是传统的道路收费模式无法表达的.
当人们意识到道路供给与定价的竞争越来越普遍时,相关研究就应运而生. de Vany等[1]较早研究了竞争状态下的道路收费问题;Haurie等[2]则考虑了更加一般的情况,认为网络中存在一些不合作的古诺-纳什(Cournot-Nash,CN)博弈主体,这些博弈主体由出行者组成,其内部是相互合作的,而不同的古诺-纳什博弈主体之间则是完全竞争的关系;Harker[3]研究了同时拥有了用户均衡(user equilibrium,UE)和CN出行者的混合均衡路网的出行行为,并提出和证明了该条件下的网络均衡的存在性和唯一性条件;Yang等[4]证明了UE和CN混合网络上最优匿名收费的存在性;Zhang等[5]考虑了多用户类别多标准混合均衡的统一收费框架,探讨了促使系统最优的匿名均一收费的存在性,并给出了线性的收费集合.
Wang等[6]研究了多区域规划设计交通网络时的博弈行为;Jiang等[7]分析了公有和私营混合交通网络上同时优化道路收费和通行券时的理论方法;肖玲等[8]建立了公共停车场与私营停车场的博弈定价模型;Zhang等[9]分析了交通网络上多区域竞争和合作收费策略.由于这类公有-私营混合路网中不同路段由不同属性的实体所运营,这将使得竞争-合作关系变得更加复杂.目前来看,这种不同属性的运营者之间的博弈是否存在均衡解,对系统是否有影响等问题还缺乏理论研究.同时现有的对收费博弈的研究大多局限于私营企业之间的古诺-纳什博弈,缺乏更多对不同博弈模式的研究和对比.
本工作对“私营-公有”混合路网的收费博弈问题进行了研究并建立了模型,理论推导和研究了以下问题:在由私营企业和公有企业控制的平行路网中,私营-公有企业收费博弈的均衡解的存在性和性质.与此同时我们比较不同博弈模式对社会福利、收费、流量等的影响.
1 平行路网“私营-公有”混合收费博弈
这里,除证明平行路网中“私营-公有”混合收费博弈(混合寡头博弈)的纯策略纳什均衡解的存在性,还将比较寡头收费博弈、混合寡头博弈以及社会最优合作对社会福利、收费等的影响.
1.1 平行路网建模
图1为n路段平行路网示意图.图1中,O-D对1-2之间有n条平行路段,路段集合记为K.对路段i,i∈K的出行时间函数为ti(vi),vi为路段i,i∈K的流量.假设ti(vi)为连续可导且单调递增的凸函数.路段i,i ∈K的收费记为τi,另计为收费向量. 此外,定义B(Q)为出行流量时的边际社会出行收益,为出行量的反函数,N为一个任意集合;假设B(Q)为连续可导的减函数,B′=dB(Q)/dQ<0.
对于用户均衡条件下的交通状态,有


图1 n路段平行路网示意图Fig.1 Diagram of n section parallel road network
对任意2条不同的路段i,j∈K,j̸=i,当2条路段都有流量时,

分别对式(1),(2)求τi的偏导数,有

参考文献[10],由式(3),(4)可得

由于B′<0,>0,故有: ∂vi/∂τi>0,∀i∈ K;∂vj/∂τi>0,∀i,j ∈ K,j ̸=i.
1.2 “私营-公有”完全竞争博弈
假设图1中有m条公有路段,公有路段集合记为P.公有企业对其进行收费的目的是追求社会福利的最大化.路段i/∈P,i∈K为私营路段,私营路段集合记为B,收费的目的是追求自身收入的最大化.
在“私营-公有”混合收费博弈中,路网社会福利为所有出行者的出行收益减去所有出行者的出行成本:
公有路段i,i∈P调节收费τi以达到社会福利的最大化:

对式(7)求τi的偏导数,有

命题1 如果B(Q)是Q的线性函数,且ti(vi)是vi的线性函数,则S是τi,∀i∈P的凹函数.
证明 根据式(6)和命题假设,∂vi/∂τi为小于0的常数,t′i为大于0的常数,根据式(7)对S求τ1的2阶偏导数,得

S求τi的2阶偏导数小于0,因此S为τi的凹函数,得证.
在“私营-公有”混合收费博弈中,私营企业i∈B的收入为

私营企业(i̸=1,i∈N)调节收费τi以达到收入的最大化:

对式(11)求τi的偏导数,有
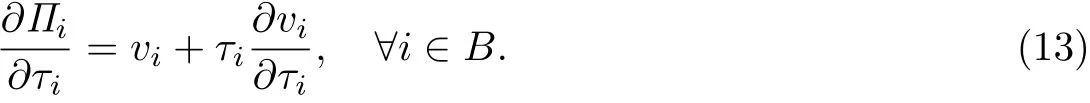
命题2 对τi,i∈B,如果ti(vi)是vi的线性函数,则Πi是τi的凹函数.
证明 根据式(5)和命题假设,∂vi/∂τi是小于0的常数,
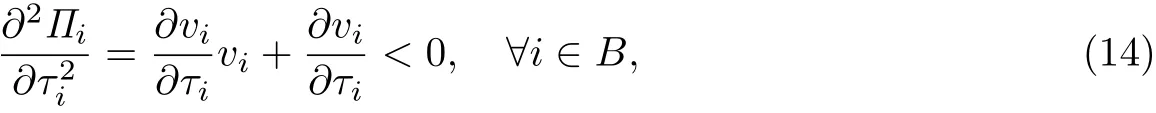
命题3 如果B(Q)是Q的线性函数,且ti(vi),∀i∈N是vi的线性函数,则“私营-公有”混合博弈存在纳什均衡解.
证明 B(Q)是Q的线性函数,且ti(vi),∀i∈N是vi的线性函数,因此命题1和2成立,私营企业和公有企业的目标函数对其决策变量均为凹函数.可见,混合博弈存在纳什均衡解.
根据式(10),对于公有路段i,∀i∈P,有
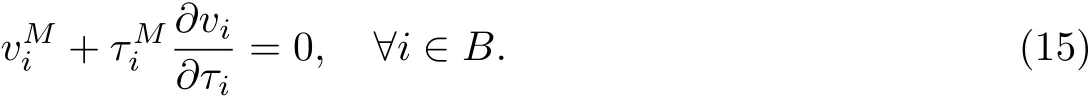
1.3 私营寡头竞争博弈
这里,所有的路段均为私营路段,即B=K,且所有私营路段通过调节自身收费达到自身收入最大化,并与其他私营路段进行竞争,这种竞争称之为私营寡头竞争.市场与经济学中的寡头博弈类似.

在私营寡头竞争博弈中,私营路段(∀i∈K)收入为私营企业(∀i∈K)调节收费τi以达到收入的最大化:

根据命题2和3的论证,如果ti(vi)是vi的线性函数,则寡头博弈存在纳什均衡解.记寡头博弈的纳什均衡解为,此时均衡流量为路网均衡流量为社会福利记为
根据式(15),对于私营路段∀i∈K有

1.4 社会最优合作
在社会最优合作博弈中,一个中央管理者将协同调节所有路段上的收费以达到社会福利的最大化目的:
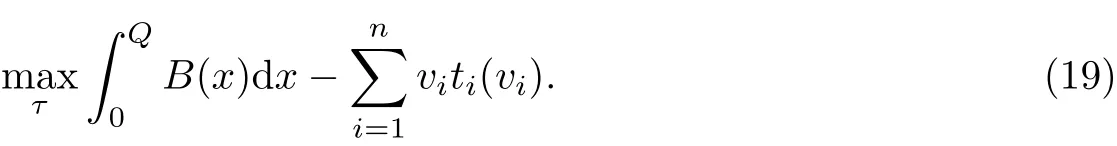
社会最优合作的模型也可以看成是所有路段为公有路段的博弈情形,P=K.
在社会最优合作博弈中,B(Q)可导且单调递减.当ti(vi)为可导递增的凸函数时,路段收费存在路段边际成本定价的解,达到社会福利的最大化[11].

1.5 私营寡头组团竞争模型
假设图1所示的平行路网中存在一个公有运营者,管理了m条路段,公有路段集合记为P.公有企业对其控制的路段进行了收费,目标为社会福利的最大化.另外,n−m条路段为私营路段,私营路段集合记为B,在这里假设所有的私营路段形成联盟,同时与公有企业进行竞争.
在私营寡头竞争博弈中,私营路段联盟的收入为

私营路段联盟通过调节收费τi以达到收入的最大化:

公有企业则通过调节收费τi,∀i∈P以达到社会福利的最大化:

通过命题2和3的论证可得,如果ti(vi)是vi的线性函数,则私营寡头组团竞争博弈存在纳什均衡解.这时记私营寡头组团竞争寡头博弈的纳什均衡解为此时均衡流量为路网均衡流量为社会福利记为SC.
对于私营路段联盟,通过求式(21)对τi的偏导数可得到其最优条件,有
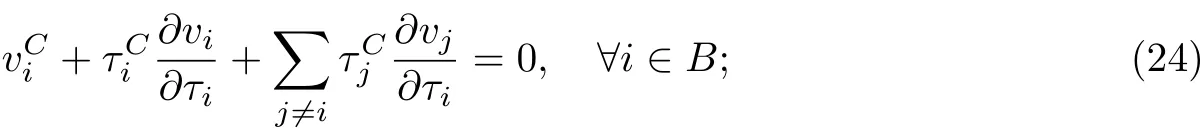
对于公有路段,通过求式(23)对τi的偏导数可得到其最优条件,有

2 不同博弈模式效率对比
引理1 如果B(Q)是Q的线性函数,且ti(vi),∀i∈K是vi的线性函数,则vi可以表达为τi的线性函数.
证明 如果B(Q)是Q的线性函数,且ti(vi),∀i∈K是vi的线性函数,则根据式(5)和(6),对任意路段∀i∈K,vi对任意路段收费的偏导数为常数.因此vi可以表达为τi的线性函数,得证.
特别地,有
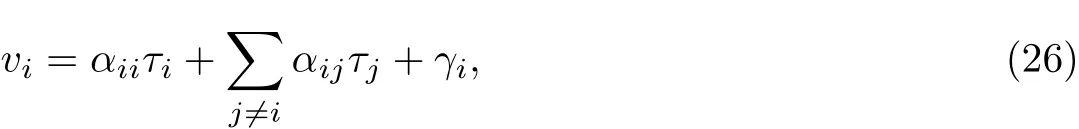
在式(26)中,γi可以看成是路段i,i∈K网络无收费下的纳什均衡流量.
在“私营-公有”完全竞争博弈下,根据式(14),(15)和(26)可以得到混合博弈收费:
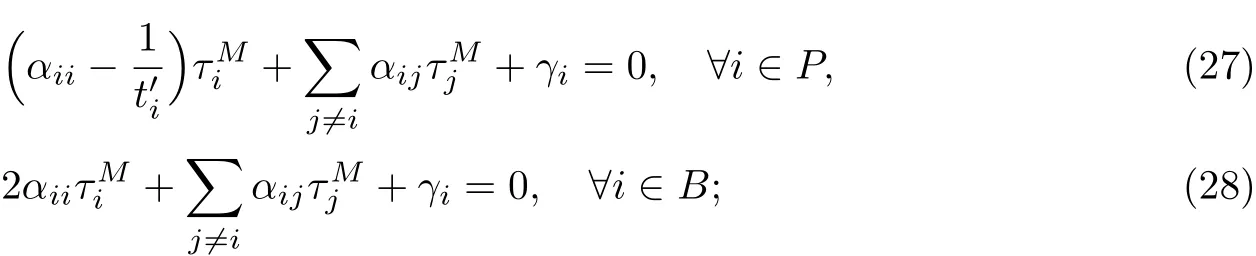
在私营寡头竞争博弈下,根据式(18)和(21)得到了寡头博弈收费:
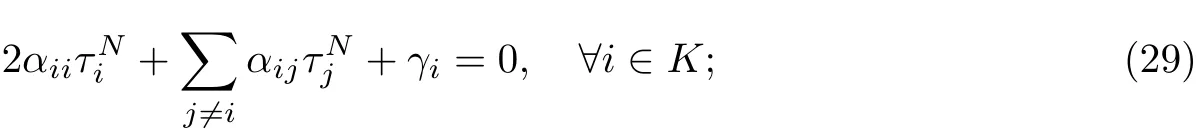
在社会合作博弈下,根据(20)和(26)可以得到如下解集:
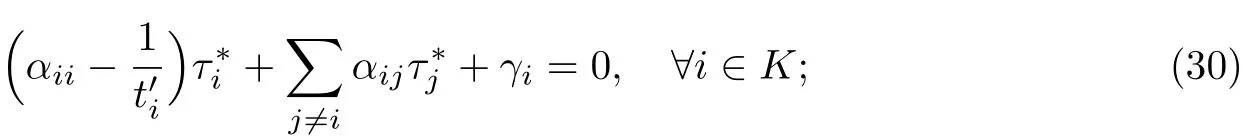
在私营寡头组团博弈下,根据式(24)∼(26)得到了寡头博弈收费:
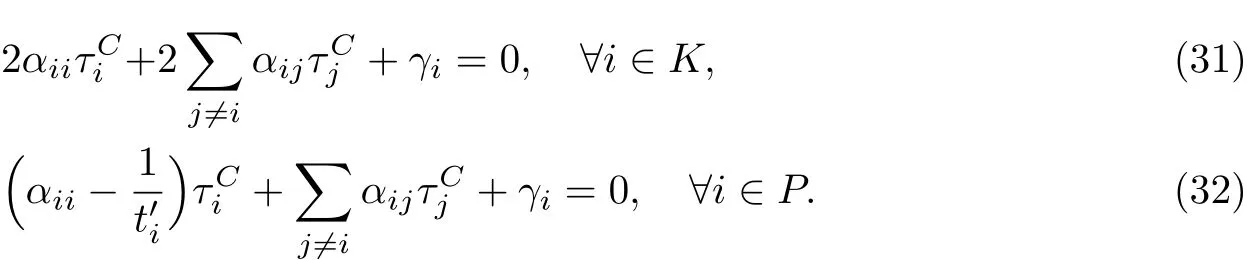
引理2 如果B(Q)是Q的线性函数,且ti(vi),∀i∈K是vi的线性函数,则2αii<0,∀i∈ K.
证明 根据式(5),有
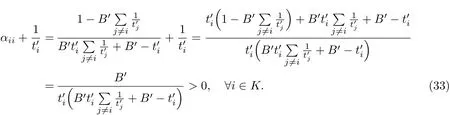
命题4 如果B(Q)是Q的线性函数,且ti(vi),∀i∈K是vi的线性函数,则QN 证明 用反证法证明QN 当∀i∈B时,有 代入式(15)和(18)得 根据QN>QM及式(36)可知,必定存在路段i∈P: 由命题4得 与假设条件中的B(QN) 命题5如果B(Q)是Q的线性函数,且ti(vi),∀i∈K是vi的线性函数,则QM 证明 用反证法证明QM 由于QM>Q∗,故必存在一个 情况1 如果i∈B,则有 将式(15)代入式(40)有 情况2 如果i∈P,则有 由于ti(·)是关于变量的单调递增函数且>0,则有 命题6 如果B(Q)是Q的线性函数,且ti(vi),∀i∈K是vi的线性函数,则 当∀i∈B时,有 代入式(18)和式(24),有 与假设的B(QN)>B(QC)矛盾,因此有QC 命题7 如果B(Q)是Q的线性函数,且ti(vi),∀i∈N是vi的线性函数,则SC 本小节将探讨当平行路网中所有路段是对称时,不同博弈模式的效率.所谓对称路段是指路段的出行时间函数完全相同,故有 对于“私营-公有”完全竞争博弈,根据式˙(15),(16),(43)和(44)我们得到如下平衡条件: 对于私营道路完全竞争博弈,所有路段均为私营路段且由不同公司经营,根据式(18)和(50), 对于私营路段i,∀i∈B,有 当所有路段均为公有路段且只有一个部门管理时,根据式(20),对于每条路段i,∀i∈P,有 对于私营寡头竞争组团博弈,根据对式(24),(25),(43)和(44)求偏导数得到其最优条件 根据式(55),(57)可以看出,公有路段收费的实质是针对本路段进行边际成本收费. 根据式(56),私营路段合作收费可以看成是一个边际成本收费项的收费项,系数可以看成是私营路段联盟的每条路段对其他路段的平均需求溢价系数之和.当路网中私营路段的总数量增加或公有路段数量减少时,系数都会增大,使得私营联盟合作收费增加. 特别地,当路网中路段的数目足够大时可以发现,对于“私营-公有”完全竞争博弈,当路段数量n→∞时有 此时,“私营-公有”完全竞争博弈收费与社会最优的边际成本收费一致. 对于私营寡头竞争博弈,当路段数量n→∞时有 此时“私营-公有”完全竞争博弈收费与社会最优的边际成本收费一致. 对于私营寡头竞争组团博弈,当路段数量n→∞时有 当私营路段数量n−m有限或者公有路段的数量足够大(m→∞)时,有 因此,当路段总数足够大且私营路段数量有限时,“私营-公有”完全竞争博弈收费与社会最优的边际成本收费一致. 本工作证明了在平行路网中,如果路段出行时间函数和反需求函数满足线性条件,则“私营-公有”混合博弈存在均衡解.与此同时,对比混合博弈、寡头博弈和社会最优福利可以发现:寡头博弈下各路段将收取最高的费用,产生最低的总出行流量和社会福利;社会最优福利博弈各路段的收费最低,但是流量和社会福利最高;混合博弈的收费、总出行流量和社会福利介于其他2种博弈之间.此外,当平行路网中的数量足够大时,“私营-公有”完全竞争博弈,对于私营寡头竞争博弈的均衡收费会趋向于边际最优收费,社会福利会趋向于社会最优福利.而对于私营寡头,竞争组团则需要同时满足公有路段和总路段数都足够大时,才能使均衡收费趋向于边际最优收费,社会福利会趋向于社会最优福利.

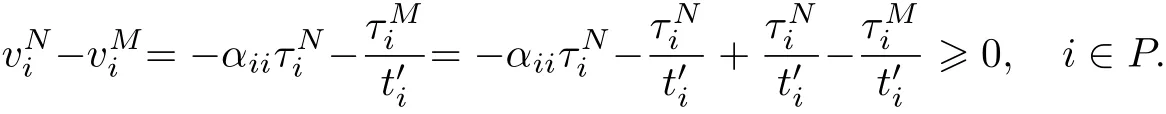


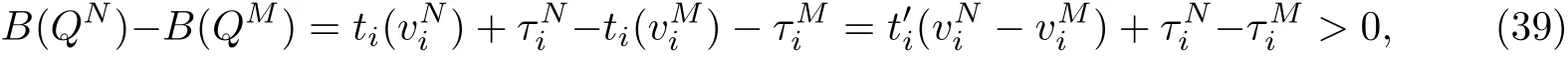
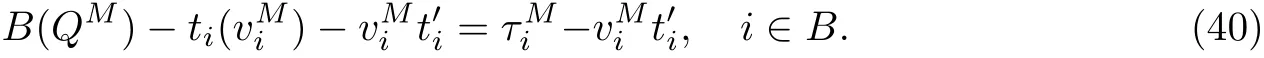
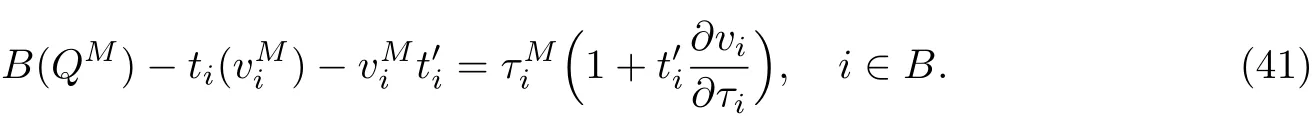

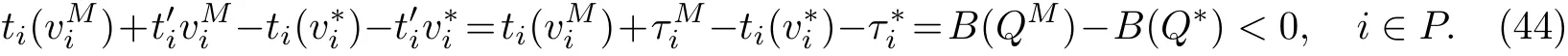


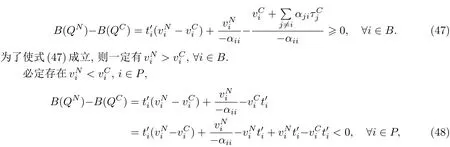
3 算例

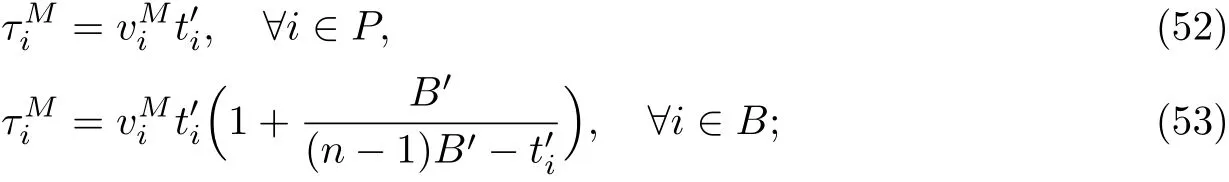



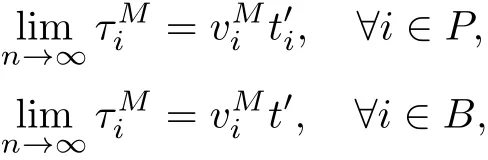
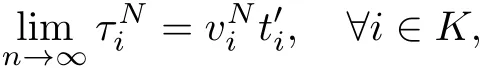


4 结束语

