缺失数据和辅助信息下分位数回归的光滑经验似然
吉肖肖, 张成毅, 罗双华
(1.西安工程大学 理学院, 陕西 西安 710048; 2.西安交通大学 经济与金融学院,陕西 西安 710049)
0 引 言
在抽样调查、临床试验、人口普查、环境监测及生物医学等研究领域, 经常产生大量的缺失数据。缺失数据的统计推断问题已成为研究热点[1-2]。 而在实际的统计推断中, 辅助信息通常可以提高模型的估计效率。 因此, 本文拟讨论响应变量随机缺失和具有辅助信息下的线性分位数回归模型。 模型如下:
Y=XTβ+ε
(1)
式中:Y∈R是响应变量;X=(X1,X2,…,Xd)T∈Rd是d维解释变量;β=(β1,β2,…,βd)T∈Rd是d维未知参数向量;ε是模型的随机误差。 假设{(Xi,Yi,δi),i=1,2,…,n}是模型(1)的一组不完全随机样本, 当δi=1时,Yi有观测值; 当δi=0时,Yi缺失。 假设MAR缺失机制可表示为
P(δi=1|Yi,Xi)=P(δi=1|Xi)=π(Xi)
其中π(x)=P(δ=1|X=x)为选择概率函数。
然而, 变量随机缺失下的线性分位数回归模型在经济学、金融学、医学和生态学等领域应用广泛, 目前已取得了众多研究成果[3-6]。 其中在统计分析领域, 由Owen[7]提出的经验似然方法也已经应用到分位数回归模型中, 但由于其模型的损失函数的势函数不光滑, 所得估计效率并不高。 为了提高估计效率, Whang[8]和Otsu[9]利用光滑方法研究了分位数回归模型的经验似然估计; 李忠桂等[10-11]利用光滑经验似然方法研究了线性分位数回归模型参数的检验问题, 并在此基础上分别用经验似然和光滑经验似然的方法深入研究了右删失数据下分位数回归模型的参数检验问题。当在数据随机缺失的情况下, 李乃医等[12]利用光滑经验似然方法, 讨论了缺失数据下非线性分位数回归模型的回归系数的经验似然置信区域问题; 袁晓惠等[13]在部分协变量随机缺失机制下, 研究了分位数回归参数的诱导光滑加权估计及其渐近协方差估计; Lyu等[14]和Luo等[15]分别用光滑方法讨论了缺失响应数据下部分线性和线性分位数回归模型的经验似然估计。
另外, 在实际的统计推断中, 辅助信息通常可以提高模型的估计效率。 迄今已有大量研究[16-18]。 其中, Tang等[16]首次在正态逼近的基础上, 用经验似然的方法研究了含辅助信息的线性分位数回归模型的估计, 而其方法在进行推理时须估计复杂的协方差矩阵。此外, Horowitz[19]和Whang[8]认为, 标准的Bootstrap理论不能直接推理分位数回归模型的估计。 故在上述研究的基础上, Lyu等[17]提出基于光滑经验似然方法研究辅助信息下分位数回归模型的参数估计问题, 不仅包含了辅助信息, 而且避免了估计复杂的协方差矩阵。 综上, 基于对辅助信息且缺失响应数据下的线性分位数回归模型的统计推断问题还有很多值得讨论。 因此, 本文借助光滑经验似然的方法来研究缺失响应数据和辅助信息下线性分位数回归模型的参数估计, 并在一定条件下讨论所得估计的大样本性质。
1 方法与主要结果
1.1 辅助信息且完全数据下光滑经验似然
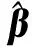
(2)

由于分位数回归的损失函数的势函数不光滑,所得估计的效率并不高。为了提高估计效率,文献[8]给出了缺失数据下分位数光滑经验似然方法。
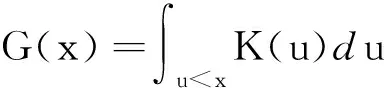
用光滑函数φh(·)近似代替φ(·), 可设β在完全数据下线性分位数回归估计为
在实际的统计推断中, 除用于推断的可观测到样本数据外, 通常还可知样本的一些其他信息。如果可得变量Z的辅助信息, 且存在函数A(·)满足
E{A(Zi)}=0
其中A(Zi)是一个向量函数。通常情况下,使用辅助信息可以改进统计推断,提高参数估计的有效性。
因此, 定义在辅助信息且完全数据下,β线性分位数回归估计为
β分位数光滑经验对数似然比函数为
1.2 辅助信息且加权光滑经验似然
在基于辅助信息且完全数据下的光滑经验似然仅用到了完全观测的数据, 不能充分利用缺失数据下所包含的信息。当缺失概率很大时, 辅助信息下的光滑经验似然所得到的置信域的精度一般相对较低。 为提高置信域的精度, 下面给出基于辅助信息下加权分位数光滑经验似然推断。
首先利用1.1节中的方法, 可设β的加权分位数回归估计为
然而, 在实际问题中, 选择概率函数π(x)通常未知, 需先用核方法去估计选择概率。 Chen等[20]提出了π(x)估计:

其次,定义辅助向量
利用辅助信息定义分位数光滑经验对数似然比函数为
通过Lagrange乘子法,Lwas(β)可表示为
(3)
且λT满足
(4)
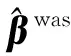
1.3 主要结果
为了方便理论结果,先定义如下必要的矩阵:
D=E(f(0|X)XXT)
定理1假设条件C1)~C6)都成立, 若β是真实参数, 则有

由定理1, 可以构造参数β的置信水平为(1-α)的置信域
Rα={β:Lwas(β)≤Cα}

定理2假设条件C1)~C6)都成立, 则有
2 数值模拟
通过数值模拟验证所提出方法的有限样本性。 现考虑如下模型:
Yi=Xiβ+εi,(i=1,2,…,n)
(5)
式中:协变量X的观测Xi来源于N(0,1)分布;εi来自于均匀分布U(0,1);取β=1。取τ=0.4,0.7,且对于不同的样本量n=100,200,300,基于以下3种选择概率函数分别产生2 000个随机样本:
π3(x)=0.6,x∈R
对以上3种选择概率函数对应的平均缺失率分别约为0.07、0.26和0.40。核函数选择与文献[21]中相同的核函数,即
K(x)=0.75(1-x2)I{|x|≤1}
L(x)=0.5I{|x|≤1}
其中I{·}为示性函数。用最优交叉核实法选择最优窗宽aopt和hopt。交叉核实准则分别为


表 1 置信水平为0.95的置信区间的覆盖概率Tab.1 Coverage probability of confidence interval with a confidence level of 0.95
由表1~2可得如下结论:
1) 在选择概率π1(x),辅助信息且加权分位数光滑经验似然的覆盖概率pwas更高, 但置信区间Lwas更长。 在选择概率π2(x)和π3(x),相比其他方法,辅助信息且加权分位数光滑经验似然的区间长度Lwas较短且覆盖概率pwas较高。 对3种选择概率, 辅助信息且加权分位数光滑经验似然得到的覆盖概率和区间长度和辅助信息且完整数据的分位数光滑经验似然得到的几乎接近, 说明含辅助信息且加权分位数光滑经验似然的效果较好。
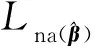
3) 对每一种缺失率, 随着n的增加, 置信区间长度减小而覆盖概率增加。 通常情况下, 当缺失率增加时, 区间长度增加且覆盖概率减小。

表 2 置信水平为0.95的置信区间的平均区间长度Tab.2 Average confidence interval length of confidence interval with a confidence level of 0.95
3 结果证明
设r是一个大于或等于2的整数,g(x)、f(·|x)、F(·|x)分别表示X的密度函数, 在Xi=x条件下ε的条件密度和条件分布函数。 证明主要结果前, 给出所需要的一些正则化条件:
C1) {Yi,Xi:i=1,2,…,n}是独立且同分布的随机向量。
C2)π(x)和g(x)都几乎有至多个r阶的有界偏导数, 且有infxπ(x)>0。
C3) 假设以下3点成立:
ⅰ)K(·)有界且在[-1,1]上有紧支撑。
ⅱ)L(·)是r阶的核函数, 且存在正常数C1,C2和ρ满足
C1I{‖u‖≤ρ}≤L(u)≤C2I{‖u‖≤ρ}。
ⅲ) 对任意常数Ck≠0,K(·)是r阶核函数, 即有
C4) 带宽参数h满足:当n→∞时,nh2r→0且nh/logn→∞。
C5)P(‖X‖>Mn)=o(n-1/2),其中, 当n→∞时, 0 为证明定理1及定理2,引入以下引理。 引理1设条件C2)、C3)中ⅱ)及C5)成立,则对所有1≤i≤n, O(h2r)+o(n-1/2) 一致成立。 该引理及其证明见文献[20]。 引理2设条件C1)~C6)成立, 则当n→∞时, 有 (6) 将上式的右边泰勒展开得 综上,引理2得证。 引理3设条件C1)~C6)成立, 有 证明由引理2的证明可知 令 则 由条件C4)可得T1=op(1)和T2=op(1)。故 E[A(Zi)A(Zi)T]=E(A(Z)A(Z)T) 由中心极限定理可得到引理3。 引理4在引理1条件下, 有 其中‖·‖表示·的范数。 证明记 参考文献[7]中定理3.2, 可证明 (7) 由引理3知 (8) 由式(7)、(8)及中心极限定理可得 ‖λ‖=Op(n-1/2) 定理1的证明由引理4, 可知 对式(3)泰勒展开得 (9) 由式(4)可知 计算可得 (10) 利用式(9)、(10)可得 利用引理3即可证明定理1。 定理2的证明令 其中 对分块矩阵进行简单的计算可得 利用引理3可知 利用光滑经验似然的方法研究在具有辅助信息和缺失响应数据下分位数回归模型的参数估计问题。 其方法不仅包含了缺失数据和辅助信息, 而且又可以在不估计复杂渐近协方差矩阵的情况下研究分位数回归模型的光滑经验似然估计, 并且在一定条件下证明了所得估计的大样本性质。

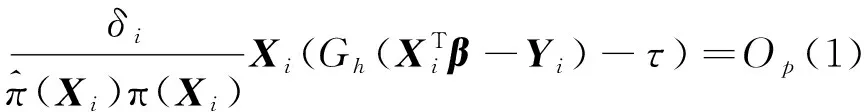


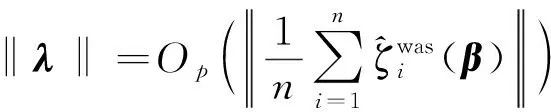

4 结 语

